LOJ2722 「NOI2018」情报中心

「NOI2018」情报中心

题目描述

C 国和D 国近年来战火纷飞。

最近，C 国成功地渗透进入了D 国的一个城市。这个城市可以抽象成一张有$n$ 个节点，节点之间由$n - 1$ 条双向的边连接的无向图，使得任意两个点之间可以互相到达，也就是说这张无向图实际上是一棵树。

经过侦查，C 国情报部部长GGB 惊讶地发现，这座看起来不起眼的城市竟然是D
国的军事中心。因此GGB 决定在这个城市内设立情报机构。情报专家TAC 在侦查后，安排了$m$ 种设立情报机构的方案。这些方案中，第$i$ 种方案是在节点$x_i$ 到节点$y_i$ 的最短路径的所有边上安排情报人员收集情报，这种方案需要花费$v_i$ 元的代价。

但是，由于人手不足，GGB 只能安排上述 $m$ 种方案中的两种进行实施。同时 TAC指出，为了让这两个情报机构可以更好的合作，它们收集情报的范围应至少有一条公共的边。为了评估一种方案的性能，GGB 和 TAC 对所有的边进行了勘察，给每一条边制定了一个情报价值$c_i$，表示收集这条边上的情报能够带来$c_i$ 元的收益。注意，情报是唯一的，因此当一条边的情报被两个情报机构收集时，也同样只会有$c_i$ 的收益。

现在，请你帮GGB 选出两种合法的设立情报机构的方案进行实施，使得这两种方案收集情报的范围至少有一条公共的边，并且在此基础上总收益减去总代价的差最大。

注意，这个值可能是负的，但仍然是合法的。如果无法找到这样的两种方案，请输出$F$。

输入输出格式

输入格式：

从文件center.in 中读入数据。

本题包含多组测试数据。

输入文件的第一行包含一个整数$T$，表示数据组数；

每组数据包含$(n + m + 1)$ 行：

第$1$ 行包含一个整数$n$，表示城市的点数；

第$2$ 到第$n$ 行中，第$(i + 1)$ 行包含三个整数$a_i,b_i,c_i$，表示城市中一条连接节点$a_i$和$b_i$、情报价值为$c_i$ 的双向边，保证$a_i < b_i$ 且$bi$ 互不相同；

第$(n + 1)$ 行包含一个整数$m$，表示TAC 设立的$m$种设立情报机构的方案；

第$(n + 2)$ 到$(n + m + 1)$ 行中，第$(n + i + 1)$ 行包含三个整数$x_i,y_i,v_i$，表示第$i$ 种设立情报机构的方案是在节点$x_i$ 到节点$y_i$ 的最短路径上的所有边上安排情报人员收集情报，并且需要花费$v_i$ 元的代价。

输出格式：

输出文件包含$T$ 行；

对于每组数据，输出一行：如果存在合法的方案，则输出一个整数表示最大的总收
益减去总代价的差；否则输出$F$。

输入输出样例

输入样例#1：
复制

2
5
1 2 1
2 3 3
3 4 2
1 5 8
2
1 4 5
3 5 8
5
1 2 1
2 3 3
3 4 3
1 5 9
2
1 5 5
2 3 8

输出样例#1：
复制

1
F

输入样例#2：
复制

1
11
1 2 2
1 3 0
2 4 1
3 5 7
1 6 0
1 7 1
1 8 1
6 9 3
4 10 2
4 11 8
10
7 10 2
10 7 0
2 11 1
8 6 7
7 7 0
10 1 1
8 2 1
7 8 3
7 7 3
3 9 9

输出样例#2：
复制

13

说明

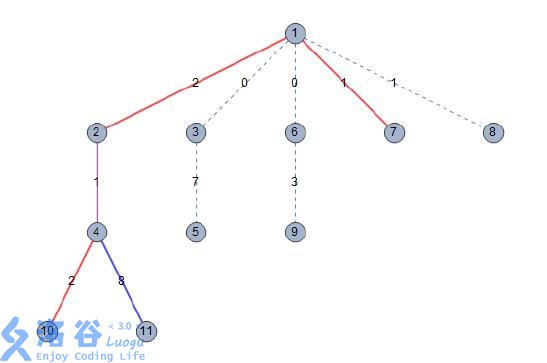
这个样例中包含两组数据。这两组数据的城市相同，只是在情报的价值和情报机构
的方案上有所不同。城市地图如下：

对于第一组数据，方案一中的节点$1$ 到节点$4$ 的最短路径为$1 \rightarrow 2 \rightarrow 3 \rightarrow 4$，方案二中的节点$3$ 到节点$5$ 的最短路径为$3 \rightarrow 2 \rightarrow 1 \rightarrow 5$。选择这两种方案需要花费$5+8 =13$ 的代价，并且每一条边的情报都被收集从而得到$1+3+2+8 = 14$的收益，因此总收益减去总代价为$14 - 13 = 1$。

对于第二组数据，方案一中的节点$1$ 到节点$5$ 的最短路径为$1 \rightarrow 5$，方案二中的节点$2$ 到节点$3$ 的最短路径为$2 \rightarrow 3$。这两种方案收集情报的范围没有公共的边，因此非法，所以这组数据不存在合法方案，应输出$F$。

见选手目录下的center/center2.in 与center/center2.ans。

这个样例只包含一组数据。这一数据中，最优方案为选择第$2$ 种和第$3$ 种方案。

这组数据的城市地图如下，其中加粗的边表示被情报中心收集情报的边，红色的边表示只被第$2$ 种方案的情报中心收集情报的边，蓝色的边表示只被第$3$ 种方案的情报中心收集情报的边，紫色的边表示同时被两个情报中心收集情报的边。

【子任务】

测试点	$n \le$	$m \le$	$T \le 50$	特殊性质
1	$2$	$3$	保证	无
2	$10$	$30$	保证	无
3	$200$	$300$	保证	无
4	$10^3$	$2,000$	保证	$a_i = b_i - 1$
5	$10^4$	$3 \times 10^4$	保证	$a_i = b_i - 1$
6	$5 \times 10^4$	$3 \times 10^4$	保证	$a_i = b_i - 1$
7	$10^4$	$3 \times 10^4$	保证	$c_i=0$
8	$5 \times 10^4$	$10^5$	保证	$c_i=0$
9	$5 \times 10^4$	$10^5$	保证	$c_i=0$
10	$10^4$	$n$	保证	$S_1$
11	$5 \times 10^4$	$n$	不保证	$S_1$
12	$5 \times 10^4$	$n$	不保证	$S_1$
13	$10^4$	$3 \times 10^4$	保证	$S_2$
14	$10^4$	$3 \times 10^4$	保证	$S_2$
15	$5 \times 10^4$	$10^5$	不保证	$S_2$
16	$5 \times 10^4$	$10^5$	不保证	$S_2$
17	$10^4$	$3 \times 10^4$	保证	无
18	$5 \times 10^4$	$ 10^5$	保证	无
19	$5 \times 10^4$	$ 10^5$	不保证	无
20	$5 \times 10^4$	$ 10^5$	不保证	无

表格中的特殊性质如下：

• 特殊性质 $S_1$：对于任意 $i, j$，保证 $x_i$ 到 $y_i$ 的最短路径所经过的编号最小的节点不同于 $x_j$ 到 $y_j$ 的最短路径所经过的编号最小的节点；
• 特殊性质 $S_2$：对于任意 $i$，保证 $x_i$ 到 $y_i$ 的最短路径所经过的编号最小的节点为节点 $1$。

对于所有的数据，$1 \le n \le 5 \times 10^4$，$0 \le m \le 10^5$，$0 \le c_i \le 10^9$，$0 \le v_i \le 10^{10} \times n$。每个测试点中，所有 $n$ 的和不会超过 $1, 000, 233$，所有 $m$ 的和不会超过 $2, 000, 233$。

题解

我把WAautomaton的题解，官方题解和网上找到的代码结合起来反复看，总算看懂了这题的做法。

不妨进行分类讨论。

LCA 两两不同 \((S_{1})\)

首先，如果两条链的 LCA 不是同一个点，那么形成的图应该长这样：



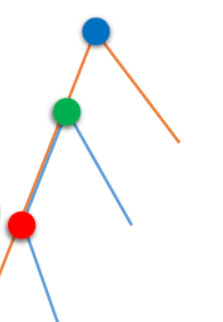
这张图看起来很直观，但是条件是很严格的。具体在 红点不带权深度 > 绿点的不带权深度 > 蓝点的不带权深度 ，且链在红点下方的部分必须分属两个不同的子树。这是为了保证LCA两两不同，有交集，且答案贡献计算式正确。

它对答案的贡献应该是：\(两条链的长度和 − 红点深度 +\max(绿点深度,蓝点深度) − 两条链的费用\)。

于是我们枚举红点，不妨设\(f(i,j)\)表示链一头在\(i\)子树（含\(i\)）里且 LCA的不带权深度 为\(j\)的所有链中，长度 − 费用 最大的，\(g(i,j)\)表示 长度 − 费用 + LCA带权深度 最大的。为什么这么设状态？怎么更新答案呢？请看后文。

那么可以线段树维护这个数组，下标表示 不带权深度 。然后在线段树单点修改以及合并的时候顺带更新答案，这时要遵循左右法^[1]。左右法的目的是去掉\(\max(绿点深度,蓝点深度)\)这个求最值括号（如果\(\max\)前是 - 号就非常有必要了），具体做法就是直接用绿点（LCA不带权深度 较大）的\(g\)和蓝点（LCA不带权深度 较小）的\(f\)来更新答案。在线段树里就用下标较小的节点的\(f\)+下标较大的节点的\(g\)来更新答案，此时线段树下标关系就保证了绿点和蓝点的深度关系。这就不难解释为什么有\(f,g\)的区别。

但注意，由于红点是分叉点，更新答案的链必须分属两棵不同的子树，因此要遵循里外法^[2]。里外法即在DFS的过程中，先用已合并的信息和待合并的信息更新答案，再将信息进行合并。

最后注意因为DFS顺序， 红点不带权深度 在减少，所以当一条链的 LCA不带权深度 = 红点不带权深度 不带权深度的时候，要将它从线段树里删掉。出于同样的根本原因，加点的时候必须保证LCA在红点更高处。总复杂度\(O(n\log n)\)

LCA 全部相同 \((S_{2})\)

其次，考虑两个 LCA 相同的情况。那么形成的图应该长这样：



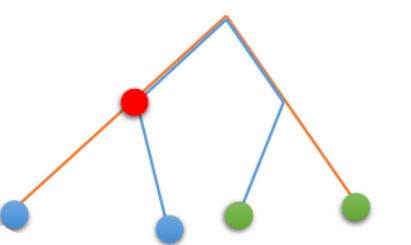
这张图的要求要少一点，只需 红点不带权深度 > LCA不带权深度 和链在红点下方的部分必须分属两个不同的子树就行了。

对于这一部分数据，两条链的交可能不是直上直下的。关键性质 : 链并的两倍 = 两条链长 + 蓝点距离 + 绿点距离

它对答案的贡献应该是：\(\frac{1}{2}(两条链长+蓝点距离+绿点距离−2\times两条链总费用)\)。

考虑枚举红点，我们把 链长 − 2×费用 + 蓝点深度 作为一个绿点的点权，那么我们实际上需要找到红点下分属两个子树中的蓝点，对应绿点的 点权和 + 距离 的最大值。

容易发现，由于边权非负（点权的正负性不需要考虑），那么计算两个集合并的最远点对，端点一定在原来两个集合的最远点对中产生^[3]。于是可以\(O(1)\)合并。

为了能对LCA不同的情况枚举红点我们对于所有LCA相同的链建虚树，直接在虚树上合并最远点对信息并更新答案即可。这部分复杂度在建虚树的 sort 上，\(O(n\log n)\)

因此整个问题也是\(O(n\log n)\)的了。

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
    for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;

co ll INF=1e18;
co int N=2e5+1,LG=19;
int n,dep[N],pos[N],dfn,lg[N];ll dis[N];
pair<int,int> st[N][LG]; // dep and vertice
vector<pair<int,int> > e[N];

void dfs(int x){
	st[pos[x]=++dfn][0]=make_pair(dep[x],x);
	for(unsigned i=0;i<e[x].size();++i){
		int y=e[x][i].first;
		dep[y]=dep[x]+1,dis[y]=dis[x]+e[x][i].second;
		dfs(y);
		st[++dfn][0]=make_pair(dep[x],x);
	}
}
il int lca(int x,int y){
	if(x==y) return x;
	x=pos[x],y=pos[y];
	if(x>y) swap(x,y);
	int k=lg[y-x+1];
	return min(st[x][k],st[y-(1<<k)+1][k]).second;
}
il ll get_dis(int x,int y){
	return dis[x]+dis[y]-2*dis[lca(x,y)];
}

int m;
struct node {int x,y;ll cost;}p[N]; // chain and cost

namespace distinct{
	co int SZ=N*LG;
	int tot,lc[SZ],rc[SZ],root[N];
	pair<ll,ll> val[SZ]={make_pair(-INF,-INF)}; // f,g
	ll res;

	il void get_max(pair<ll,ll>&x,co pair<ll,ll>&y){
		x.first=max(x.first,y.first),x.second=max(x.second,y.second);
	}
	il void pushup(int x){
		val[x]=val[0];
		if(lc[x]) get_max(val[x],val[lc[x]]);
		if(rc[x]) get_max(val[x],val[rc[x]]);
	}
	void modify(int&x,int l,int r,int p,co pair<ll,ll>&v,bool cover=false){
		if(!x) x=++tot,lc[x]=rc[x]=0,val[x]=val[0]; // new node
		if(l==r) return cover?val[x]=v,void():get_max(val[x],v);
		int mid=l+r>>1;
		if(p<=mid){
			modify(lc[x],l,mid,p,v,cover);
			if(rc[x]) res=max(res,v.first+val[rc[x]].second);
		}
		else{
			modify(rc[x],mid+1,r,p,v,cover);
			if(lc[x]) res=max(res,val[lc[x]].first+v.second);
		}
		pushup(x);
	}
	int merge(int x,int y){
		if(!x||!y) return x|y;
		res=max(res,val[lc[x]].first+val[rc[y]].second); // left-right
		res=max(res,val[lc[y]].first+val[rc[x]].second);
		lc[x]=merge(lc[x],lc[y]),rc[x]=merge(rc[x],rc[y]);
		get_max(val[x],val[y]);
		return x;
	}

	vector<int> query[N];
	ll ans;

	void dfs(int x){
		for(unsigned i=0;i<query[x].size();++i){
			int id=query[x][i],lca=::lca(p[id].x,p[id].y);
			if(lca==x) continue; // make sure of intersection
			ll len=get_dis(p[id].x,p[id].y);
			pair<ll,ll> cur=make_pair(len-p[id].cost,len-p[id].cost+dis[lca]);
			res=-INF,modify(root[x],1,n,dep[lca],cur);
			ans=max(ans,res-dis[x]);
		}
		for(unsigned i=0;i<e[x].size();++i){
			int y=e[x][i].first;
			dfs(y);
			res=-INF,root[x]=merge(root[x],root[y]);
			ans=max(ans,res-dis[x]);
		}
		if(dep[x]!=1) modify(root[x],1,n,dep[x]-1,make_pair(-INF,-INF),true); // make sure of intersection
	}
	void main(){
		for(int i=1;i<=m;++i) query[p[i].x].push_back(i),query[p[i].y].push_back(i);
		dfs(1);
	// clear
		tot=0;
		for(int i=1;i<=n;++i) query[i].clear(),root[i]=0;
	}
}

struct far_pair {pair<int,ll> a,b;ll w;};
il bool operator<(co far_pair&x,co far_pair&y){
	return x.w<y.w||x.w==y.w&&!x.a.first;
}

namespace same{
	far_pair best[N]={(far_pair){make_pair(0,0LL),make_pair(0,0LL),-INF}};
	vector<int> has[N],e[N];
	vector<pair<int,ll> > query[N]; // point and value
	ll ans;

	il far_pair F(co pair<int,ll>&a,co pair<int,ll>&b,int cur,bool update=true){
		if(!a.first||!b.first) return (far_pair){!a.first?b:a,!a.first?a:b,-INF};
		far_pair res=(far_pair){a,b,(a.second+b.second+get_dis(a.first,b.first))/2};
		if(update) ans=max(ans,res.w-dis[cur]);
		return res;
	}
	il far_pair merge(co far_pair&x,co far_pair&y,int cur){
		far_pair res=best[0];
		res=max(res,F(x.a,y.a,cur)),res=max(res,F(x.a,y.b,cur)); // in-out
		res=max(res,F(x.b,y.a,cur)),res=max(res,F(x.b,y.b,cur));
		res=max(res,x),res=max(res,y);
		return res;
	}
	void dfs(int x){
		best[x]=best[0];
		for(unsigned i=0;i<query[x].size();++i){
			co pair<int,ll>&p=query[x][i];
			best[x]=merge(best[x],F(p,p,x,false),x);
		}
		for(unsigned i=0;i<e[x].size();++i){
			int y=e[x][i];
			dfs(y);
			best[x]=merge(best[x],best[y],x);
		}
	}

	il bool cmp(int x,int y){
		return pos[x]<pos[y];
	}
	bool vis[N];vector<int> can; // for clear
	il void add_edge(int x,int y){
		if(!vis[x]) vis[x]=1,can.push_back(x);
		if(!vis[y]) vis[y]=1,can.push_back(y);
		e[x].push_back(y);
	}
	int st[N],top;
	void build_tree(vector<int>&a,int o){
		sort(a.begin(),a.end(),cmp);
		a.erase(unique(a.begin(),a.end()),a.end());
		st[top=1]=o;
		for(unsigned i=0;i<a.size();++i){
			int u=a[i];
			if(u==o) continue;
			int p=lca(u,st[top]);
			if(p!=st[top]){
				for(;top>1&&dep[st[top-1]]>dep[p];--top) add_edge(st[top-1],st[top]);
				if(st[top-1]!=p) add_edge(p,st[top]),st[top]=p;
				else add_edge(st[top-1],st[top]),--top;
			}
			st[++top]=u;
		}
		for(;top>1;--top) add_edge(st[top-1],st[top]);
		for(unsigned i=0;i<e[o].size();++i) dfs(e[o][i]);
	// clear
		for(unsigned i=0;i<can.size();++i){
			int u=can[i];
			best[u]=best[0],query[u].clear(),e[u].clear(),vis[u]=0;
		}
		can.clear();
	}
	void main(){
		for(int i=1;i<=m;++i) has[lca(p[i].x,p[i].y)].push_back(i);
		for(int o=1;o<=n;++o)if(has[o].size()>=2){
			vector<int> cur; // for vitual tree
			for(unsigned i=0;i<has[o].size();++i){
				co node&p=::p[has[o][i]];
				cur.push_back(p.x),cur.push_back(p.y);
				query[p.x].push_back(make_pair(p.y,get_dis(p.x,p.y)-p.cost*2+dis[p.x]));
				query[p.y].push_back(make_pair(p.x,get_dis(p.x,p.y)-p.cost*2+dis[p.y]));
			}
			build_tree(cur,o);
		}
	// clear
		for(int i=1;i<=n;++i) has[i].clear();
	}
}

void center(){
	read(n);
	for(int i=1,a,b,c;i<n;++i){
		read(a),read(b),read(c);
		e[a].push_back(make_pair(b,c));
	}
// prepare lca
	dep[1]=1,dfs(1),assert(dfn==2*n-1);
	lg[0]=-1;
	for(int i=1;i<=dfn;++i) lg[i]=lg[i>>1]+1;
	for(int j=1;j<=lg[dfn];++j)
		for(int i=1;i+(1<<j)-1<=dfn;++i) st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);
	read(m);
	for(int i=1;i<=m;++i){
		read(p[i].x),read(p[i].y),read(p[i].cost);
		if(p[i].x==p[i].y) --m,--i;
	}
	distinct::ans=same::ans=-INF;
	distinct::main(),same::main();
	ll ans=max(distinct::ans,same::ans);
	if(ans>-INF/10) printf("%lld\n",ans);
	else puts("F");
// clear
	dfn=0;
	for(int i=1;i<=n;++i) e[i].clear();
}
int main(){
	freopen("center.in","r",stdin),freopen("center.out","w",stdout);
	for(int t=read<int>();t--;) center();
	return 0;
}

foreverpiano的c++11版本的封装良好代码

// 毒瘤2合1
#include <bits/stdc++.h>
#define rep(i, n) for (rint i = 1; i <= (n); i ++)
#define re0(i, n) for (rint i = 0; i < (int) n; i ++)
#define travel(i, u) for (rint i = head[u]; i; i = e[i].nxt)
#define rint register int
using namespace std;

typedef long long lo;

inline char gc() {
	static const int MAXSIZE = 1 << 22;
	static char buf[MAXSIZE], *at = buf, *en = buf;
	if (at == en) en = (at = buf) + fread(buf, 1, MAXSIZE, stdin);
	return at == en ? EOF : *at++;
}
#ifndef LOCAL
#define getchar gc
#endif
template <class T> inline void read(T &x) {
	x = 0; char c = getchar(); int f = 0;
	for (; c < '0' || c > '9'; f |= c == '-', c = getchar());
	for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = getchar());
	if (f) x = -x;
}

template <class T> inline void chkmax(T &x, T y) { x = max(x, y); }
template <class T> inline void chkmin(T &x, T y) { x = min(x, y); }

#define int long long
#define mp make_pair
const int inf = 1e18;
const int M = 4e5 + 233;
const int N = 2e5 + 233;
const int lgN = 19;

struct node_t {
	int x, y, cost;
	node_t (int x = 0, int y = 0, int cost = 0) : x(x), y(y), cost(cost) {}
};

struct myPair {
	node_t a, b; int w;
	myPair (node_t a = node_t(), node_t b = node_t(), int w = -inf) : a(a), b(b), w(w) {}
	friend bool operator < (myPair x, myPair y) { return x.w < y.w || x.w == y.w && !x.a.x; }
};

struct E {
	int nxt, to, w;
};

E e[M];
node_t p[N];
int head[N], e_cnt = 0;
pair <int, int> st[N], ff[N][lgN + 2];
int idx, pos[N], dfn[N], clk, dep[N], dd[N], lg[N], fa[N];
int n, m;

inline void replace() {
	re0 (i, 2 * n + 1) {
		head[i] = 0; st[i] = mp(0, 0);
		pos[i] = dfn[i] = dep[i] = dd[i] = lg[i] = fa[i] = 0;
		memset(ff[i], 0, sizeof ff[i]);
	}
	idx = clk = e_cnt = 0;
}

inline void adde(int x, int y, int w) {
	e[++e_cnt] = (E) {head[x], y, w}; head[x] = e_cnt;
}

inline void dfs(int u, int fat) {
	st[pos[u] = ++idx] = mp(dep[u], u);
	dfn[u] = ++clk;
	travel (i, u) {
		int v = e[i].to;
		if (v != fat) {
			fa[v] = u;
			dep[v] = dep[u] + 1;
			dd[v] = dd[u] + e[i].w;
			dfs(v, u);
			st[++idx] = mp(dep[u], u);
		}
	}
}

inline int LCA(int x, int y) {
	if (x == y) return x;
	x = pos[x]; y = pos[y];
	if (x > y) swap(x, y);
	int d = lg[y - x + 1];
	return min(ff[x][d], ff[y - (1 << d) + 1][d]).second;
}

inline void prepare_lca() {
	int up = 2 * n;
	lg[0] = -1;
	rep (i, up) lg[i] = lg[i >> 1] + 1;
	dep[1] = 1;
	dfs(1, 0);
	rep (i, idx) ff[i][0] = st[i];
	rep (j, lgN) for (int i = 1; i + (1 << j) <= idx; i++)
		ff[i][j] = min(ff[i][j - 1], ff[i + (1 << (j - 1))][j - 1]);
}

inline int dist(int x, int y) {
	return dd[x] + dd[y] - 2 * dd[LCA(x, y)];
}

#define P pair <int, int>
namespace same {
#define mid (l + (r - l) / 2)
	const int SZ = N * lgN;
	int tot, L[SZ], R[SZ], ans, res;
	pair <int, int> val[SZ];
	vector <int> vec[N]; int rt[N];

	struct Initer {
		Initer() { val[0] = mp(-inf, -inf); }
	} haha;

	inline void replace() {
		val[0] = mp(-inf, -inf); L[0] = R[0] = 0;
		rep (i, n) vec[i].clear(), rt[i] = 0;
		tot = 0; ans = res = -inf;
	}

	inline void getmax(P &x, P y) {
		chkmax(x.first, y.first);
		chkmax(x.second, y.second);
	}

	inline void ps(int rt) {
		val[rt] = mp(-inf, -inf);
		if (L[rt]) getmax(val[rt], val[L[rt]]);
		if (R[rt]) getmax(val[rt], val[R[rt]]);
	}

	inline void modify(int &rt, int l, int r, int x, P y, bool cover = false) {
		int pre = rt; rt = ++tot;
		L[rt] = L[pre]; R[rt] = R[pre]; val[rt] = val[pre];
		if (l == r) return cover ? val[rt] = y, void() : getmax(val[rt], y);
		if (x <= mid) {
			modify(L[rt], l, mid, x, y, cover);
			if (R[rt]) chkmax(res, y.first + val[R[rt]].second);
		}
		else {
			modify(R[rt], mid + 1, r, x, y, cover);
			if (L[rt]) chkmax(res, val[L[rt]].first + y.second);
		}
		ps(rt);
	}

	inline int make(int x, int y) {
		if (!x || !y) return x | y;
		int p = x;
		chkmax(res, val[L[x]].first + val[R[y]].second);
		chkmax(res, val[L[y]].first + val[R[x]].second);
		L[p] = make(L[x], L[y]);
		R[p] = make(R[x], R[y]);
		getmax(val[p], val[y]);
		return p;
	}

	inline void dfs(int u, int fat) {
		for (int i : vec[u]) {
			int q = LCA(p[i].x, p[i].y);
			int len = dist(p[i].x, p[i].y);
			if (q == u) continue;
			pair <int, int> cur = mp(len - p[i].cost, len - p[i].cost + dd[q]);
			res = -inf;
			modify(rt[u], 1, n, dep[q], cur);
			chkmax(ans, res - dd[u]);
		}
		travel (i, u) {
			int v = e[i].to;
			if (v != fat) {
				dfs(v, u);
				res = -inf;
				rt[u] = make(rt[u], rt[v]);
				chkmax(ans, res - dd[u]);
			}
		}
		if (dep[u] != 1)
			modify(rt[u], 1, n, dep[u] - 1, mp(-inf, -inf), true);

	}

	inline void realmain() {
		rep (i, m) {
			vec[p[i].x].push_back(i);
			vec[p[i].y].push_back(i);
		}
		dfs(1, 0);
	}

#undef mid
}

namespace distinct {
	myPair best[N];
	vector <int> has[N], G[N];
	vector <node_t> query[N];
	int ans;
	int st[N], top = 0;

	inline void replace() {
		top = 0; ans = -inf;
		rep (i, n) has[i].clear();
	}

	inline myPair F(node_t a, node_t b, int cur, bool update = true) {
		if (!a.y || !b.y) return myPair(!a.y ? b : a);
		myPair ret = myPair(a, b, (a.cost + b.cost + dist(a.y, b.y)) / 2);
		if (update)
			chkmax(ans, ret.w - dd[cur]);
		return ret;
	}

	inline myPair make(myPair x, myPair y, int cur, bool update = true) {
		myPair p;
		chkmax(p, F(x.a, y.a, cur));
		chkmax(p, F(x.a, y.b, cur));
		chkmax(p, F(x.b, y.a, cur));
		chkmax(p, F(x.b, y.b, cur));
		chkmax(p, x);
		chkmax(p, y);
		return p;
	}
	int vis[N]; vector <int> cc;
	inline void link(int x, int y) {
		if (!vis[x]) vis[x] = true, cc.push_back(x);
		if (!vis[y]) vis[y] = true, cc.push_back(y);
		G[x].push_back(y);
	}

	inline void dfs(int u) {
		best[u] = myPair();
		for (auto p : query[u]) {
			best[u] = make(best[u], F(p, p, u, false), u);
		}
		for (auto v : G[u])
			dfs(v), best[u] = make(best[u], best[v], u);
	}

	inline void buildTree(vector <int> &a, int o) {
		a.push_back(o);
		sort(a.begin(), a.end(), [] (int x, int y) {
				return dfn[x] < dfn[y];
			});
		a.erase(unique(a.begin(), a.end()), a.end());
		st[top = 1] = o;
		for (int u : a) {
			if (u == o) continue;
			int p = LCA(u, st[top]);
			if (p != st[top]) {
				while (top > 1 && dep[st[top - 1]] > dep[p]) {
					link(st[top - 1], st[top]);
					top--;
				}
				if (st[top - 1] != p) {
					link(p, st[top]);
					st[top] = p;
				} else {
					link(st[top - 1], st[top]);
					top--;
				}
				st[++top] = u;
			} else st[++top] = u;
		}
		while (top > 1) link(st[top - 1], st[top]), --top;
		for (int oo : G[o]) dfs(oo);
		for (int u : cc) {
			best[u] = myPair(); query[u].clear(); G[u].clear();
			vis[u]= false;
		}
		cc.clear();
	}

	inline void realmain() {
		rep (i, m) {
			has[LCA(p[i].x, p[i].y)].push_back(i);
		}
		rep (o, n) if (!has[o].empty()) {
			vector <int> cur;
			for (int i : has[o]) {
				node_t &p = ::p[i];
				cur.push_back(p.x);
				cur.push_back(p.y);
				query[p.x].push_back(node_t(p.x, p.y, dist(p.x, p.y) - p.cost * 2 + dd[p.x]));
				query[p.y].push_back(node_t(p.y, p.x, dist(p.x, p.y) - p.cost * 2 + dd[p.y]));
			}
			buildTree(cur, o);
		}
		rep (i, n) assert(G[i].empty()), assert(query[i].empty());
	}

}

inline void solve() {
	read(n);
	rep (i, n - 1) {
		int x, y, w;
		read(x); read(y); read(w);
		adde(x, y, w); adde(y, x, w);
	}
	prepare_lca();
	int tm; m = 0;
	read(tm);
	rep (i, tm) {
		++m;
		read(p[m].x); read(p[m].y); read(p[m].cost);
		if (dep[p[m].x] < dep[p[m].y]) swap(p[m].x, p[m].y);
		if (p[m].x == p[m].y) --m;
	}
	same::ans = distinct::ans = -inf;
	same::realmain();
	distinct::realmain();
	int ans = max(same::ans, distinct::ans);
	if (ans > -inf / 10) cout << ans << "\n";
	else cout << 'F' << "\n";
	same::replace(); distinct::replace(); replace();
}

signed main(void) {
    int T; for (read(T); T--; solve());
}

---

1. [POI2011]Tree Rotations（BZOJ2212） ↩︎

2. 随便一个计数的树形DP ↩︎

3. 树上的最远点对（51Nod1766） ↩︎