北航oo作业第一单元小结

前言

　　在经过了三次艰辛的oo作业后，oo课程的第一单元告一段落，这一单元，我作为一个oo小白，开始了解oo的编程思想，也有了自己的一点心得体会。把笔粗成字，不当之处，还请各位大佬多多指教。

一.分析程序结构

第一次作业：

　　在第一次作业中，由于刚刚开始接触oo的思想，我还不是很了解面向对象的编程方法，还是按照c语言的思路，将deriviation作为main函数，在deriviation中调用number类，完成运算。

　　具体的操作思路，则是使用正则表达式构造出因子与项，通过正则式匹配来得到每一个项，使用求导公式运算，化简则是选择了运用哈希表将次数相同的表达式的次数相加，合并输出。

　　类图如下：

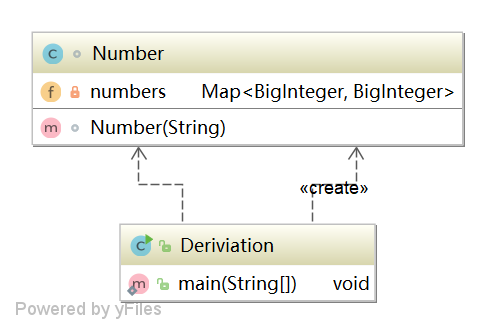
　　复杂度如下：

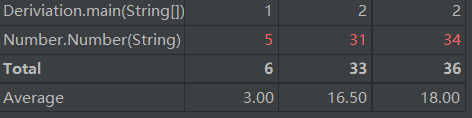
　　可见，我的number复杂度较高，可以进一步优化。

第二次作业：

　　第二次作业由于不涉及因子嵌套，只是添加了三角函数项，我选择了新建一个key类，用来存放三角函数与幂函数的相关次数，并在key类中重构hashcode与equal方法，就可以复用作业一中的hashmap，优化时，加入了，三角函数和为1的特判。

　　下面是类图：

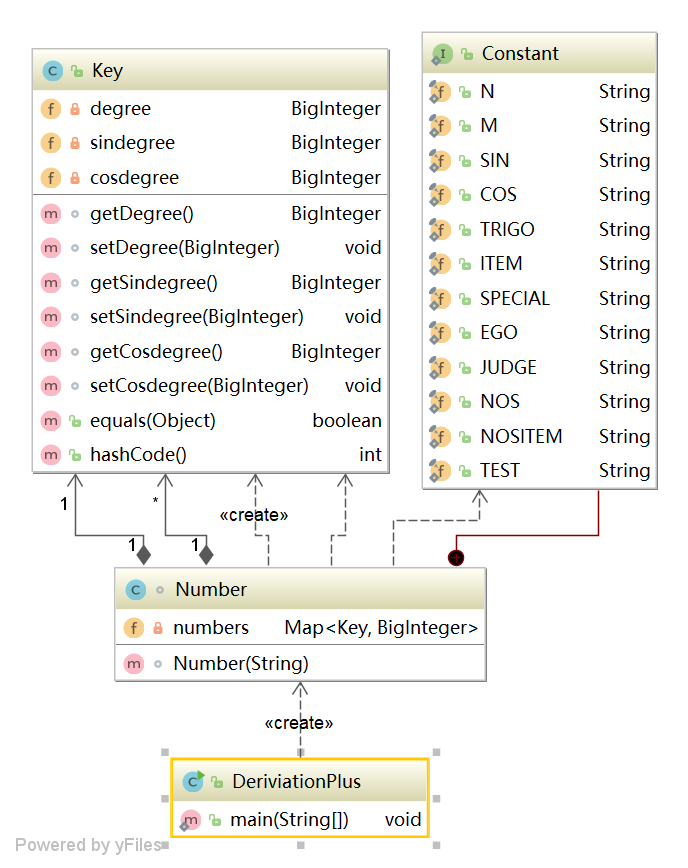
　　复杂度如下：

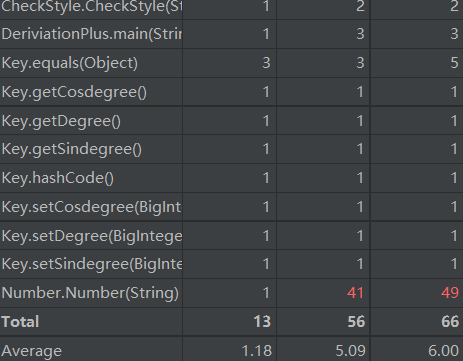
　　由于主要是复用了作业一，导致number的复杂度还是居高不下。

第三次作业：

　　第三次作业加入了嵌套因子，导致正则方法提取失效。我选择了用多个小正则构造来判断输入是否合法。在判断输入合法性时，先进行括号匹配，若有多层括号嵌套，若括号不匹配的话直接判定为非法输出。括号匹配的情况下，逐层判断，每次将当前表达式视为只有一层括号嵌套，递归判断。

　　而在进行求导运算时，这种方法无法准确提取项，便手动根据括号和符号，每次提取出表达式，再将表达式分割为因子，运用链式法则，逐个求导即可。

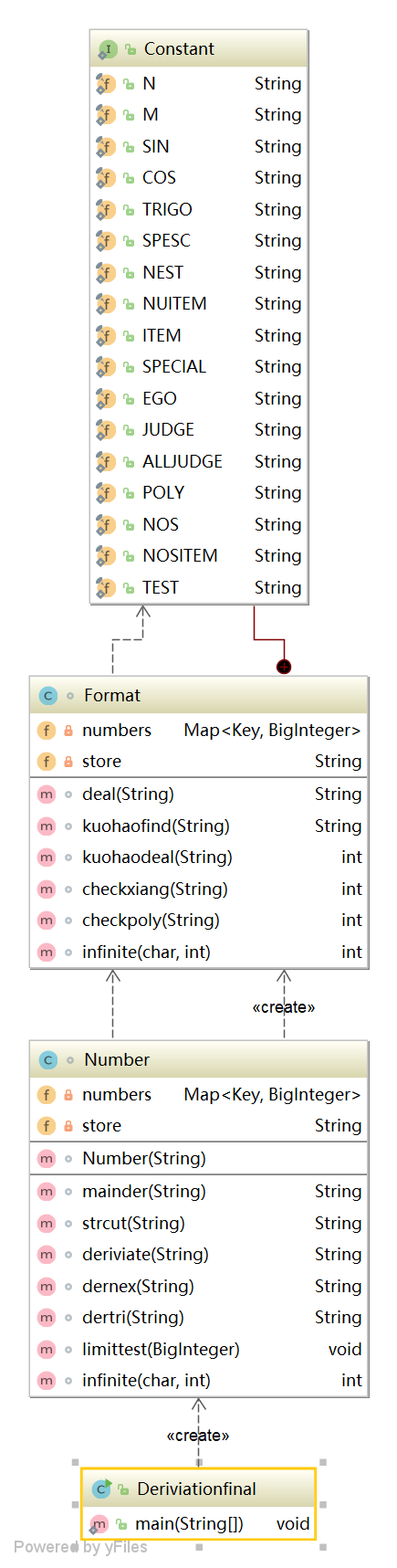
　　类图如下：

　　复杂度如下：

　　

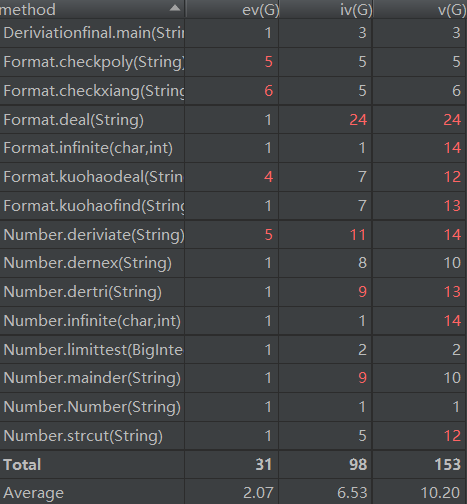
　　由于判断输入合法和求导部分都有大量迭代，复杂度较高。

二.我的bug

　　第一次作业中，我在书写正则表达式的时候，将空格表示为‘ ’，导致可以匹配‘号，此外，没有注意没有符号链接的项，正则匹配也失败。

　　第二次作业中，没有被发现bug。

　　第三次作业中，一个是使用了d{1，5}匹配小于10000的数，忽略了000008这种奇葩。此外，我的递归求导方法，由于嵌套过多，会导致超时。

总而言之，我的代码出现bug集中在正则表达式的构造错误，和求导方法的迭代次数过多。

三.互测的策略

　我的互测策略是尽量先仔细阅读房内同学的代码，争取找到代码逻辑的漏洞，好有的放矢。实在找不到逻辑错误的，会构造测试样例对代码进行黑盒测试。

我结合测试代码结构来构造测试样例，我会观察被测代码的方法结构，思考可能出现的错误点。

四. Applying Creational Pattern

　　　第一二次作业中，我都是将表达式作为对象，进行求导运算。

　　　第三次作业中，由于运算的复杂，在表达式对象的基础上，我又将每一个因子作为对象，进行求导运算。