最长上升子序列问题（O（n^2）算法）

【题目描述】

给定N个数，求这N个数的最长上升子序列的长度。

【样例输入】

7

2 5 3 4 1 7 6

【样例输出】

4

什么是最长上升子序列？ 就是给你一个序列，请你在其中求出一段不断严格上升的部分，它不一定要连续。

就像这样：2,3,4,7和2,3,4,6就是序列2 5 3 4 1 7 6的两种选取方案。最长的长度是4.

什么是最长上升子序列？ 就是给你一个序列，请你在其中求出一段不断严格上升的部分，它不一定要连续。

就像这样：2,3,4,7和2,3,4,6就是序列2 5 3 4 1 7 6的两种选取方案。最长的长度是4.

那么，怎么求出它的最大上升子序列长度为4呢？这里介绍两种方法，都是以动态规划为基础的。

首先，我们先介绍较慢（O（n2n2））的方法。我们记num为到这个数为止，最长上升子序列的长度。

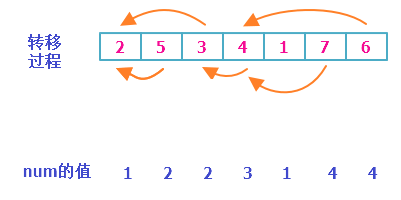
这种方法就是每一次寻找“可以接下去的”，换句话说，设原序列为a，则

当aj<ai(j<i)aj<ai(j<i)且numj+1>numinumj+1>numi时，numi=numj+1numi=numj+1。

对于每一个数，他都是在“可以接下去”的中，从前面的最优值+1转移而来。

因此，这个算法是可以求出正确答案的。复杂度很明显，外层i枚举每个数，内层j枚举目前i的最优值，即O（n^2）。

这是比较简单好理解的方法：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
using namespace std;
int main()
{
	int a[10005];
	int num[10005];
	int n;
	scanf("%d",&n);
	for(int t=0;t<n;t++)
	{
		scanf("%d",&a[t]);
		num[t]=1;
	}
	for(int t=0;t<n;t++)
	for(int j=0;j<t;j++)
	{
		if(a[t]>a[j])
		num[t]=max(num[t],num[j]+1);
	}
	int maxn=-100;
	for(int t=0;t<n;t++)
	{
		maxn=max(num[t],maxn);
	}
	cout<<maxn<<endl;
	return 0;
}