洛谷P2119 魔法阵

P2119 魔法阵

题目描述

六十年一次的魔法战争就要开始了，大魔法师准备从附近的魔法场中汲取魔法能量。

大魔法师有m个魔法物品，编号分别为1,2,...,m。每个物品具有一个魔法值，我们用Xi表示编号为i的物品的魔法值。每个魔法值Xi是不超过n的正整数，可能有多个物品的魔法值相同。

大魔法师认为，当且仅当四个编号为a,b,c,d的魔法物品满足xa<xb<xc<xd，Xb-Xa=2(Xd-Xc)，并且xb-xa<(xc-xb)/3时，这四个魔法物品形成了一个魔法阵，他称这四个魔法物品分别为这个魔法阵的A物品，B物品，C物品，D物品。

现在，大魔法师想要知道，对于每个魔法物品，作为某个魔法阵的A物品出现的次数，作为B物品的次数，作为C物品的次数，和作为D物品的次数。

输入输出格式

输入格式：

输入文件的第一行包含两个空格隔开的正整数n和m。

接下来m行，每行一个正整数，第i+1行的正整数表示Xi，即编号为i的物品的魔法值。

保证1 \le n \le 150001≤n≤15000,1 \le m \le 400001≤m≤40000,1 \le Xi \le n1≤Xi≤n。每个Xi是分别在合法范围内等概率随机生成的。

输出格式：

共输出m行，每行四个整数。第i行的四个整数依次表示编号为i的物品作 为A,B,C,D物品分别出现的次数。

保证标准输出中的每个数都不会超过10^9。

每行相邻的两个数之间用恰好一个空格隔开。

输入输出样例

输入样例#1： 复制

30 8
1
24
7
28
5
29
26
24

输出样例#1： 复制

4 0 0 0
0 0 1 0
0 2 0 0
0 0 1 1
1 3 0 0
0 0 0 2
0 0 2 2
0 0 1 0

输入样例#2： 复制

15 15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

输出样例#2： 复制

5 0 0 0
4 0 0 0
3 5 0 0
2 4 0 0
1 3 0 0
0 2 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 2 1
0 0 3 2
0 0 4 3
0 0 5 4
0 0 0 5

说明

【样例解释1】

共有5个魔法阵，分别为：

物品1,3,7,6，其魔法值分别为1,7,26,29;

物品1,5,2,7，其魔法值分别为1,5,24,26;

物品1,5,7,4，其魔法值分别为1,5,26,28;

物品1,5,8,7，其魔法值分别为1,5,24,26;

物品5,3,4,6，其魔法值分别为5,7,28,29。

以物品5为例，它作为A物品出现了1次，作为B物品出现了3次，没有作为C物品或者D物品出现，所以这一行输出的四个数依次为1,3,0,0。

此外，如果我们将输出看作一个m行4列的矩阵，那么每一列上的m个数之和都应等于魔法阵的总数。所以，如果你的输出不满足这个性质，那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。

【数据规模】

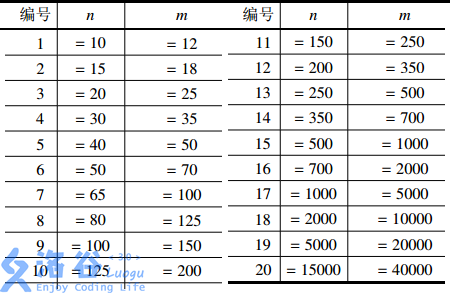
#include<iostream>
#include<cstdio>
#define maxn 40001
using namespace std;
int a1[maxn],a2[maxn],a3[maxn],a4[maxn];
int x[maxn],n,m,w[maxn],nxt[maxn];
int main(){
    freopen("Cola.txt","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++){
        scanf("%d",&x[i]);
        w[x[i]]++;
    }
    int p=,h=;
    for(int i=;i<=n;i++){
        if(w[i]){
            if(h==)h=i;
            nxt[p]=i;
            p=i;
        }
    }
    for(int a=h;a;a=nxt[a]){
        for(int b=nxt[a];b;b=nxt[b]){
            for(int c=nxt[b];c;c=nxt[c]){
                for(int d=nxt[c];d;d=nxt[d]){
                    if((b-a==*(d-c))&&((double)(b-a)<(double)(c-b)/3.0)){
                        a1[a]+=w[b]*w[c]*w[d];
                        a2[b]+=w[a]*w[c]*w[d];
                        a3[c]+=w[a]*w[b]*w[d];
                        a4[d]+=w[a]*w[b]*w[c];
                    }
                }
            }
        }
    }
    for(int i=;i<=m;i++)
        printf("%d %d %d %d\n",a1[x[i]],a2[x[i]],a3[x[i]],a4[x[i]]);
}

65分 暴力

#include<cstdio>
#include<cstring>
const int maxn=;

int x[maxn],w[maxn];
int a[maxn],b[maxn],c[maxn],d[maxn];

int main(){
    int n,m;scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++){
        scanf("%d",&x[i]);
        w[x[i]]++;
    }
    for(int i=;i<=n/;i++){
        int p=i*+,q=;
        for(int j=i*+;j<=n;j++){
            q+=w[j-p]*w[j-p+(i<<)];
            d[j]+=w[j-i]*q;
            c[j-i]+=w[j]*q;
        }
        p=i*+,q=;
        for(int j=n-(i*+);j;j--){
            q+=w[j+p]*w[j+p+i];
            a[j]+=w[j+(i<<)]*q;
            b[j+(i<<)]+=w[j]*q;
        }
    }
    for(int i=;i<=m;i++)
        printf("%d %d %d %d\n",a[x[i]],b[x[i]],c[x[i]],d[x[i]]);
    return ;
}

100分 数学推导