POJ 1183 反正切函数的应用

H - 反正切函数的应用

Time Limit:1000MS     Memory Limit:10000KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

反正切函数可展开成无穷级数，有如下公式

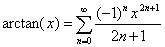(其中0 <= x <= 1) 公式(1)

使用反正切函数计算PI是一种常用的方法。例如，最简单的计算PI的方法：

PI=4arctan(1)=4(1-1/3+1/5-1/7+1/9-1/11+...) 公式(2)

然而，这种方法的效率很低，但我们可以根据角度和的正切函数公式：

tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)*tan(b)] 公式(3)

通过简单的变换得到：

arctan(p)+arctan(q)=arctan[(p+q)/(1-pq)] 公式(4)

利用这个公式，令p=1/2,q=1/3，则(p+q)/(1-pq)=1，有

arctan(1/2)+arctan(1/3)=arctan[(1/2+1/3)/(1-1/2*1/3)]=arctan(1)

使用1/2和1/3的反正切来计算arctan(1)，速度就快多了。

我们将公式(4)写成如下形式

arctan(1/a)=arctan(1/b)+arctan(1/c)

其中a,b和c均为正整数。

我们的问题是：对于每一个给定的a（1 <= a <= 60000），求b＋c的值。我们保证对于任意的a都存在整数解。如果有多个解，要求你给出b+c最小的解。

Input

输入文件中只有一个正整数a，其中 1 <= a <= 60000。

Output

输出文件中只有一个整数，为 b+c 的值。

 

算法分体：就是推导，推到极其复杂啊！

 

代码：

#include <stdio.h>
#include <string.h>
 
int main()
{
	long long a, m, n, dd;
	while(scanf("%lld", &a)!=EOF)
	{
	dd=a*a+1;
 
	for(m=a; m>=1; m--)
	{
		if(dd%m==0)
		{
			break;
		}
	}
	n=dd/m;
	printf("%ld\n", 2*a+m+n );
	}
	return 0;
}

这是一位同胞的解释！可供参考！