机器学习（二十三）— L0、L1、L2正则化区别

1、概念 

　　L0正则化的值是模型参数中非零参数的个数。

　　L1正则化表示各个参数绝对值之和。

　　L2正则化标识各个参数的平方的和的开方值。

2、问题 

　　1）实现参数的稀疏有什么好处吗？

　　一个好处是可以简化模型，避免过拟合。因为一个模型中真正重要的参数可能并不多，如果考虑所有的参数起作用，那么对训练数据可以预测的很好，但是对测试数据就只能呵呵了。另一个好处是参数变少可以使整个模型获得更好的可解释性。

　　2）参数值越小代表模型越简单吗？

　　是的。为什么参数越小，说明模型越简单呢，这是因为越复杂的模型，越是会尝试对所有的样本进行拟合，甚至包括一些异常样本点，这就容易造成在较小的区间里预测值产生较大的波动，这种较大的波动也反映了在这个区间里的导数很大，而只有较大的参数值才能产生较大的导数。因此复杂的模型，其参数值会比较大，但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』。

3、L0正则化

　　根据上面的讨论，稀疏的参数可以防止过拟合，因此用L0范数（非零参数的个数）来做正则化项是可以防止过拟合的。

从直观上看，利用非零参数的个数，可以很好的来选择特征，实现特征稀疏的效果，具体操作时选择参数非零的特征即可。但因为L0正则化很难求解，是个NP难问题，因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似，比L0容易求解，并且也可以实现稀疏的效果。

4、L1正则化

　　L1正则化在实际中往往替代L0正则化，来防止过拟合。在江湖中也人称Lasso。

　　L1正则化之所以可以防止过拟合，是因为L1范数就是各个参数的绝对值相加得到的，我们前面讨论了，参数值大小和模型复杂度是成正比的。因此复杂的模型，其L1范数就大，最终导致损失函数就大，说明这个模型就不够好。

5、L2正则化

　　L2正则化可以防止过拟合的原因和L1正则化一样，只是形式不太一样。

　　L2范数是各参数的平方和再求平方根，我们让L2范数的正则项最小，可以使W的每个元素都很小，都接近于0。但与L1范数不一样的是，它不会是每个元素为0，而只是接近于0。 
　　越小的参数说明模型越简单，越简单的模型越不容易产生过拟合现象。

　　L2正则化江湖人称Ridge，也称“岭回归”

6、L1和L2对比 
                 

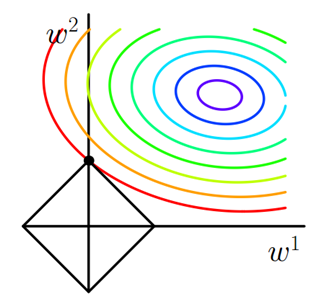
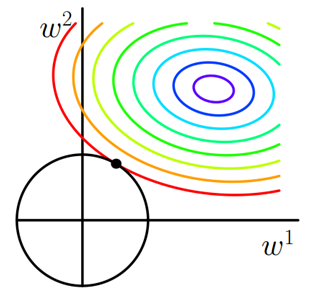
　　可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，有很大的几率等高线会和L1-ball在四个角，也就是坐标轴上相遇，坐标轴上就可以产生稀疏，因为某一维可以表示为0。而等高线与L2-ball在坐标轴上相遇的概率就比较小了。

　　总结： 

　　正则化参数等价于对参数引入 先验分布，使得 模型复杂度 变小（缩小解空间），对于噪声以及 outliers 的鲁棒性增强（泛化能力）。

　　（1）L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。

　　（2）L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择，（在推荐预测点击率时，由于数据的维度可能非常高，L1正则化因为能产生稀疏解，使用的更为广泛一些。）

　　　　  L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合。

　　（3）在所有特征中只有少数特征起重要作用的情况下，选择L1比较合适，因为它能自动选择特征。而如果所有特征中，大部分特征都能起作用，而且起的作用很平均，那么使用L2也许更合适。

　　（4）在面对两个向量之间的差异时，L2比L1更加不能容忍这些差异。也就是说，相对于1个巨大的差异，L2距离更倾向于接受多个中等程度的差异。L1和L2都是在p-norm常用的特殊形式。

　　（5）L1和L2正则先验分别服从什么分布，L1是拉普拉斯分布，L2是高斯分布。