Uva 10375 选择与除法 唯一分解定理

题目链接：https://vjudge.net/contest/156903#problem/E

题意：已知

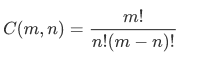
求：C(p,q)/C(r,s)

其中p,q,r,s都是10^4，硬算是肯定超数据类型的。

可以这样处理：利用唯一分解式约分；

首先将所有数，唯一分解；最后，算素数的乘积；

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn = ;
 vector<int> primes;
 int e[maxn];

 bool is_prime(int n) {
     int m = floor(sqrt(n)+0.5); //向下取整
     for(int i=;i<=m;i++)
         if(n%i==) return false;
     return true;
 }

 void add_integer(int n,int d) {
     for(int i=;i<primes.size();i++) {
         while(n%primes[i]==) {
             n /=primes[i];
             e[i]+=d;
         }
         if(n==) break;
     }
 }

 void add_factorial(int n,int d) {
     for(int i=;i<=n;i++)
         add_integer(i,d);
 }

 int main()
 {
     for(int i=;i<=;i++)
         if(is_prime(i)) primes.push_back(i);

     int p,q,r,s;
     while(cin>>p>>q>>r>>s) {
         memset(e,,sizeof(e));
         add_factorial(p,);
         add_factorial(q,-);
         add_factorial(p-q,-);
         add_factorial(r,-);
         add_factorial(s,);
         add_factorial(r-s,);

         double ans = ;
         for(int i=;i<primes.size();i++) {
             ans*=pow(primes[i],e[i]);
         }

         printf("%.5lf\n",ans);

     }

     return ;
 }