Neural Networks and Deep Learning 笔记

1 Introduction to Deep Learning

介绍了神经网络的定义，有监督学习，分析了为什么深度学习会崛起

1.1 结构化数据/非结构化数据

结构化数据：有一个确切的数据库，有key-value索引

非结构化数据：音频、图像等。没有确定的结构

1.2 为什么深度学习会兴起

数据规模、算力提升、算法创新

2 Neural Networks Basics

如何把逻辑回归问题当作一个神经网络，如何使用python，如何向量化

2.1 二分类问题

标签0代表不是猫，标签1代表猫

图片信息展开。例如一个图像尺寸为64*64*3（尺寸，RGB），在当前处理时，需要将其展开为一个12288维向量使用。

2.2 逻辑回归

给定x，希望计算的\(\hat y\)为y=1的概率
\[
\hat y = p(y=1|x)
\]
sigmoid函数
\[
\sigma(z)=\frac{1}{1+e^{-z}}
\]
逻辑回归的输出
\[
\hat y=\sigma(w^Tx+b)
\]

2.3 损失函数和代价函数

loss function，损失函数是衡量算法在单个样本上的表现。

cost function，代价函数时衡量算法在所有训练样本上的表现。

逻辑回归的损失函数见式4和代价函数见式5。

loss function:
\[
L(\hat y,y)=-(ylog(\hat y)+(1-y)log(1-\hat y))
\]
cost function:
\[
J(w,b)=\frac{1}{m}\sum\limits_{i = 1}^m{L(\hat y^{(i)},y^{i})}=\frac{1}{m}\sum\limits_{i = 1}^m{-(ylog(\hat y)+(1-y)log(1-\hat y))}
\]

2.4 如何理解逻辑回归的损失函数

2.4.1 单个样本

已知一个样本(x, y)。模型的\(p(y|x)\)是当输入x时，输出y的概率。通俗讲就是预测正确的概率。因为逻辑回归只有0和1两种情况，所以这个概率公式为式6.
\[
p(y|x)=\hat y^y(1-\hat y)^{(1-y)}
\]
对于上面式子的解释：

当\(y=1\)时，\(1-y\)为0，任何数的0次方都为1，所以\(p(y|x)=\hat y。\)

当\(y=0\)时，\(p(x|y)=(1-\hat y)\)

我们希望能够最大化这个概率，由于log是单调递增函数，所以取log之后最大化，也是这个概率的最大化。加上负号就变成损失函数，最小化损失函数。

2.4.2 m个样本

假设m个样本都是相互独立的，那么对于m个样本都预测正确的概率就为单个样本相乘。
\[
p(所有样本预测正确)=\prod ^ m _{i=1} p(y^{(i)}|x^{(i)})
\]
取log之后，并将右边缩放就是m个样本的损失函数了。

2.5 梯度下降法

每个点计算其梯度，向负梯度方向移动，直到收敛。对于逻辑回归更新如式6和式7。
\[
w:=w-\alpha\frac{\partial J(w,b)}{\partial w}
\]

\[
b:=b-\alpha \frac{\partial J(w,b)}{\partial b}
\]

2.6 导数

回顾微积分基础

2.7 计算图

计算图如下图所示。在神经网络中，计算图中绿色表示了前向传播的过程，红色表示了反向传播的过程。使用计算图可以清楚的解释整个计算过程。

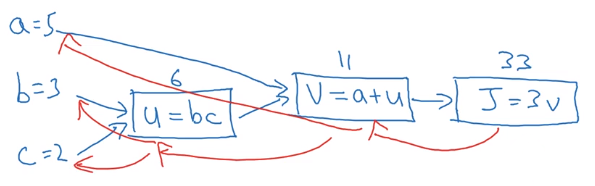
反向传播过程，可以认为是个链式求导过程。求导结果如下图。

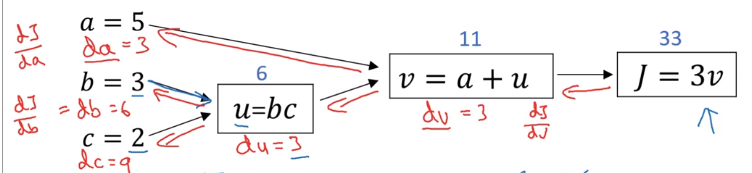
2.8 梯度下降在逻辑回归中的应用

在逻辑回归中应用梯度下降方法的计算图如下。

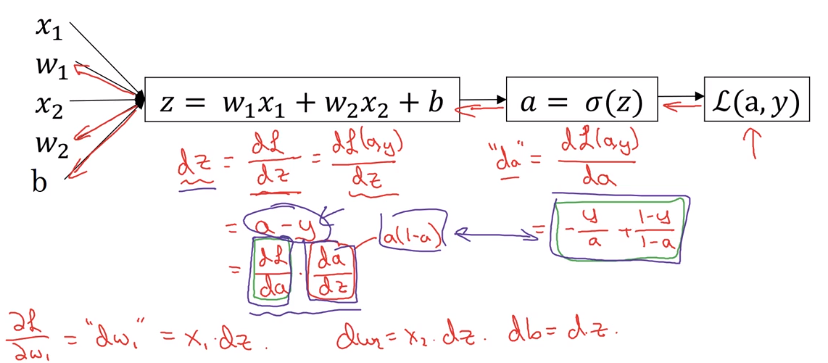
整理为公式，推导很简单，自己推过。
\[
\frac{dL(a,y)}{da}=-\frac{y}{a}+\frac{1-y}{1-a}
\]

\[
\frac{dL}{dz}=\frac{dL}{da}\cdot\frac{da}{dz}=a-y
\]

\[
\frac{dL}{dw_1}=\frac{dL}{dz}\cdot\frac{dz}{dw}=x_1\cdot{dz}
\]

\[
\frac{dL}{dw_2}=\frac{dL}{dz}\cdot\frac{dz}{dw}=x_2\cdot{dz}
\]

\[
\frac{dL}{db}=dz
\]

2.9 拥有m个样本的逻辑回归的梯度下降

注意将J、dw、db这些求和，并除以m

2.10 向量化

在拥有m个样本的计算中，可以将数据向量化，不进行显示的循环操作，加速程序速度。因为cpu/gpu可以并行化计算。

x变为一个\(n_x \times m\)的矩阵，z和\(\hat y\)变为Z和A会变为\(1 \times m\)的矩阵

前向传播公式：
\[
Z=w^TX+b
\]

\[
A=\sigma(Z)
\]

反向传播公式：
\[
J(w,b)=\frac{1}{m}\sum{-(YlogA+(1-Y)log(1-A))}
\]

\[
dZ=A-Y
\]

\[
dw=\frac{1}{m} \cdot X \cdot dZ^T
\]

\[
db=\frac{1}{m} \cdot \sum{dZ}
\]

\[
w:=w-a\cdot dw
\]

\[
b:=b-a \cdot db
\]

2.11 python中的广播

在对于元素的加减乘除中，会将小尺寸的矩阵复制为大尺寸，这里叫做广播。

如果两个矩阵的某个维度长度相符，或其中一方的轴长度为1，则会在上面进行广播。

3 Shallow neural networks

介绍什么是神经网络

3.1 神经网络的表示

输入层、隐藏层、输出层

L表示不包括输入层的层数，l表示第l层。输入层为第0层。

\(a^{[l]}\)表示第l层的输出a代表activation激活。

3.2 前向传播

\[
Z^{[l]}=W^{[l]}A^{[l]}+b^{[l]}
\]

\[
A^{[l]}=g(Z^{[l]})
\]

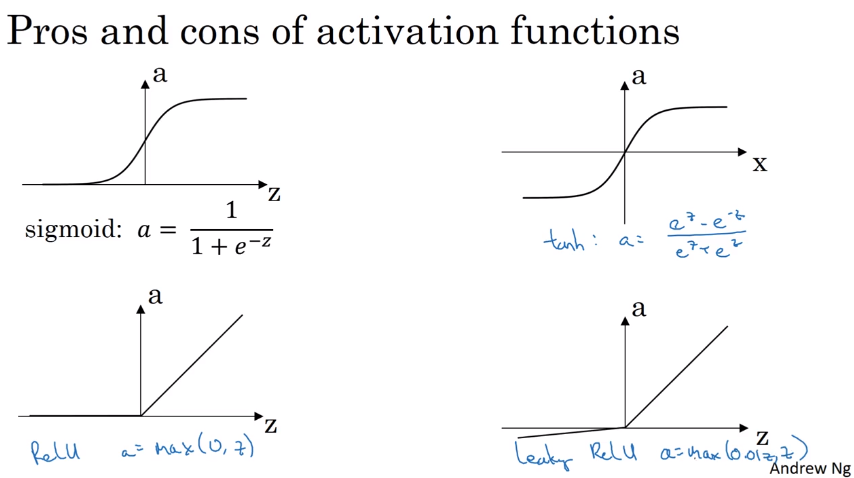
3.3 激活函数

3.3.1 定义

四种激活函数定义如下式。
\[
sigmoid:a=\frac{1}{1+e^{-z}}
\]

\[
tanh:a=\frac{e^z-e^{-z}}{e^z+e^{-z}}
\]

\[
Relu:a=max(0,z)
\]

\[
leaky Relu:a=max(0.01z,z)
\]

四种激活函数如下图。

3.3.2 导数

\[
sigmoid:g(z)'=a(1-a)
\]

\[
tanh:g(z)'=1-(tanh(z))^2
\]

\[
Relu:g(z)'=\left\{ {\begin{array}{*{20}{c}}
0&{z < 0}\\
1&{z \ge 0}
\end{array}} \right.
\]

\[
leaky\ Relu:g(z)'=\left\{ {\begin{array}{*{20}{c}}
0.01&{z < 0}\\
1&{z \ge 0}
\end{array}} \right.
\]

备注：对于relu和leaky relu，在0处的导数未定义，实际使用中归为大于0的情况。

3.3.3 讨论

关于这些函数的结论：

sigmoid：输出层是一个二分类问题时用，其余场合不用

tanh：几乎是和所有场合，因为它可以将输出的平均值大约为0

Relu：最常用的默认函数。相对于sigmoid和tanh，不会出现当数值过大或过小时，梯度很小。

3.3.4为什么使用非线性激活函数

因为使用线性激活函数，那么多层网络可以被简化为一个线性变换。

3.4 神经网络的梯度下降

浅层神经网路进行二分类时的推导。略过了，直接看后面深层的推导吧。

3.5 随机初始化

神经网络权重初始化为0，会造成每一层的每个neuron对应上一层每个元素的权重都相同。既图中W[1]每一行相同，但是每一行的元素并不是相同的。

每行都相同会造成每一层每个neuron的输出都相桶。会造成对称性问题

然而对于逻辑回归，由于只有一个神经元，所以没有这个问题。相当于只有W的其中一行，一行每个元素不是相同的。所以没有问题。

这里我觉得吴恩达老师在第二部分的初始化练习题中给的例子不好。给我造成了一个随机初始化为0将不更新参数的错觉。题目使用了特殊的训练数据造成的，实际上还是会更新参数，但是没法打破对称性问题。具体解释如下。

在这个题目中，神经网络无论怎么更新，参数都为0。由于实验的数据十分特殊，训练集中label=0和lable=1的个数相同，造成在反向传播时计算\(dW^{[3]}=\frac{1}{m}dZ^{[3]}A^{[2]T}=[0]\)。其中\(dZ^{[3]}\)拥有n个正数和n个负数，而且相同。而\(A^{[2]}\)全等于0.5。所以计算出dW全等于0，接下来的更新都等于0。如果数据集不特殊，还是可以更新的，但是就和第一段描述的情况相同了。（最开始还以为relu激活函数造成的，实际并不是）

而对于逻辑回归，不会出现全相同的\(A^{[2]}\)，\(A^{[2]}\)将会是X，X不可能全相同，所以全部初始化为0在特殊情况也不会有影响。

4 Deep Neural Networks

4.1 深层神经网络

就是比浅层神经网络有更多的隐藏层。有一些函数，只有非常深的神经网络能学会。

符号定义：L表示层数，\(n^{[l]}\)表示第l层的节点个数，\(a^{[l]}\)表示l层激活后的结果。

符号含义可以看官方的pdf

4.2 前向传播

向量化之后的式子，这里还需要一个显示的循环，从第一层到第L层
\[
Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}
\]

\[
A^{[l]}=g^{[l]}(Z^{[l]})
\]

前向传播会缓存一些内容：Z、

这里元素的维度需要注意，其中
\[
W^{[l]}、dW^{[l]} : n^{[l]} \times n^{[l]}
\]

\[
b^{[l]}、db^{[l]}:n^{[l]}\times 1
\]

\[
Z^{[l]}、A^{[l]}:n^{[l]}\times m
\]

4.3 反向传播

向量化之后的例子，和前向一样，需要一个显示的循环。而且需要用到前向传播缓存的内容。
\[
dZ^{[l]}=dA^{[l]}*g^{[l]}{'}(Z^{[l]})
\]

\[
dW^{[l]}=\frac{1}{m}dZ^{[l]}A^{[l-1]T}
\]

\[
db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]}, axis = 1, keepdims=True)
\]

\[
dA^{[l-1]}=W^{[l]T}dZ^{[l]}
\]

4.4 为什么使用深层表示

4.4.1 深层网络在计算什么

靠前层的在计算简单的内容，靠后的层计算复杂的内容。

4.4.2 为什么用深层网络

在某些情况下，例如x1-xn的异或运算。如果使用深层网络，节点数只有logn。如果使用浅层网络，需要\(2^{n-1}\)个节点。

吴恩达在这里说深度学习其实应该叫多隐层神经网络，名字被炒作了。

4.5 搭建神经网络块

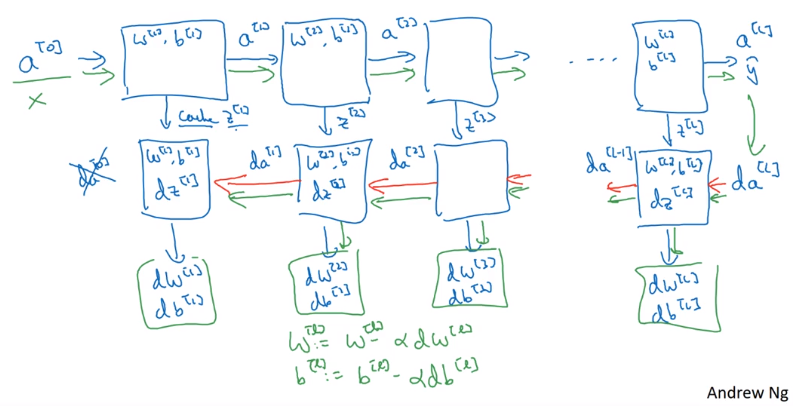
其中的箭头，蓝色的为正向传播，红色的为反向传播，绿色的表示一个训练过程。

4.6 参数和超参数

后面有更仔细的讲解。这里说明一个领域对超参数的直觉不一定适合其他领域。

4.7 神经网络和大脑的关系

神经网络只是一个过度简化的神经元。现在并不能解释清楚一个神经元。这么类比不妥。