c#数字图像处理（七）直方图匹配

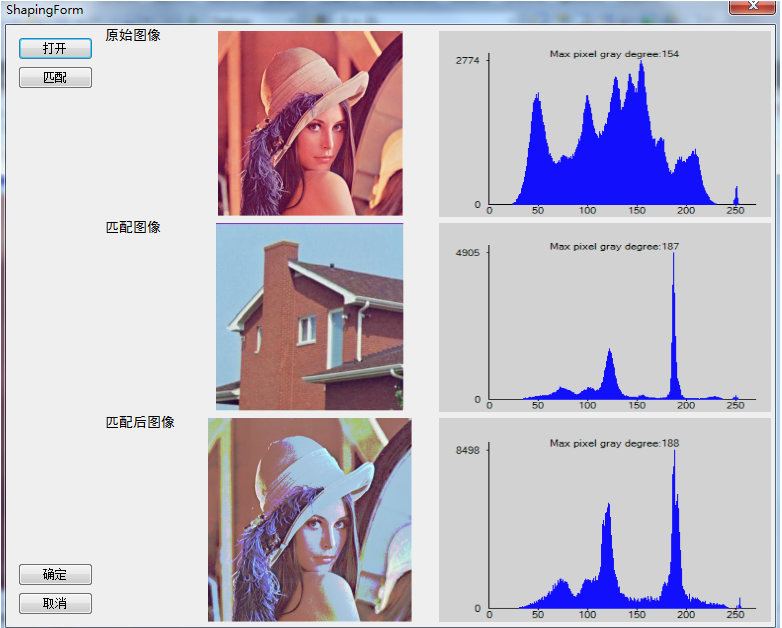
直方图匹配，又称直方图规定化，即变换原图的直方图为规定的某种形式的直方图，从而使两幅图像具有类似的色调和反差。直方图匹配属于非线性点运算。

直方图规定化的原理：对两个直方图都做均衡化，变成相同的归一化的均匀直方图，以此均匀直方图为媒介，再对参考图像做均衡化的逆运算

 　　　　/// <summary>
        /// 直方图匹配
        /// </summary>
        /// <param name="srcBmp">原始图像</param>
        /// <param name="matchingBmp">匹配图像</param>
        /// <param name="dstBmp">处理后图像</param>
        /// <returns>处理成功 true 失败 false</returns>
        public static bool HistogramMatching(Bitmap srcBmp, Bitmap matchingBmp, out Bitmap dstBmp)
        {
            if (srcBmp == null || matchingBmp == null)
            {
                dstBmp = null;
                return false;
            }
            dstBmp = new Bitmap(srcBmp);
            Bitmap tempSrcBmp = new Bitmap(srcBmp);
            Bitmap tempMatchingBmp = new Bitmap(matchingBmp);
            double[] srcCpR = null;
            double[] srcCpG = null;
            double[] srcCpB = null;
            double[] matchCpB = null;
            double[] matchCpG = null;
            double[] matchCpR = null;
            //分别计算两幅图像的累计概率分布
            getCumulativeProbabilityRGB(tempSrcBmp, out srcCpR, out srcCpG, out srcCpB);
            getCumulativeProbabilityRGB(tempMatchingBmp, out matchCpR, out matchCpG, out matchCpB);

            double diffAR = , diffBR = , diffAG = , diffBG = , diffAB = , diffBB = ;
            byte kR = , kG = , kB = ;
            //逆映射函数
            byte[] mapPixelR = new byte[];
            byte[] mapPixelG = new byte[];
            byte[] mapPixelB = new byte[];
            //分别计算RGB三个分量的逆映射函数
            //R
            for (int i = ; i < ; i++)
            {
                diffBR = ;
                for (int j = kR; j < ; j++)
                {
                    //找到两个累计分布函数中最相似的位置
                    diffAR = Math.Abs(srcCpR[i] - matchCpR[j]);
                    if (diffAR - diffBR < 1.0E-08)
                    {//当两概率之差小于0.000000001时可近似认为相等
                        diffBR = diffAR;
                        //记录下此时的灰度级
                        kR = (byte)j;
                    }
                    else
                    {
                        kR = (byte)Math.Abs(j - );
                        break;
                    }
                }
                if (kR == )
                {
                    for (int l = i; l < ; l++)
                    {
                        mapPixelR[l] = kR;
                    }
                    break;
                }
                mapPixelR[i] = kR;
            }
            //G
            for (int i = ; i < ; i++)
            {
                diffBG = ;
                for (int j = kG; j < ; j++)
                {
                    diffAG = Math.Abs(srcCpG[i] - matchCpG[j]);
                    if (diffAG - diffBG < 1.0E-08)
                    {
                        diffBG = diffAG;
                        kG = (byte)j;
                    }
                    else
                    {
                        kG = (byte)Math.Abs(j - );
                        break;
                    }
                }
                if (kG == )
                {
                    for (int l = i; l < ; l++)
                    {
                        mapPixelG[l] = kG;
                    }
                    break;
                }
                mapPixelG[i] = kG;
            }
            //B
            for (int i = ; i < ; i++)
            {
                diffBB = ;
                for (int j = kB; j < ; j++)
                {
                    diffAB = Math.Abs(srcCpB[i] - matchCpB[j]);
                    if (diffAB - diffBB < 1.0E-08)
                    {
                        diffBB = diffAB;
                        kB = (byte)j;
                    }
                    else
                    {
                        kB = (byte)Math.Abs(j - );
                        break;
                    }
                }
                if (kB == )
                {
                    for (int l = i; l < ; l++)
                    {
                        mapPixelB[l] = kB;
                    }
                    break;
                }
                mapPixelB[i] = kB;
            }
            //映射变换
            BitmapData bmpData = dstBmp.LockBits(new Rectangle(, , dstBmp.Width, dstBmp.Height), ImageLockMode.ReadWrite, PixelFormat.Format24bppRgb);
            unsafe
            {
                byte* ptr = null;
                for (int i = ; i < dstBmp.Height; i++)
                {
                    ptr = (byte*)bmpData.Scan0 + i * bmpData.Stride;
                    for (int j = ; j < dstBmp.Width; j++)
                    {
                        ptr[j *  + ] = mapPixelR[ptr[j *  + ]];
                        ptr[j *  + ] = mapPixelG[ptr[j *  + ]];
                        ptr[j * ] = mapPixelB[ptr[j * ]];
                    }
                }
            }
            dstBmp.UnlockBits(bmpData);
            return true;
        }

        /// <summary>
        /// 计算各个图像分量的累计概率分布
        /// </summary>
        /// <param name="srcBmp">原始图像</param>
        /// <param name="cpR">R分量累计概率分布</param>
        /// <param name="cpG">G分量累计概率分布</param>
        /// <param name="cpB">B分量累计概率分布</param>
        private static void getCumulativeProbabilityRGB(Bitmap srcBmp, out double[] cpR, out double[] cpG, out double[] cpB)
        {
            if (srcBmp == null)
            {
                cpB = cpG = cpR = null;
                return;
            }
            cpR = new double[];
            cpG = new double[];
            cpB = new double[];
            int[] hR = null;
            int[] hG = null;
            int[] hB = null;
            double[] tempR = new double[];
            double[] tempG = new double[];
            double[] tempB = new double[];
            getHistogramRGB(srcBmp, out hR, out hG, out hB);
            int totalPxl = srcBmp.Width * srcBmp.Height;
            for (int i = ; i < ; i++)
            {
                if (i != )
                {
                    tempR[i] = tempR[i - ] + hR[i];
                    tempG[i] = tempG[i - ] + hG[i];
                    tempB[i] = tempB[i - ] + hB[i];
                }
                else
                {
                    tempR[] = hR[];
                    tempG[] = hG[];
                    tempB[] = hB[];
                }
                cpR[i] = (tempR[i] / totalPxl);
                cpG[i] = (tempG[i] / totalPxl);
                cpB[i] = (tempB[i] / totalPxl);
            }
        }

        /// <summary>
        /// 获取图像三个分量的直方图数据
        /// </summary>
        /// <param name="srcBmp">图像</param>
        /// <param name="hR">R分量直方图数据</param>
        /// <param name="hG">G分量直方图数据</param>
        /// <param name="hB">B分量直方图数据</param>
        public static void getHistogramRGB(Bitmap srcBmp, out int[] hR, out int[] hG, out int[] hB)
        {
            if (srcBmp == null)
            {
                hR = hB = hG = null;
                return;
            }
            hR = new int[];
            hB = new int[];
            hG = new int[];
            BitmapData bmpData = srcBmp.LockBits(new Rectangle(, , srcBmp.Width, srcBmp.Height), ImageLockMode.ReadOnly, PixelFormat.Format24bppRgb);
            unsafe
            {
                byte* ptr = null;
                for (int i = ; i < srcBmp.Height; i++)
                {
                    ptr = (byte*)bmpData.Scan0 + i * bmpData.Stride;
                    for (int j = ; j < srcBmp.Width; j++)
                    {
                        hB[ptr[j * ]]++;
                        hG[ptr[j *  + ]]++;
                        hR[ptr[j *  + ]]++;
                    }
                }
            }
            srcBmp.UnlockBits(bmpData);
            return;
        }