C语言 · 最长公共子序列 · 最长字符序列

算法提高篇有两个此类题目：

算法提高 最长字符序列  

时间限制：1.0s   内存限制：256.0MB

    

　　最长字符序列

问题描述

　　设x(i), y(i), z(i)表示单个字符，则X={x(1)x(2)……x(m)}，Y={y(1)y(2)……y(n)}，Z={z(1)z(2)……z(k)},我们称其为字符序列，其中m,n和k分别是字符序列X，Y，Z的长度，括号()中的数字被称作字符序列的下标。
　　如果存在一个严格递增而且长度大于0的下标序列{i1,i2……ik}，使得对所有的j=1,2,……k，有x(ij)=z(j)，那么我们称Z是X的字符子序列。而且，如果Z既是X的字符子序列又是Y的字符子序列，那么我们称Z为X和Y的公共字符序列。
　　在我们今天的问题中，我们希望计算两个给定字符序列X和Y的最大长度的公共字符序列，这里我们只要求输出这个最大长度公共子序列对应的长度值。
　　举例来说，字符序列X=abcd，Y=acde，那么它们的最大长度为3，相应的公共字符序列为acd。

输入格式

　　输入一行，用空格隔开的两个字符串

输出格式

　　输出这两个字符序列对应的最大长度公共字符序列的长度值

样例输入

aAbB aabb

样例输出

2

数据规模和约定

　　输入字符串长度最长为100，区分大小写。

 

算法提高 最长公共子序列  

时间限制：1.0s   内存限制：256.0MB

    

问题描述

　　给定两个字符串，寻找这两个字串之间的最长公共子序列。

输入格式

　　输入两行，分别包含一个字符串，仅含有小写字母。

输出格式

　　最长公共子序列的长度。

样例输入

abcdgh
aedfhb

样例输出

3

样例说明

　　最长公共子序列为a，d，h。

数据规模和约定

　　字串长度1~1000。

 

 

作者注释：递归超时，递推公式如下：

 /*
 递归思路：
     当数组a和b对应位置字符相同时,则直接求解下一个位置；
                           否则，取两种情况中的较大数值。
 */
 #include<stdio.h>
 #include<string.h>
 char a[],b[];//定义字符串数组
 int lena,lenb,lenz=;
 int maxlong(int i,int j){
     if(i>=lena || j>=lenb) return ;//出口
     if(a[i] == b[j]) return +maxlong(i+,j+);//直接求解下一个位置
     else //取两种情况中的较大数值
         return maxlong(i+,j) > maxlong(i,j+) ? maxlong(i+,j) : maxlong(i,j+);
 }
 int main(){
     scanf("%s%s",&a,&b);//输入字符串
     lena=strlen(a);//获取字符串长度
     lenb=strlen(b);
     printf("%d",maxlong(,));//输出子串长度
     return ;
 }              

动态规划：时间复杂度大大降低。

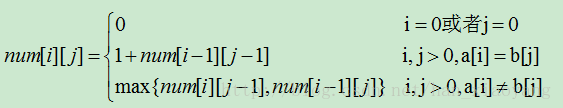
 #include<stdio.h>
 #include<string.h>
 char a[],b[];
 char num[][];//记录中间结果的数组
 //动态规划采用二维数组来标识中间计算结果，避免重复的计算来提高效率
 void LCS(int lena,int lenb){
     for(int i=;i<=lena;i++){
         for(int j=;j<=lenb;j++){
             if(a[i-]==b[j-]){//注意这里的下标是i-1与j-1
                 num[i][j]=num[i-][j-]+;
             }
             else{
                 num[i][j]=num[i][j-] > num[i-][j] ? num[i][j-] : num[i-][j];
             }
         }
     }
 }
 int main(){
     scanf("%s%s",&a,&b);//输入字符串
     int lena = strlen(a);//获取字符串长度
     int lenb = strlen(b);
     memset(num,,sizeof(num));//数组赋初值
     LCS(lena,lenb);
     printf("%d",num[lena][lenb]);
     return ;
 }  

求两字符串的最长子串，有两种情况：一种是不要求在原串中连续(即上述情况)，另一种要求子串在原字符串中是连续的。

下面转载了网上的方法来做另一种情况的。

用矩阵来记录中间结果：例如原串"bab"和"caba"，则数组如下：

　　 b    a     b

c      0    0    0

a      0    1　0

b      1　0    1

a      0    1　0

则矩阵的斜对角线最长的那个就是我们找的最长公共子串——求最长的由1组成的斜对角线：当要在矩阵是填1时让它等于其左上角元素加1，如下：

　  b    a     b

c      0    0    0

a      0    1　0

b      1　0    2

a      0    2　0

这样矩阵中的最大元素就是 最长公共子串的长度。

在构造这个二维矩阵的过程中由于得出矩阵的某一行后其上一行就没用了，所以实际上在程序中可以用一维数组来代替这个矩阵(降低空间复杂度）。

以下代码来自网络：

 1 #include<iostream>
 2 #include<cstring>
 3 #include<vector>
 4 using namespace std;
 5 //str1为横向，str2这纵向
 6 const string LCS(const string& str1,const string& str2){
 7     int xlen=str1.size();       //横向长度
 8     vector<int> tmp(xlen);        //保存矩阵的上一行
 9     vector<int> arr(tmp);     //当前行
10     int ylen=str2.size();       //纵向长度
11     int maxele=0;               //矩阵元素中的最大值
12     int pos=0;                  //矩阵元素最大值出现在第几列
13     for(int i=0;i<ylen;i++){
14         string s=str2.substr(i,1);
15         arr.assign(xlen,0);     //数组清0
16         for(int j=0;j<xlen;j++){
17             if(str1.compare(j,1,s)==0){
18                 if(j==0)
19                     arr[j]=1;
20                 else
21                     arr[j]=tmp[j-1]+1;
22                 if(arr[j]>maxele){
23                     maxele=arr[j];
24                     pos=j;
25                 }
26             }
27         }
28         tmp.assign(arr.begin(),arr.end());
29     }
30     string res=str1.substr(pos-maxele+1,maxele);
31     return res;
32 }
33 int main(){
34     string str1("21232523311324");
35     string str2("312123223445");
36     string lcs=LCS(str1,str2);
37     cout<<lcs<<endl;
38     return 0;
39 }

最长公共子序列应用

有这样的题目：

　　回文串是指正反都相同的字符串，比如abba，他正着看反着看都相同，给你一个字符串，长度小于1000，让你删除最少的字符使得该字符串成为回文串，例子：agddgca，删除字符c就可以组成一个回文串。问最少删除几个字符？

　　想到可以借助最长公共子序列来解决，我们那上面那个例子看一下，我们把这个字符转倒序：acgddga，可以看到他们的最长公共子序列刚好是最长回文串。其实倒过来的字符串和原来的字符串比较，就是那前面的跟后面的字符串比较，如果一样，那么他们就是回文了。

所以求解这道题就比较简单了：

1）先将字符串倒序排列

2）求两个字符串飞串的最长公共子序列

3）用字符串的长度减去最长公共子序列就得到结果