Luogu 3246 序列

Luogu 3246 序列

• 考虑莫队,不算特别优秀,但足以通过此题.
• 用莫队做,先考虑在当前区间右边加入一个数对答案的影响,其他三种情况同理.
• 若加入新数的区间为 \([L,R]\) ,那么加的贡献就是 \([L,R],[L+1,R]\dots [R,R]\) 这些区间最小值之和.
• 用单调栈预处理出每个数 \(a_i\) 左边第一个比它小的数的位置 \(sl\) ,那么它被记作最小值的区间就是 \([sl+1,R],[sl+2,R]\dots[i,R]\) ,被算了 \(i-sl\) 次.那么就这样一个个往前面跳,类似于树的结构.
  
  
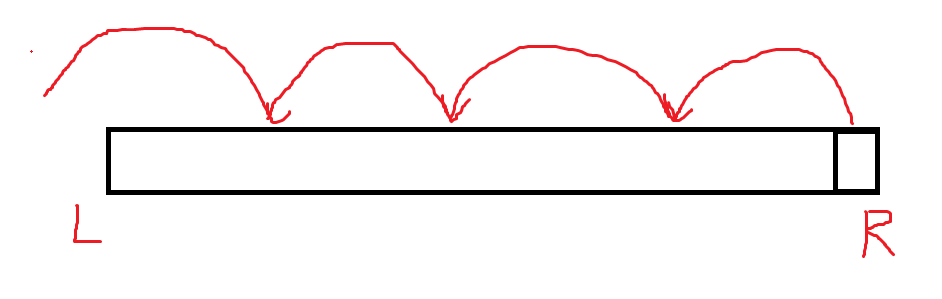
• 这个东西显然可以在算完 \(sl\) 后立刻求出,算一下前缀和,那么每次查询也是 \(O(1)\) 的.
• 注意到最前面那个元素会跳出去,被算的次数不是 \(i-sl\) ,而是 \(i-L+1\),需要单独算.按照定义,它显然是 \([L,R]\) 这个区间内的最小值,用 \(ST\) 表问一下位置,大小就可以了.

写这个题又复习了一遍莫队...询问排序第一关键字是左端点的块,第二关键字是右端点...另外,那四个 \(while\) 移动端点的顺序不能乱写...不然会出现 \(L>R\) 的尴尬情况..如果样例没测出来这题可就爆零了...

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read()
{
	int out=0,fh=1;
	char jp=getchar();
	while ((jp>'9'||jp<'0')&&jp!='-')
		jp=getchar();
	if (jp=='-')
		fh=-1,jp=getchar();
	while (jp>='0'&&jp<='9')
		out=out*10+jp-'0',jp=getchar();
	return out*fh;
}
const int MAXN=1e5+10;
struct query
{
	int l,r,bel,id;
	bool operator < (const query &rhs) const
	{
		if(bel!=rhs.bel)
			return bel<rhs.bel;
		if(r!=rhs.r)
			return r<rhs.r;
		return l<rhs.l;
	}
} q[MAXN];
int a[MAXN];
int st[MAXN][18],stp[MAXN][18];
int n,Q;
int sl[MAXN],sr[MAXN];
int stk[MAXN],stkpos[MAXN],tp;
ll suml[MAXN],sumr[MAXN];
ll res,ans[MAXN];
int mi,pos;
inline void st_init()
{
	for(int i=1;i<=n;++i)
		st[i][0]=a[i],stp[i][0]=i;
	for(int j=1;(1<<j)<=n;++j)
		for(int i=1;i+(1<<j)-1<=n;++i)
		{
			if(st[i][j-1]<st[i+(1<<(j-1))][j-1])
				st[i][j]=st[i][j-1],stp[i][j]=stp[i][j-1];
			else
				st[i][j]=st[i+(1<<(j-1))][j-1],stp[i][j]=stp[i+(1<<(j-1))][j-1];
		}
}
void query(int l,int r)
{
	int k=log(r-l+1)/log(2.0);
	if(st[l][k]<st[r-(1<<k)+1][k])
		mi=st[l][k],pos=stp[l][k];
	else
		mi=st[r-(1<<k)+1][k],pos=stp[r-(1<<k)+1][k];
}
void addl(int L,int R)
{
	query(L,R);
	ll delta=1LL*(R-pos+1)*mi;
	delta+=sumr[L]-sumr[pos];
	res+=delta;
}
void reml(int L,int R)
{
	query(L,R);
	ll delta=1LL*(R-pos+1)*mi;
	delta+=sumr[L]-sumr[pos];
	res-=delta;
}
void addr(int L,int R)
{
	query(L,R);
	ll delta=1LL*(pos-L+1)*mi;
	delta+=suml[R]-suml[pos];
	res+=delta;
}
void remr(int L,int R)
{
	query(L,R);
	ll delta=1LL*(pos-L+1)*mi;
	delta+=suml[R]-suml[pos];
	res-=delta;
}
void init()
{
	st_init();
	stk[++tp]=0;
	stkpos[tp]=0;
	for(int i=1; i<=n; ++i)
	{
		while(tp)
		{
			if(a[i]<=stk[tp])
				--tp;
			else
				break;
		}
		sl[i]=stkpos[tp];
		stk[++tp]=a[i];
		stkpos[tp]=i;
		suml[i]=suml[sl[i]]+1LL*(i-sl[i])*a[i];
	}
	tp=0;
	stk[++tp]=0;
	stkpos[tp]=n+1;
	for(int i=n; i>=1; --i)
	{
		while(tp)
		{
			if(a[i]<=stk[tp])
				--tp;
			else
				break;
		}
		sr[i]=stkpos[tp];
		stk[++tp]=a[i];
		stkpos[tp]=i;
		sumr[i]=sumr[sr[i]]+1LL*(sr[i]-i)*a[i];
	}
}
int main()
{
	n=read(),Q=read();
	int Blocksize=sqrt(Q);
	for(int i=1; i<=n; ++i)
		a[i]=read();
	for(int i=1; i<=Q; ++i)
	{
		q[i].l=read();
		q[i].r=read();
		q[i].bel=q[i].l/Blocksize;
		q[i].id=i;
	}
	sort(q+1,q+1+Q);
	init();
	int L=1,R=0;
	for(int i=1; i<=Q; ++i)
	{
		int l=q[i].l,r=q[i].r;
		while(R<r)
			addr(L,++R);
		while(L<l)
			reml(L++,R);
		while(L>l)
			addl(--L,R);
		while(R>r)
			remr(L,R--);
		ans[q[i].id]=res;
	}
	for(int i=1; i<=Q; ++i)
		printf("%lld\n",ans[i]);
	return 0;
}