MLE vs MAP: the connection between Maximum Likelihood and Maximum A Posteriori Estimation

Reference:MLE vs MAP.

Maximum Likelihood Estimation (MLE) and Maximum A Posteriori (MAP), are both a method for estimating some variable in the setting of probability distributions or graphical models. They are similar, as they compute a single estimate, instead of a full distribution.

MLE, as we, who have already indulge ourselves in Machine Learning, would be familiar with this method. Sometimes, we even use it without knowing it. Take for example, when fitting a Gaussian to our dataset, we immediately take the sample mean and sample variance, and use it as the parameter of our Gaussian. This is MLE, as, if we take the derivative of the Gaussian function with respect to the mean and variance, and maximizing it (i.e. setting the derivative to zero), what we get is functions that are calculating sample mean and sample variance. Another example, most of the optimization in Machine Learning and Deep Learning (neural net, etc), could be interpreted as MLE.

Speaking in more abstract term, let’s say we have a likelihood function P(X|θ)P(X|θ). Then, the MLE for θ , the parameter we want to infer, is:

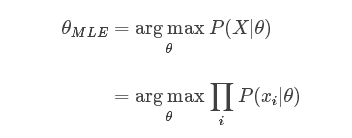
As taking a product of some numbers less than 1 would approaching 0 as the number of those numbers goes to infinity, it would be not practical to compute, because of computation underflow. Hence, we will instead work in the log space, as logarithm is monotonically increasing, so maximizing a function is equal to maximizing the log of that function.

To use this framework, we just need to derive the log likelihood of our model, then maximizing it with regard of θ  using our favorite optimization algorithm like Gradient Descent.

Up to this point, we now understand what does MLE do. From here, we could draw a parallel line with MAP estimation.

MAP usually comes up in Bayesian setting. Because, as the name suggests, it works on a posterior distribution, not only the likelihood.

Recall, with Bayes’ rule, we could get the posterior as a product of likelihood and prior:

We are ignoring the normalizing constant as we are strictly speaking about optimization here, so proportionality is sufficient.

If we replace the likelihood in the MLE formula above with the posterior, we get:

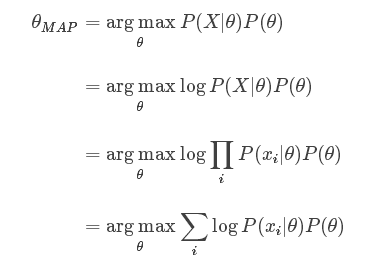
Comparing both MLE and MAP equation, the only thing differs is the inclusion of prior P(θ) in MAP, otherwise they are identical. What it means is that, the likelihood is now weighted with some weight coming from the prior.

Let’s consider what if we use the simplest prior in our MAP estimation, i.e. uniform prior. This means, we assign equal weights everywhere, on all possible values of the θ. The implication is that the likelihood equivalently weighted by some constants. Being constant, we could be ignored from our MAP equation, as it will not contribute to the maximization.

Let’s be more concrete, let’s say we could assign six possible values into θ . Now, our prior P(θ)  is 1/6 everywhere in the distribution. And consequently, we could ignore that constant in our MAP estimation.

We are back at MLE equation again!

If we use different prior, say, a Gaussian, then our prior is not constant anymore, as depending on the region of the distribution, the probability is high or low, never always the same.

What we could conclude then, is that MLE is a special case of MAP, where the prior is uniform!