Is It A Tree? POJ - 1308（并查集判树）

Problem Description

A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.

There is exactly one node, called the root, to which no directed edges point. 
Every node except the root has exactly one edge pointing to it. 
There is a unique sequence of directed edges from the root to each node. 
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.

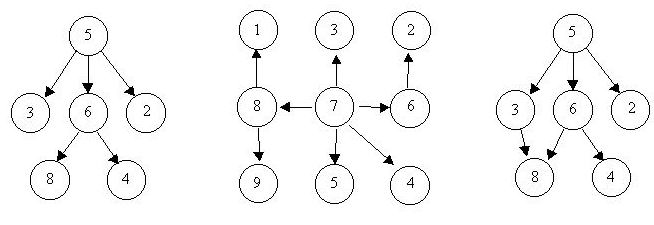
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.

Input

The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.

Output

For each test case display the line "Case k is a tree." or the line "Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).

Sample Input

6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0
-1 -1

Sample Output

Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.

题目大意：

给出多组边，让你判断这是不是一棵树。边的信息以( 始点, 末点)的形式给出以（0，0）结束.，数据以（-1，-1）输入结束；

树的定义：树是指任意两个结点之间有且仅有一条路径的无向图。或者说，只要是没有回路的连通无向图就是树。

树的特性：

⒈必有一个特定的称为根(ROOT)的结点；
2.一棵树如果有n个节点，那么它一定恰好有n-1条边。
3.一棵树中的任意两个节点有且仅有唯一的一条路径连通。
4.在一棵树中加一条边将会构成回路；

思路：应用并查集的知识来判断,将节点以此加入看是否与下面几种情况是否吻合。

不满足条件的情况：

1.要加入的子节点已经有父节点。
2.要加入的父节点的子节点，与父节点有相同的父节点。
3.建树成功，查看树不仅仅只有一颗。

如果1，2不满足了，其实第三步，不需要再进行判断了；

代码：

#include<iostream>
#include<map>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxx=;
int f[maxx];
int getf(int v)
{
    if(f[v]==v)
        return v;
    return f[v]=getf(f[v]);
}
int main()
{
    int a,b,Case=;
    while(cin>>a>>b)
    {
        if(a==-&&b==-)
            break;
        if(a==&&b==)
        {
            printf("Case %d is a tree.\n",++Case);
            continue;
        }
        for(int i=;i<=maxx;i++)
            f[i]=i;
        map<int,int>mp;
        mp[a]=mp[b]=;
        f[b]=a;
        int flag=;
        if(a==b)
            flag=;
        while(scanf("%d%d",&a,&b)&&a&&b)
        {
            mp[a]=mp[b]=;
            int t1=getf(a);
            int t2=getf(b);
            if(t1!=t2&&a!=b)
                f[t2]=t1;
            else
                flag=;
        }
        if(flag)
            printf("Case %d is not a tree.\n",++Case);
        else
        {
            map<int,int>::iterator it;
            for(it=mp.begin();it!=mp.end();it++)
            {
               if(f[it->first]==it->first)
                flag++;
            }
            if(flag==)
                printf("Case %d is a tree.\n",++Case);
            else
                printf("Case %d is not a tree.\n",++Case);
        }
    }
    return ;
}