【csp模拟赛2】黑莲花--数据结构+数论

没有什么能够阻挡，你对被阿的向往。天天 AK 的生涯，你的心了无牵挂。 虐过大佬的比赛，也曾装弱装逼。当你低头的瞬间，才发现旁边的人。 把你的四肢抬起来，使劲地往门上撞。盛开着永不凋零，黑莲花。 ——cx & cyx《黑莲花》

　　这是一道数论题。

　　

T3

请此题爆零的同学写一份心得体会，明天交给我。

对于区间修改，将原数组差分之后使用树状数组即可。

首先要知道扩展欧拉定理：对于任意的正整数a和p，且b≥φ(p)，有：

扩展欧拉定理的一个重要应用就是降幂。

而对于询问区间[l,r] mod p（其询问结果记作s(l,r,p)），可以推出：

（假设上式中出现的模p意义下的幂指数都大于等于φ(p)）

将p不断地变成φ(p)需要O(log p)次之后p变成1。

而指数为1可以直接计算。

所以询问s(l,r,p)可以递归做：

（1）如果l=r或者p=1则直接反回a[l]。

（2）否则递归到s(l+1,r,φ(p))，记其为t。如果t≥φ(p)则返回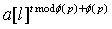

，否则反回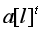

。

剩下一个问题：如何判断指数是否大于等于φ(p)。

注意到。

所以，我们只需要取出[l+1,r]的前5个数（如果[l+1,r]的区间长度不足5则取区间[l+1,r]内所有数，如果[l+1,r]内第一个1出现的位置为x则取[l+1,x-1]内所有数）

如果取出的数的个数为5则一定大于φ(p)。否则可以大力快速幂判断指数是否大于等于φ(p)。

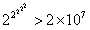
可以用线性的欧拉筛预处理欧拉函数。

复杂度。

实测：开O2优化并且使用普通读入优化：5.8s；使用fread：3.4s。

良心搬题人为了防止卡常，开到了9s。

这是一道数据结构与数论结合的好题。

代码：

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cmath>
#define int long long
const int N = 20001000;
using namespace std;
inline int read()
{
	int x = 0 , f = 1;	char ch = getchar();
	while(ch < '0' || ch > '9')	{if(ch == '-')	f = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
	return x * f;
}
int phi[N],ans,a[N],cnt,prime[N];
int n,m,opt,l,r,p;
bool vis[N],flag;
void yilin()
{
	phi[1]=1;
	vis[1] = 1;
	for(int i=2;i<=20000000;i++)
	{
		if(!vis[i])prime[++cnt]=i , phi[i] = i - 1;
		for(int j=1;j<=cnt && i * prime[j] <= 20000000;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				phi[i*prime[j]]=phi[i] * prime[j];
				break;
			}
			phi[i*prime[j]]=phi[i] * (prime[j]-1);
		}
	}
}
//////////////////////用线段树处理区间加，单点查询
int tr[N<<1],lazy[N<<1];
void build(int k,int l,int r)
{
	if(l==r)
	{
		tr[k]=a[l];
		return;
	}
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
}
void pushdown(int k,int l,int r)
{
	tr[k<<1] = tr[k<<1]+lazy[k];
	tr[k<<1|1] = tr[k<<1|1]+lazy[k];
	lazy[k<<1] = lazy[k];
	lazy[k<<1|1] = lazy[k];
	lazy[k] = 0;
}
void change(int k,int l,int r,int x,int y,int val)
{
	if(x<=l && y>=r)
	{
		lazy[k]+=val;
		tr[k]+=(r-l+1)*val;
		return ;
	}
	if(lazy[k]) pushdown(k,l,r);
	int mid=(l+r) >> 1;
	if(x<=mid)change(k<<1,l,mid,x,y,val);
	if(y>mid)change(k<<1|1,mid+1,r,x,y,val);
}
int ask(int k,int l,int r,int x,int y)
{
	if(l>=x&&r<=y){return tr[k];}
	if(lazy[k]) pushdown(k,l,r);
	int mid=(l+r) >> 1;
	if(x<=mid) return ask(k<<1,l,mid,x,y);
	if(y>mid) return ask(k<<1|1,mid+1,r,x,y);
}
/////////////////////////
     c
   b
 a
int ksm(int x,int y,int p)////快速幂
{
	int res=1;
	if(x >= p) flag=1,x%=p;相当于b 如果b 比p大，那么b的某一次方一定也比p大，这样才符合公式
	for(;y;y>>=1)
	{
		if(y&1)res=res*x;
		if(res >= p) flag = true, res %= p;////快速幂，如果当前处理的值比p大，记录一下，之后才能取模，如果直接模，一直会比p小
		x=(x * x);
		if(x >= p) flag = true, x %= p;
	}
	return res;////不及取模，影响后面对于和p 的判断
}
int solve (int l,int r,int p)
{
//	printf("%lld\n",ask(1,1,n,l,l));
	if(l == r) return ask(1,1,n,l,l);
	if(p == 1) return ask(1,1,n,l,l);
	int t=solve(l+1,r,phi[p]);
	if(t > phi[p] || flag) t = t % phi[p] +phi[p] , flag=false;
	int ans = ksm( ask(1,1,n,l,l) , t , p);
	return ans;
}
signed main()
{
	#ifdef yilnr
	#else
	freopen("zzq.in","r",stdin);
	freopen("zzq.out","w",stdout);
	#endif
	n=read(); m=read();
	for(int i=1;i<=n;i++)a[i]=read();
	build(1,1,n);
	yilin();////线性筛欧拉函数
	for(int i=1;i<=m;i++)
	{
		opt=read();l=read();r=read();p=read();
		if(opt==1)
		{
			change(1,1,n,l,r,p);
		}
		if(opt==2)
		{
			flag=false;////对于每次操作，要先把flag 赋值为0 ，因为此次操作与之前无关，需重新判断；
			printf("%lld\n",solve(l,r,p)%p );
		}
	}
	fclose(stdin);fclose(stdout);
	return 0;
}