周志华-机器学习西瓜书-第三章习题3.5 LDA

本文为周志华机器学习西瓜书第三章课后习题3.5答案，编程实现线性判别分析LDA，数据集为书本第89页的数据

首先介绍LDA算法流程：

---

LDA的一个手工计算数学实例：

---

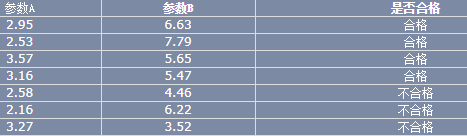
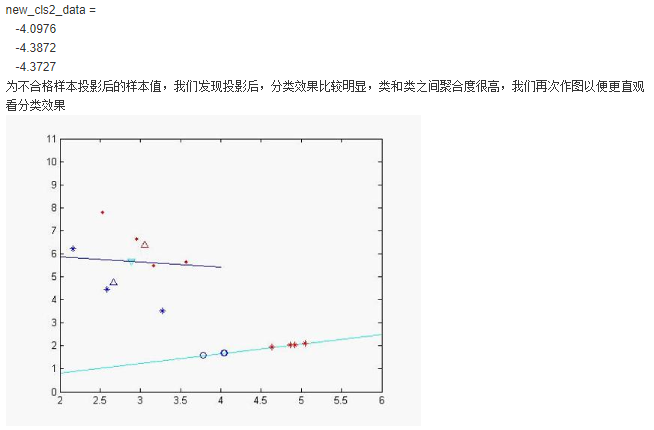
课后习题的代码：

# coding=utf-8
# import flatten
import tensorflow as tf
from numpy import *
import  numpy as np
import matplotlib.pyplot as plt
def LDA(c1,c2):
        m1=mean(c1,axis=0)
        m2=mean(c2,axis=0)
        c=vstack((c1,c2))
        m=mean(c,axis=0)
        n1=c1.shape[0]
        n2=c2.shape[0]
        s1=0
        s2=0
        for i in range(n1):
            s1+=(c1[i,:]-m1).T*(c1[i,:]-m1)
        for i in range(n2):
            s2+= (c2[i, :] - m2).T * (c2[i, :] - m2)
        sw=(n1*s1+n2*s2)/(n1+n2)
        sb=((n1*(m-m1).T*(m-m1))+(n2*(m-m2)).T*(m-m2))/(n1+n2)
        a,b=np.linalg.eig(mat(sw).I*sb)
        index=np.argsort(-a)
        maxIndex=index[:1]
        w=b[:,maxIndex]
        return w
data = array([[0.697,0.460,1],
        [0.774,0.376,1],
        [0.634,0.264,1],
        [0.608,0.318,1],
        [0.556,0.215,1],
        [0.403,0.237,1],
        [0.481,0.149,1],
        [0.437,0.211,1],
        [0.666,0.091,0],
        [0.243,0.267,0],
        [0.245,0.057,0],
        [0.343,0.099,0],
        [0.639,0.161,0],
        [0.657,0.198,0],
        [0.360,0.370,0],
        [0.593,0.042,0],
        [0.719,0.103,0]])
x_train1=data[0:8,0:2]
a1=x_train1[:,0]
b1=x_train1[:,1]
print(a1)
x_train2=data[8:,0:2]
a2=x_train2[:,0]
b2=x_train2[:,1]
#样本投影前
plt.scatter(a1,b1,label=' + ', color='g', s=25, marker='o')
plt.scatter(a2,b2,label=' - ', color='r', s=25, marker='o')
W=LDA(x_train1,x_train2)
print("w=",W)
k=W[1,0]/W[0,0]
plt.plot([0,1.5],[0,1.5*k])
# print(k)
# new1=(a1*W[0,0])
# new2=(b1*W[0,0])
# new3=(a2*W[1,0])
# new4=(b2*W[1,0])
new1=a1
new2=k*new1
plt.plot(new1,new2,'*r')
new3=a2
new4=k*new3
plt.plot(new3,new4,'*g')
plt.legend()#设置图例
plt.show()

运行结果：