RNN汇总
RNN(Recurrent Neural Network)循环神经网络。
对于CNN来说,比如图像处理,它逐渐从局部空间抽象到全局空间,有一种空间层次感,通道可以与空间一起卷积,也可以分开卷积。同时由于卷积权重共享,它可以减少参数。
对RNN来说,它擅长处理序列问题,也就是输入中存在依赖的情况,比如预测下一个词语(N对N),情感分类(N对1),encoder-decoder(如seq2seq,N对M)等。
本文力求简洁,仅做概要总结。
1,简单RNN分析
aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD//gA8Q1JFQVRPUjogZ2QtanBlZyB2MS4wICh1c2luZyBJSkcgSlBFRyB2NjIpLCBxdWFsaXR5ID0gMTAwCv/bAEMAAwICAwICAwMDAwQDAwQFCAUFBAQFCgcHBggMCgwMCwoLCw0OEhANDhEOCwsQFhARExQVFRUMDxcYFhQYEhQVFP/bAEMBAwQEBQQFCQUFCRQNCw0UFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFP/AABEIAdQCWAMBIgACEQEDEQH/xAAeAAEAAgIDAQEBAAAAAAAAAAAACAkGBwEEBQIDCv/EAGsQAAAFAgMCBgYOEw0HAwMFAAACAwQFBgcBCBIiMgkRExRCUiEjYnKCkhUYMTM3OENXdneisrTCFhckNDU2OUFRU3F0dZSVlrPS00RWYWNzgYORk8PU4/AlRVRYo7HEoeLyGSYnKWbR4fH/xAAbAQEAAgMBAQAAAAAAAAAAAAAAAwQBAgUGB//EACsRAQACAgECBgICAwEBAQAAAAACAwESBBEyExQhIjEzBUIjUkFRYnJDcf/aAAwDAQACEQMRAD8AtTAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHHGGOIi3fDPbSVsqkWoykot9cy4ZccSGg4LzpobsfPS/ZKl7oxelgUaRlLh5prnGMs9rSnrTRyu7HQEeWQdkL3Squzq7w43jVKfa21ysQDsCtf5V11jm5RXMdX/OOuiuUiXiD042czP24OReEuxE3BbpY/QyrYciWruecJbXuxL5exnWSxgBDy1nCFxK9QNaSvDTTq01UuTaGzt2rysQ9N/FOt0vhbPdiXxFCqEKYptRTbpiivn0+Wj9QAAAAAAAAAAAAAAABxh2Bxj5oizfvPNA25qZehqEg3NzLjlxwKrExiulqw++nG6l3vjaRoSWTzDXfOdzWt21aGjlf9w0Alzfki9XnRu26/HEsapT+G0YrIuPH7A448fsCsFTKNTj03KydXV1MO94zh7UKpldQ7bOwtVUSbl6AvbX1MLk3G76Q5+y/sDbJxN5Sxt4clmnFgORX/AE3nNu1YdRNK9FON61pAuyas6STxK4al6zpr8YujwhNS3lw6butSzKpKVmm07DvCa0XTQ+on1uMpuqbDsbJtovGK0oSh3I2WAADUAAAAAAAAAAAHmTE0yp+LdScm9QjmDVMyy7t2qVJJIhd4xzG7BS/wiGlbcIPI1pJu4SwdEq1zigYyS1VzBjNYdE3cdNf3HhBGOZ/Am2ArlfkzJV3idapb4lpgp/8AdlIw6SRCd44N20dIlsbux5uUY5j66I4674xXSXiGFny1jfWSyfzfrDnSK9Yu9uaK0Z+UeuabvVCJeepHQ8iJMxe5MXtXvxIrL7nJoTMG7UhW+LumK3al+bKUnic3epcXFqxJh5ipe97PWKUQyrnDua6pBAADRgAAAAAAAAAAABjtaVtBW6ph/UNSybeHhmKfKOHro2khC/66IDIMOLEdd68Qj25l3K6aCJN5RU2kuH9YgHVOby7WYtws2s5HpW7oUx9Ba1qBtyr16XrtWptgpO7P4xDbIwZfKbT1WuivrjVLVFypXeMrPSqvIkN3BSnLpL3IsxolJtGEliJLs0OdfkCVhAHcfaiyiGr+rWMnQcJO0iqoqFVSNunIbUUwrWNlAs8ZLksKFYYE/lVdfj6x57PKwxodXF5bGtKptk/KfWXyKklVWhzfxqCptrxxvLiSb+HJaAOOMQGovOtcOxDxpFX6jEZ2mFTlSSuDTjfjwR8z59bl3e+J4puMTjp6oYurYVlMQ8g2lYl6kVdq9aKFVSWIbdMQxfNwFWUMw7kT1wABqAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADjDsCD2a3MVUlfV+5sfaaRNGO26eurquRx+hSRv3Khxern+z0fGMTfebK9/lfLC1RWLfAi0wijg1im+PEblXipuTS2elpMbWbDqkMIpWGtme2FAtm0iqZ5UsmY0jOSCptSrl4rtq6jdLRuizRV4km8Y7PXtlammrSQBYinY8rYuO2u4NtOHR+sqbpGGXgOktNx7aRbx6sg2JIOPOmh1y8qr3hN4drGIQWndADn0F1GHQhKhjKkZ88h5NpKtNRkuWYrlVJqL0NZRt1HUrCjYOv6ecQ1QRiErGLl2m7gvuydQ3dkGJWGvLO5Q67hrb11KuJm0c04wa03ULw+tWEXNutHBvtWPRN0e91aNjjGrl0DGXQomVpiXS1sn6enX00j9BUvdENtCrdT4keqOUdk8wEWsgF4ZW41nnVM1Sryta0K/PTsqY5ttcqfzu48Mmzq6ZkzmEpRxOnRWAAAAAAAAAAcYdgQxzh5i6heVk3sbax7zKrXzfnFQz6WPYgmBup/HnLu9XUTr6iSXvLcljZ+1VV1pI8R2sJHqveSxNp5UxS7CXhH0l8IQKyzUnINKNdVrUpsHNa1suaclXZt/tu0kl3pSG3OhrOLFFXiybxjszC2FqqftDTpYin2mjXtunau04eK/bVTdIwy8fk8eNo1uddyuk2bk3llTaCFGK0/d+iqsqVWn4Op4uYl0kjODN2K5VdJC7+2XZ6Y7eNYe1aZeA6FQ1DG0tCPZeXdpsY1mlyq7hU2wUg6tHVpCV/AoTVPSSMnFrYnwKuhhxY4Y9TuBnYeychTlOUxdZDDR6+E5k2rRxcy3bZRzQ7pUhqtotLzk6XTdNS9BUn+tgbwHysik5SOkqUqySpdByHLrIco0srjbFiUdksaJrKIuJSkVUkC8TkIWTblctXSfmHKYe+IIZCqkWtVdOvbEO3CmMO3L8k1KlVN2CM1T6XCBe5Iqb35hO7HHsDgTjpLVTcgADUAAAAebLSzOBjHclIuU2cezSMuu5XPpIkmUuoxzG6uGGA9EQm4QquH9XSVE2Hg3KjZWr1TP6hctzbSMSgbaL2Ptpy4l8DT0wjHfPQajrStJjPlVKr16o7h7CxbrRGQ5DGRWqNUhvnhx0uS1bpPjDb0VFMYGNbx0ezQYMkC6Em7dLQRIncECHh2cDFNIyPbJM49mkVug3SLsJFLskIP1ePEGCB13K6TZIm8qsbQQg71VUaorkY6v1Addg/bSrNJ4xcpPGipdaThubWQ5e4OOu8qGKYSjSMcybRtJutZ0Giy5SKq94TeMJ2XoDXl17LQ10UW7zlFoWqo43KxVRMDck6aKF3DFMTeJ3A2GAxKEZj3cneaGZr2SkrV3OKkyulT5MFcHCWyjNs+g6S7rrk/n65SSwFZeY+DlINjD3VpTtFaUIv5KNjl9Xal+eED9Yhi6/d9cWEWzruOuhQNPVfEGMpGzbFJ+hx7xSqEwNpN3Rd3+YcG+vwpaqso6stAAELQAAAAAAHnv5FtEsXDx4um2aIJmVWWVNpImUu8YxhWtUFTPc9Fxj1VM4Lo2Yp94ZKm4E+ohZlcmyZ64L0i9Qng9fXvXhH67kErfUtaqBXO2mrkSvkWqql2DJR6ek7s/i4kL3pjjxaep5jSsDHwsYgVtHsECt0EidApSC5xqtpbSTVxd5FEqKREkilIQpdBCE6I+hh9f3foy1iZDVVULSKOcvKlRNrOscvXIQu0Orae89LXqi5CQpZ4o8bs3PNVOVSMkfVo169JuiOxtDtTs6Aa+u9falLHtopaqXK6JZFc6SBG6HKn2N8/el1EGcsH6EqwbvmapXLRdIiqSxNw5DbZDhtEfb9g2kmThm8QSctHBTJKorF1kMXqHINTWrrl1kbuaxjV3KytiaqeYIHSWNr+Rt+pjsHKb7Qbpf8As29vDH7hUNH3IoqYpqVS1spJAzc2zum6Byd0Q2g/gCC+rxYsSjsnYQ5Tl1Fx7ACLvB63Wk6+sEnA1Cry1VUO+VpiSMbeNyHYSP8A2WJC6+kYhwHC+PRTSkAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHGPmDkcY+YAg3whD89S3ay90Djjidm7mnc86Swx7BuZpFMnq8c49cY/nXSMzzh5fnimHEi6j5tqkb+MKkU3xsBkA6nE+FmvtdKYh209FuI94VU7RwXQqRJU6R9PflOQwgbfu3cRYPNDbGaphNWOYyLxudZAy51dsjgpVcdZjatohyif4hRwkiJmOFtpou+1dui6/7I5feCxyI+3YkmVPQ6FQwchFOjGI3foKtVTom0H0mJoPoEdcmtrT2zkblNWMspLU+SURYs3WJdGCqqRDctjo7k5uT1/ZSG0rnVhIHQj6VpdfRVdQl7Q43+YNfVXp+817PWMcgy6j6Sj6GpeMgYpLkY9glySWvfP1zn6xjn2zjOI7S6pHrgPlFym5KcySpViFNoNoNr2h9CwMNy0PsaLz8VhCp46GVZUehLnL0TOmy/JF9xrE/vsCvi1CZpDhF6aKh5rChHi6+BeiQ7jQX3RxYP8AYHn7vskqS7nOHmDkcYeYORE1AAAAAABDrhRJBVfL5AUqicxS1hV8XBK4E6RDGOt75Ao6iKJWyREkilIQhdBSE6A/XhPETNraWsm+L5nh7ixDtyfqJaXBdXjGKPgdLifsmrefN09FVIy5nMRjSVaa9fN3yBVSau8MIRy9MRtpOEFpVKDZoxcZKpEW5o2JpSJyqSqRtJe+JqE7BCfNwXyDzb2bmt3AyrVIxsPsEe9n9KLV3bs3kltcWmYOsqGm4Wo9iCdNjc8Pyunkik29ero6NGvwBq3JxQRKGtIsZudx5Gy8m4kmJHWHErzU2gjcxu6MQhDeEPdrw5rtVUegGZjfI+zMVxUzsnSLvpR5D9Y+8bue/Gz1lm0UyOqoZJm0bpazHObQRIpfelGce7OyR2AGG0teig61lzxUDV0TKSRf3O3eFMc/edbwBmQn2GrZt58hmcXL9UqGOKZn757TzrHD1RJdLtRfGPqFjorauKkaWzL5cIhPbcGqg0hp7hBLWcWSjh8j7FWXy+sPMHI4w8wciu0AAAHz9YVyuHpq6zy3wqBfbRp5COptjj1S8lyqpf7UnuxY19YVtW+RxYZnMyMet88FqZJ3jr+1KpayCzxvsbx7m2RovM/Yam68t3Vs24aLmqBrHKvWrnB4roKZJLUUnJa9OnZ6g3oPPqSN8mKclWP/ABTVVLxiaR15x2gtI8cHzUKs3l8SaqqmP5FyjhqXV0C7Cv8AejoZpLKpVPd22tURsss3qVWTasEo8pNWJkkjmcHcE6vJE1mN4IxXg46lbRlrq7LIOk2jSOkCPV1lj6SJEMltGN/ZCQNsYpzWdRu7kTSCjY7xDmsAxcE22TDf5U5Oiq42Dn6pdBRBH3QjFH+rZ4DpSU3Hw/I8+fNmfKm0F5wqQmo3hDu75dRRcSPyeNkn7VVsuUqzdUp0lSH6RTD0uDAlFsMuspSblTFZSi6plIAuJ97SVXBX+/MOkPz4MlMytL3pkSYcbR7cmVOhj1i6Udoc7mfqgsTSAAHLQgAAAOMfMHI4x8wBAHMm5NUnCE0vHqbbam6DVkEy9VVd0dI/uNAzEYXmEQxp/hEYd2pjoQn7fmaI90qk8Mc/uCjNB2OJ9azX2vyeM0H7VVs5QSct1S6FUlS6yGL1BCnIGj8jF0ruUqXHSk1ckIQn8k4VS+OUTbEH7CyLSic694U5FdJowMg/eqrKm0EIXnCSurxDnG9ndGRJvLNlSlP1tbxvCP41OUqOSdEZU8TUciqTpX1XZ6JC6jm6Gkg25TEClStMxUKgYx0o5mk1Kc/TKkTT8QYDbeNc1zUZ7jTTZRsRVAzWno9wXbasj76pydFVxsH7kugnXG0BLHu2SADFY25tOzFwJKimj7nM/HNiunjcpNhIpusfrbZNgZUJNhj+Sd0ans3N+afS1YM5RlEzRS/WKroMRU3hHP8A9gHxkwanms5d9JlPDU1jImJisT/ZMcnK/ExAebu78qsvlPEAAGgAAAAAAAAAAAAAAAAAAAAAAAAAAAAACGnCX006Z20o650eidZ1b+oUJJ0Qu8diqbk3BMPu48l4OodSNftpVg3fM1SuWjpIqqSpNw5DbRDiXlU01G1tTMtT0y2K9ipRsqyeNzbqiShMSnLj4JhXDbosrl2uI+sVWa2JsG2pekJhfclI7VsJavtqW7o/U273Ft0lrlNXLo3UIr8IXST2rLd0k2jWyjuSVn026DdLDjOqdVFX9QZxK5vqEh7jzFGOcJDyRjinLyyLXlSOl/tCRC7RlNvqDLqJpiVqGcJWlXNebSfJHJEw2rWSIQNv6usufpH6O6Tp6+jLW2OsU3eWct0+o+I8k6jclkqwkUkiSLsm4kUpNBG6X8UT3RtZumMlrin21TUxIR7ld2i3MmbUdk5VQPun6RTlMPdHVlfoU7/kDe8GdekdWWiMiJzKZb4I5jajc5ebR/5cwkCI+5EPS2QX3y8+EGGSXwriZfvI21lBFxf3Gqz5lbETN9Dmp/PXSvUKUmv/AEQRYnpXsx+rYGQaI+WJe+8l2tGB4oiyVIwq/XSQ4jODF7k5+SMJ14+YNfWKs/EWFtPTtCQm2ziW3JmcGw4jLqmx1Kqm7o5zGN/ONhDjTlvLZTAABqAAAAAAA0fnMtGve/LTXVKMEsVZVVlzyOKTfO6QOVdIhe/MTR4YjLYy4id0rV0/UBTcbtdqRJ4T7U6Lsql8YosIxxFcN8KPXya3wkKnTQN8pivXnLvFEibMFLG3jn6qSv8Arc2rfGs0l6t4y6NpCJucW2czdK61rYymVUyS6eLpwoufb5mgQ6RucHJ1dXH3x9ke3RWctW49WVLTlOULIv5NqryUYYival9oxTquDae0F6fSG6re0MalUnchKvPJWqJQxVZGT06NR+gkkTopE6BPC3jGHUlrbHWKz3u9Q1EsaApxKKYmUW2jKunbg2tV0ubaVVVN0zHMOtcKg2dyItpESpjHhOdFcPmJP3YUuvQkbudeg3gDKB15KSbQ7Bw+fOUmbJuUyqrhU2ghSl6ZxLrHEGUVs3FlqapqkafnKKhGdO1gjMs2sYaHblQM4OY3YLoJvY9LwRK9HVyROV39O0Ncw8IrX9UMqznEDNoyOKfyCj3BdByat96qToqnJuE6Je7Pseddy8LiOZQ9N0AQtSXBqz5ngWTTb2T/ALqP1Uik29W7sdTWIM5jD3MdrIctsKa8GdmZqpLDloC2kQaKQcdA0o589096lrIYWCeZxjT+VuwLDLnZ6MpVFbB9LGOd/MSXFxGePlfPVf8AsQvckKNw4+ZiOLOW8tlOTkAAaAAAA+fNxFfF+4c1pc+CUooXkoS50EREq26XyRZ7On+y0eOLCBoXOHl8PmGtCpGxS2DCsodcsvTshgbRyD1LskLifi3T7vim6I3hLSWxHLVgCPKWcSn6atcrMVcxdsKrjHhYiYpxJPicIPNvXsn3C7BzavAGQNbjKX+aN46hlnjKml0iHlqjxIdI6RDk2mrf+P6Jj7iXfDtYsjPHRb2R6yg2RnJmZrLyVx5vQB5fiO00/RRVqqroJ/IEMbUbrGIQvWE6x0oSEY03EtIyMbJs49qkVJBuiXYIUo7okrr1izGOrUFd5dKCrEk3L1uieXdOCqnNJunR0uYIE3CpbehIpC+NvGHVyfQ1QwFkI1vUKixuNdU8cR156Rnr7Vq9/wB6cgzq5trKfu5AKw1RpuVmRi7rd4q30H6+yfSbw9Q1RlGbzdLq3BoaSfLS0TTEuRpGOnBtRuSMTVyXgl07HdiHssP2beujXLa2lvKgqh4YvIxzMypSH6SvQJ4Z9BBuvINa91anKvRTCSJiWalEjzchrw28VXJuV2u6KQyZfAEWafprHObfdlSDInObUUS8I/qWQJ51JPS+dMidcvX8PuNVlpS4EwwLh5gocmzeStZLq/QBwORTaAAAAAAAhdwkFKOoSCoC8sa3Mu6t/Ma5AiRdo8Y50pOMPeeOYflGyTaYjWj5muVy0dJFVQVJuGKbaIcS/qKnY6q6fkoSWZpP4qSQO1dNFS8ZFUjl0nKbwcRVjXs3U+Q5xO2/l45xPwR0lXVAyquGOBHJdXzkqYvqqWvwvDILnGv09sksJaJLiJFM5f2108zdZ1+5WwVolN0mggkj51KrlSS5Uh+ukRUu10TGL3wy621WXMv5RzNnUUAvQMebV5KyJMDN3D0mrYSapG2kimJvqm8Dud/xUUzhI1pHx7ZNmxapESQbol0ESKXcIQdLH8qfvdoYfcWrXkC1aRUGUrmqJkxm8ckfcS67hX+KSLtG6+wXpjMBo2r7V3Vc3NmKopatYWNbvEEmrdKQjOXVbpFJulN3Z9R//iNrP+WWEWXpNtROcOuolsqq5wSpxssu7cbarpU5kTKqm7s5jGMJKVZU0fRVNSU9KKckwjkDLrmw6pRDyh6eugjm4qdBWsIfydQh2ysm+8j+0rttaXaiE6JvM2hu2n6ac55bqJUnD4qYWbpp4RxUs4l51LOC7RGDc3TL1jeF1NdbxPDii31ikLwcNv5KnrIva4n2+LeoLiSqtSLlPvJoK/O5O80bZf5UBKho0RYNUmzZMqKCRCkTSSLpKUpfMKUByM+qu7gAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAANQZicudL5lKIPA1AmqwftFedRU2yx0u4xz0VUje+J0ux9fSbDb4AKqpJvO5T6vUWvPRbRyRY3INrrwkWVQjwu6TnWkutJX33db43hS1ZQNaxxH1PzLKXam9VZLkV0eLuCa75g2lWazR23TctViaFEVSaiGL1TFEYrn8HnYKcUe1GeBUoR2gmZdaTph6eNKkUu0Y+gvai+ILlXJlBNGxjg8CuXiTCmXZ155lTaRynIaQfaNCRfCOQojhkytrSWbOo7gQiF37qQmMG+MtFNU6hLrdxZj4lSVNqS3ym3/5UgmVSvBnWUhZJKQn4+br6QT3HFWSyrr+shNBDeEUTS5n/ACeIhlY19UxYw9r8v6S1xubqKYHqSQZc3jIgyptRjnX9V6Wzp73Xuie+V3KbFZeWUhMyL9WrrjTmOB5qpnRNtX+KSL6kkXq9LTh3JS7wpynIqk4ZtFQkW0ho1qTSgyYIFQRSL3JC7I9gUJWSkj2cYDkAGjUAAAAAAAAAAHh1hSENX1OP6fqCOby0LIJGQcsnRdRFSfYxHuAArmqrLTc/KS7dubbMHN0LVmPyvyN6v9sRP3v/AMQXud7uekOtROZ23VbKc2LUCMJLkNoVip75idpH6mlXeN3moWQ/W7I1xczL7be8Sf8A97URCVEvgTQV27ZkxcEw7lXfL/MYWKuRKDeMtEdGzlJ4kRVBVNZI+4chtZBqu/8AF28qymyxteVcSCiklMVVW6UqRry5ujqJvG70aCtDSeWu7Od+qLefIriyoR7rYU4q0l3RSqu0N8+vleyRfiV0dnopcW9iLGaK4PrL7QDsrmNtjFvHBN08sdWQw8Vc5y/+gnly9v1b+IrHjcuEJmBeLwdjKYqqpinNyS9VzT9VrCM+vtGJqVN3HvxZdlTybQWWtopMSD09WXAfokRf1G7T7KaRS9hu3L6kkXQXvtOHmbJSyIYMW0a0RbM0E2zZImhNJIugpS9yXAd0U5TzJCAADQAAAAAAAAAAQ6zi5E46+UknXdIYR8bcZlhhyiUi2KrHTRC7qTtPr/WKr/7cS6Ipi/kfQb9vQ1zacNaOp2peSKxep8lGLl67VcnatH+tZxZ35uAxeu7cUxc2DNDVVT8dUcUbs4tJNqRwTV2dourdN3QlrtlV2t4y1RVZvEH7Ujlsum5bql1lWRNrIYfqNWZz8pNl8tNmqguBTTyp6FliaW0YzgJ5VJJ08V7BCaVdeOji1nNoMXYIYMsuT6kcytmKardW8l1XST9DAj+M+SImBEHRNhZLzrd1YbPc6Rc83/y38Ri1V4vLSOpGQqK+qkZCuVDqpspBi1VdplN0UDbxvEN5m4PztJauusyUThBUDHyduLSuljLylbTJP9qzhj8XKnblNt7f23d73ToExLW5BrIWnfpybCim8xNlx1YylQKHkVsT9fDleMhTd0QpRIfAuBOxgK075S7WmzCbRWjpix9BxlIUhHFjYZiXYLjhqOofpKKG6RzcXZNiM5ABXaAAAAAAAAAAAwO7dn6UvnRL2k6ziSS8O5w3D4aTpn6KiZ94hy8e8M8ABXFUtl73ZWjGSh2Dq9ltUuwhyGOHk9HpdUxPV8C9z7geTT2bm2E2udo+nvkYlUjaF4+oUDslUD9Q2rZ92LMeLsjQucCZt9QFlKjrau6UgaoJFtTc0bTMek4wXcm2Eki6y9I5i4djo6hZhyZQbxlLCPR72W7Ilypq9pnkuv5MN/1xhk1m4t00eFjYOQd1rOq7CEVTLMz1Vc3cadn3QxngtoSzl+qYqGmqzt3SsrXEIsZ6m4dRiRjOmap+ru9qUNo706Qs0pK3NLUA1M2penImnEMd5KKYpNSG+7gQuAlly5N/EV5Ubk2uJmVrN3VldRZ7O0nIoEbvI9oviedmW5dGlJwfdbk2CbOnV3Jt8WDW+t3T9raUjqapWIbQkIxS5JFq2JsYd1j2do2PHjqMbaN5oy0ccQpynmfyhcgADUAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAECuFtzG42wssjb6Jd8lPVngdJxoNtpRxfPf7U2lLvcVROaSkm0NHOnzxZNs0bJmXXWUNpKmQpdRjG/wC4/nUzf37d5kb9VJWZzq4RZ1eZxLc/qLJLjKl420c3dHMA6GVW+r7LhfWma4b4KHaNFuRkW5MPP2auysT7unaL3RSj+jaEnGFRQzGVjnKbuPfoEctXKRuMqqRy6iGL90uI/lr04/YF0XBEZjflg2keWzmHOB52kMMDseVNtLRxzbP9kfY70yQCwUAAAAAAAAAAAAAAAAAAAARK4SbMaXL7l2kW0c45Kqqp1xEZoNxHSIYvb1/AJ2O+OQS1FIXCGJXazGZh5dxGW3rRxScBqiYjRAOzJKkIbtrgvavVDajaurgQBCmnZ+RpidjJqKcnaSUa4TdNXCe8kqQ2ohv5jcQ/o5yw3wj8w1kaZrljoTVkENL5sX9zui7KyXj7vc4lH88cfaat5Sp3tOsaPn3tRsS8s6iG8Yud2gTZ2jpFJqKXbJ9bplFjfBNy9y7R1zM2+qyhKqiKVny88bPJCFdJN2r5MnSOYmBScqkTT3yRMAFrYAAAAAAAAAAAAAAAAAA0jnAv42y32EqSsjnJjKkS5nEon9Weq8ZUvF2jm7khgFXXC15jS3SvUjQMQ65SBovWk4xTNsqyJvPv7LZS77BUe5wQOY3Ghbov7WyznREVXjziP147KT9Mm7/SpF098kQV+SUg7mHzl89XUcvHShlV11DajqHNjqMY3/cfvT03I0tOxs1FOVGcjHOUnTRwlvJqkNqIYv3DFAf1JgNS5Yb3scwlj6YrlnpTVkG+l83L+53RdlVLx93ucSjbQAAAAAAAAAAAAAAAAAApz4YXMf8AJhcSNtPEONcVTOPPJTQbZVfqE2Cfw8kkbxlT9UWxXHmpmnqGnJKnoZSoJpszVOyikjkId0vp7UTUYxcC8ZuL64ojrjIrmYnZedquoreyKzt2qvJSD5Z412jG1Kqn8974BrzKxfR7lwvpTNbt8TqtGa3JSLcv7oZn4iqk8XaL3RSj+jWEm2FRQsfLxzlJ5HP0COWrhLHjKqmcuohi/dLiP5z7U5SLt3yppSoKEop3UEOm5O1O6RXQIQqpClMYu2cv1jlFx3Byw91KIsjhQ106XewLyn1+Ril3S6SnOGZ9opMNBzedG1F70xAEtgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAH5KJlWKYpilMQ28Uw6vkNH/8A2/sijvgAri4Jdg2cz+YTlm6auipktOsuBtO26FiKEa0aH1pNUUTddNMpRXtwR/0fzEeyZL37oWKgAAAAAAAAAAAAAAAAAAAAAAACu3Lf9VyzAex740aLEhXblv+q5ZgPY98aNFiQAAAAAAAAAAAAAAAAAA67lmg7IUq6KaxMOicuodgAEWOEjimTfJPc1RNogmcrZrpMRMpeL5tbjIMisWyXyhWoVVaNzmNBJYmOdIv8I8vhK/SR3Q+9Wvw1uPeyHek7tJ+A0vjAN6NmyDQmhBNNEu9pIXSOyAAAAAAAAAAAAAAAAAAADGrl+hzVX4KdfoTjJRjVy/Q5qr8FOv0JwEM+Bo9KdK+yl58HaieIgdwNHpTpX2UvPg7UTxAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABXVwR/0fzEeyZL37oWKiurgj/o/mI9kyXv3QsVAAAAAAAAAAAAAAAAAAAAAAAAFduW/wCq5ZgPY98aNFiQrty3/VcswHse+NGixIAAAAAAAAAAAAAAAAAAAABGThK/SR3Q+9Wvw1uPeyHek7tJ+A0vjDweEr9JHdD71a/DW497Id6Tu0n4DS+MA36AAAAAAAAAAAAAAAAAAAAMauX6HNVfgp1+hOMlGNXL9DmqvwU6/QnAQz4Gj0p0r7KXnwdqJ4iB3A0elOlfZS8+DtRPEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdXBH/R/MR7JkvfuhYqK6uCP+j+Yj2TJe/dCxUAAAAAAAAAAAAAAAAAAAAAAAAV25b/quWYD2PfGjRYkK7ct/wBVyzAex740aLEgAAAAAAAAAAAAAAAAAAAAEZOEr9JHdD71a/DW497Id6Tu0n4DS+MPB4Sv0kd0PvVr8Nbj3sh3pO7SfgNL4wDfoAAAAAAAAAAAAAAAAAAAAxq5foc1V+CnX6E4yUY1cv0Oaq/BTr9CcBDPgaPSnSvspefB2oniIHcDR6U6V9lLz4O1E8QAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAV1cEf9H8xHsmS9+6Fiorq4I/6P5iPZMl790LFQAAAAAAAAAAAAAAAAAAAAAAABXblv+q5ZgPY98aNFiQrty3/VcswHse+NGixIAAAAAAAAAAAAAAAAAAAABGThK/SR3Q+9Wvw1uPeyHek7tJ+A0vjDweEr9JHdD71a/DW497Id6Tu0n4DS+MA36AAAAAAAAAAAAAAAAAAAAMauX6HNVfgp1+hOMlGNXL9DmqvwU6/QnAQz4Gj0p0r7KXnwdqJ4iB3A0elOlfZS8+DtRPEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdXBH/AEfzEeyZL37oWKiurgj/AKP5iPZMl790LFQAAAAAAAAAAAAAAAAAAAAAAABXblv+q5ZgPY98aNFiQrty3/VcswHse+NGixIAAAAAAAAAAAAAAAAAAAABGThK/SR3Q+9Wvw1uPeyHek7tJ+A0vjDweEr9JHdD71a/DW497Id6Tu0n4DS+MA36AAAAAAAAAAAAAAAAAAAAMauX6HNVfgp1+hOMlGNXL9DmqvwU6/QnAQz4Gj0p0r7KXnwdqJ4iB3A0elOlfZS8+DtRPEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHADGJG4tJxLxVm/qeHZuktlRu5kUiHJ3xTG4x+Xy2aH/fnAflRD9YV72ey424vPd3MNKVtSraefNLhSLZBZwqqTSlr1adg5esNt+UNsJ63DD8acftRTs5UK5a5abJW/Laof9+cB+VEP1g+W1Q/784D8qIfrCKXlDbCetww/GnH7UPKG2E9bhh+NOP2oj87WbNV8FZWlPU9O39NJz8bHFdVGkdDB28TS5UupztF1G2hYF8tmh/35wH5UQ/WEUPKHWG9bmP8Axpf9qOfKGWE9bdh+NOP2oz52s2St+W1Q/wC/OA/KiH6wfLaof9+cB+VEP1hFLyhthPW4YfjTj9qHlDbCetww/GnH7UY85Xk2THh56MqFlzuLkWkk249PLs1yqk1d8XsD0xDHgx4RlTlDXliI5uVpGR9z5lq1bl3UkiJNSkL4uAmcOhhuAAAAAAAADgBiry5tHsHSrd5VcK2cJG0KIqyKRDkN1TF1D5wuzQ/784D8qIfrCujK9lltheNhc2erOk289KFryZaldOFVSG5IpiHKXZOXrnG6vKG2E9bhh+NOP2opy5UIS1y02St+W1Q/784D8qIfrB8tqh/35wH5UQ/WEUvKG2E9bhh+NOP2oeUNsJ63DD8acftRH52s2auy+VpTzThWL6yziejkopxT+JEHyzxIiKhtUb2CH1aTbpvFE/8A5bND/vzgPyoh+sIoeUOsN63Mf+NL/tRz5QywnrbsPxpx+1GfO1myVvy2aH/fnAflRD9YPls0P+/OA/KiH6wil5QywnrbsPxpx+1Hx5Q2wvrcMPxhx+1GccyvJsmdEy7CdYkdxr5vItT7rhosVUhvuGL2B3xDngtWaTHLXJNESck3b1XKJJE6hCql0lExhebgAAAAAA8yYno2nmfOpORaxrbDHTyrxYqRNXfGHi/LZof9+cB+VEP1hFvhL4RjVFP2QhJVAruKkbmxLN2gY2yokoRchy4+CbEdXyhlhPW3YfjS/wC1Fe26NXc02Su+W1Q/784D8qIfrB8tqh/35wH5UQ/WEUvKG2E9bhh+NOP2oeUNsJ63DD8acftRX87WbPa4RW4lJTWTG5LKPqeHfPFWzTk27Z8kqc/za33SlMPfyRXGpGKyl2tZvqohWbtKESIq3cSCRDkN2d4pjcYwbyiFhfW4YfjTj9qHlDbCetww/GnH7UPO1myVvy2qH/fnAflRD9YPltUP+/OA/KiH6wil5Q2wnrcMPxpx+1DyhthPW4YfjTj9qHnazZLKNuLScu9SaR9Tw752tspt20gkqc/elKYZPjxfXFZd18uturL3sy7SFE0s2gXzyu2aC6zdVU+tLe0bZzCzTsYi1CzFsdot3IAAmAAAAAAAcBx/wCvKq4iu74Zwr104jeCtaJg6VLE8xYU5I4oJ9vaYGPxl74urw8RkHlU63/5lbr/lgVp8iuEtZNNk7eP+AY5cVM61v6mTTJiZQ8Y6KUpeljyRhDXyqdb/APMrdf8ALAeVTrf/AJlbr/lgaeaq/wBmz54G9NRHKfJaiYk1VQ8MXVhvfM7cTv4xA1nlIq5ghyLbMbdJulvaUpUpSj9fKp1v/wAyt1/ywHmqv9mydvH/AABx/wAAgl5VOt/+ZW6/5YDyqdb/APMrdf8ALAeaq/2bJ24FAQxyGy9Vs7p35oioq3nq3Y0w+i0o93ULnnDgvKoKnPxm8EnigLOJdW6Z4AA3AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAEEsp/okZkvbKlPiiRojllP9EjMl7ZUp8USNHA5H2yQyAABTagAAAAAM4+Rp7g3/oJfr215v3jcTBEPuDf+gl+vbXm/eNxMEenx2rAAANwAAAAAAECsiX0oXQ9sOZ9+kJKiNWRL6ULoe2HM+/SElR5vkfbJDIAAEDUAAAAABnHyNQcF/wCl3m/ZhLfpSiX4iBwX/pd5v2YS36Uol+PU4+FgAAGQAAAQ84RTdy7+2tCf3o3GNOcIru5d/bWhP70bjHI53zFpIAAHLRAAAAAAAjjmo9FrLR7YbMTsw8zEQTzUei1lo9sNmJ2dEd/i/XhJHtfQAAuJAAAAAAAQXtj6fHNB3tP/AAISIEd7Y+nxzQd7T/wISIHn+V9kkMgAAVGoAAAAADOPkaRyW+mjzUfhOE+CqgGS300eaj8JwnwVUB6evswsJnAAjpmPzbx1lJJlSFNw69eXRli/7OpWPNxmJhx+fOj+pJf67BeMxdvgSEWWTapGVVOVJIheMxzm0lLgNN1bnLsfQzkzeZujTSTgvEUyLZ+V0cuPdFS1YlEbDZZa3vyqWXzBV49mElTcqWhqbXOyh2vcH07Spu692YbZpLLla2hmpEoagKeZ6PVfI5JVXw1TEOY3jilLlQj2tNnuRXCB5eZpyVBvdSFIbH/iyqti+OqQpRuilK6p6vI0khTM9F1CwNh88xbxN0l4xDYjSsraiiZtudCQo6n37c3qTiMbnJ7og1BUmR2g/JHyet86lLTVUXzqWpR0dAnhN9ekxe5JoGkeZD9jZOjsYjni7HEISUbmurrL7UbClcwyDZ7APVObxly4pHQ0VNx7BHqXqB+73f6jHE0mrpF83TcIKkWRVLgZNRI+BimL1i/1i7GUZesW7tAACQAAAAAAAAAAAAAAAABBLKf6JGZL2ypT4okaI5ZT/RIzJe2VKfFEjRwOR9kkMgB1JWVYwMc4kJN4gwj2peVXdu1SJJJE6xzn3RqrHN3Z49Sx9PNK8jpKbfukmTVpGa3XKqmPpIXWkQxd4VIwnNq3AAAMAAAM4+Rp7g3/AKCX69teb943EwRD7g3/AKCX69teb943EwR6fHasAAA3AAAAAAAQKyJfShdD2w5n36QkqI1ZEvpQuh7Ycz79ISVHm+R9skMgBjVbXOpO2jVFzVlSxdPJONXJHkHRUuV07+jVvDH7a5hbe3hmZKKo2pEagdRyRVnPNW6vJJkNu9tOTQI9JdN2rYoAA0AAAbY+cDUHBf8Apd5v2YS36Uol+IgcF/6Xeb9mEt+lKJfj1GPhYAABkAAAEPOEV3cu/trQn96NxjTnCK7uXf21oT+9G4xyOd8xaSAAYFXd+rdWvdna1TWcPCuyEKc7Rw8LzjQbd7VvDmYjv8ImegMStldalbxU+rOUfKeTEOk6M152VBVIhlS6NejWQmrfGWh06emQAAGBHHNR6LWWj2w2YnZ0RBPNR6LWWj2w2YnZ0R3+L9eEke19AAC4kAAAAAABBe2Pp8c0He0/8CEiBHe2Pp8c0He0/wDAhIgef5X2SQyAABUw1AAAAAAZx8jSOS300eaj8JwnwVUAyW+mjzUfhOE+CqgPT19mFhtvNpmCJl9thhIsGuExWMy5LE03EYY7Tp+rsk2eqTeN4vSGqsudgcLURb2oKkd/JHcyoj86qGoHO2dVQ21ySR+ikT4neEJj0gvjfXPxUUg6+aKatNHJRsekbcxlHRdSqvfFLs+AUSJHL5dvu8NpJ+LlDnLVVDUoTlSmJrRNoOTvDisrMjQ5qhzsUNaun6nqiQjHhWSsu0kZx09KTHWZVXTypzfuchTizg5ykKcxjaCFFeWSMny88492burl5ZkxMqhHGP0eVPySPiIJe6EPHxriUmkVh5CFITSXdKORGW6PCH2etZVRoFeSkJ56iryTk8I3K4SbG6eo5jkKfwNYkVT08xqqBj5qKcleRsigk7auCeqpGJqIfxRWnCcfWTL8qspOJrenX8FOx6MpEPk+SctVy6imKNH5YKxl8s94UrAVXILSNIy6SrygZl6bbKQvnsac3WJ0f/eQhZCjQmdSg3NV2Se1BDHM1q2i1SVPDvEt9JVrtn8YmvY62gWeNbrLoxFNsBhVm7iNLuWppKs2hSkRnYxu/wCSLjx8kc5MDGJ4JtRfBGajupgAAAAAAAAAAAFdXC1XlrayT+zk/Q1SPack8F5TAxmqmwuXDmmwqkbYVL3JymwAWKgKwcuXDHxckZtD3kh/Itxx6PkkhEjHbn7pVvvE74mrvSixag7h01cqnW87Ss6wn4hbsEdR7gqpO9x07pu5AQ6yn+iRmS9sqU+KJGiOWU/0SMyXtlSnxRI0cDkfZJDJ8HIVYpyKlKchugcVz2tiWd8OE6q+om7VAkRSfKn1JE2VF0CEakP32Kuo/gCdd4K7Qtfa2qqsX06YmOXdFIfpnKTYJ4ZtBRCbg714iztgq4u/WLvBqnNyfIlVxLrVcFS3SpF6Zzqqql09yNuP7YSkRWEgK/LzZ9ryWoqCnpeVtU0piiJZQ+LNtMqHPIOkiaNerSr2g+g5NgxOl0hP1ssVy1SXLqIRUpD7YrzqnD1H7AACLHy1ae4N/wCgl+vbXm/eNxMEQ+4N/wCgl+vbXm/eNxMEenx2rAAANwABWZwrF/K/sJda1UzQtSvYB0eOecuiifU3caVUtlVI2wp4RQFmYCtLLpwxdPVIVrDXeifkZkMccC+T0QQ6rE/dKJbSqXg6/BFh9I1lA17BN5qmphlOxLoupJ7HrlVSP4RQEKMiX0oXQ9sOZ9+kJKiNWRL6ULoe2HM+/SElR5vkfbJDJrfMZV7G31kK3qJ8ig4Izil+SScpFORVUxdBC7XWMcgjfwVFuPkZsVK1UulodVLIm5I/WbodqJ/1ecD8OFXr9WKtHTVFMTGPIVLJlOdEu8ZuhtaP7U6XiDaB67SyxWwoa2NMU+4rW4ZIlJNtT0YbRuk7a6XV3UkuV1bRt4WIR/g1/sz+qR4CF+W7OTcauMxsvam5FKRcJJIpqmISM1a2qqRNegx+VOUxTF6RRNAVZVSr9JAAANMfOGjUHBf+l3m/ZhLfpSiX4iBwX/pd5v2YS36Uol+PUY+FgAB1JH6HO/5I3vRkdsBRLlx4UG69kOaxU67+T+licReZTCpudok/inW99bzD6y96LSsu2fO02ZLBuzgpssTUimG1T8xiVB1q4vU+ir4BsQGGcIru5d/bWhP70bjGnOEV3cu/trQn96Nxjkc35i0kCH3ChVexprLgeKM2QVkKglG7VLE6ZTGJyXbTnL4hS+EJgiu7OdqvvnZtTadLt8ZGckvIpfyp+Vcf9BInjCtxo/ydWkUtMptuMLU5daFp9RPFF0WPK6eEx+3r9tV8Qx9HgDbojreLMlU7OYlqTs5RRrg1LEE/2m7OryUZGH0+dGNrJyqv8UU48jItmvnMz9PVThUsUyYS8IukUy0eQ5ElSK6tGwcxtJi8kbpDWdUpY8VlKEAAVmiOOaj0WstHthsxOzoiCeaj0WstHthsxOzojv8AF+vCSPa+gABcSAAIOcLBcSprV2Mo6oKQnH1OTCNVoFK8j1zJG081d7JuLeL3JtkBOMBU9ly4ZB4yxaw15obniPFo+SWFS0K/X2lm+6bvktPmbgsptdeGjL0U6nOUVUjGoo43FqOzV4zJG4uPSqTeTN3J8MMQET7Y+nxzQd7T/wACEiBHe2Pp8c0He0/8CEiB5/lfZJDJ5lQxryYh3DNjLuYF2ro0yDRJI6qW30CKkOXxymEBrT1jcatc/ElRCly56oqOpRddy6wMcrcipUiFLyapEClKbS4MQm7taBO+u6tbUDRNQVK++dYliu9V4uqkQ5viCE3BYUk6lYm4l0JjHFSQn5LmhXB+lp7asbwjrF8QZpxrVKTKewDTxs4FnS16hRpK7jl59ZfmxUkdZ0cFNzTzghOS1eGNwipKMo9zQAADHyNI5LfTR5qPwnCfBVQDJb6aPNR+E4T4KqA9PX2YWGMZJDeS7C8FSqYanU3cOZcKn7gpiaCe/ElRG3J0X5GagvpRa+Ol1CXAkXBCH3+br6TIm8PQYSSHC5H2yQyaazf3I+VXlvrqcTV5F4diZk0P0+XX7UXxNevwBEfI/SUjVNmW9vqfeLxCM0ueZrKea46VWrU3am7BI/RVVSS16uiU/WOQZDwq1Wu5dnbi10RhivKT0hz3FuTfN6g3L4ZlT+IJb5f7LxFgrWw9IxZSnOglyrx303To3nqpv9bhCCTH8VH/AKZ/VC3hJISmqJoC2dpKKp9lHu30li7QaskS4GKUpOSJhq3jGOdXf6WgT0tpR5be28pel0jcsSGjEI/X1+SSIXX7gQFZP22YThI5edfLJYUlbhA5zuFjdqS5ns6tX30cx+9KJxVbemmqSXhGOp3MTEylziOiYlqdw7cJdNXR0S92fSULttYxayZ2OlPRvkxCSEeUxSHdNVW+tUusm0TRtkHg0BcuBuWwduYVdXlWC52r5i7SO3ds1y+pKpG2imHq1VPIUrS8xNPDaGkczVeqn6pEiHMf3gpY72FfmUi12butbIRa1tLuwlN0eycumDOMfm7akZNU2v8Aciuzr1dMbk8rvn79fql/Gx/wA3jwaNPOKfya0Mo7LiRzJmeSZy9yq6VMT3GgSkHqMfCwrq8rvn79fql/Gx/wAeV3z9+v1S/jY/4AWKgMiuryu+fv1+qX8bH/AAAeV3z9+v1S/jY/4AWKgArq8rvn79fql/Gx/wAAHld8/fr9Uv42P+AFioAK6vK75+/X6pfxsf8AACH3CFW4v/QLKhTXur6LrZN0o98iix3Z5riXkOW1/M6W9qS626L1hBrhIcp1c5sZW1kVR6LNFvGqSJpGUkXHJJNSqc1wJs7x9Wg+6XHdAUeCX+SLL7mQqWp2lR2nXkaKizGJipUT45m7BYvY80hi8Tovc6DlFiuXPgtrV2WxaylStvlh1Qlt84lUvmJI38U13fH1+CJnIIEbplSSLgmkUukpS9EBAXJU1lI+o7+NZt8hKzSVfvyPnrdDm6S7jSXWcqWo2kpz9ESgEcsp/okZkvbKlPiiRo8/yPskhkhhwqFyPkWsCxpdBXk3VUSJEjl6zdDtp/dc38YerkxtWepKCoWo5xmZOmqcYlSpSIcF2DODbbiVOTrKqnPyXULtdMaczSx2GZbP3QtsTGOtCQSCXkgUuHRMTnTjxkipFFhr95H0lTjhyYqbOMi2plTEIXQRJJIn6hBLLOlUYMq+c1nHmOz5W8tYlhzmHp/QpIl6G380OP8ApESJ3wsWFZeRKrk6gutcu7Umh5MVbOPsY+Hg26xecKnXPyq2PcJJEIl23dKXUJeUHmJnKtzLztrpGjj023iYPyU5w7clVcONSqRSedHOUpdCpumbcGL4yz7cfqxJvgAAUcfLVXfl+tNmhrGUu24tJdCEpSFQr6WbyKD3DSZd+UxOVVIXm6uyYhkul0Btvyu+fv1+qX8bH/ADanBv/QS/XtrzfvG4mCPT49IrCuryu+fv1+qX8bH/AAAeV3z9+v1S/jY/4AWKgNxXV5XfP36/VL+Nj/gBCfhBqAvhQdQ0aleytoytHrhquaMVjvUEinLrKb5nS7PZLj0hfaIE8Ifk1rrNjc+3SdLYMmURFs3RZCYkVtKTfUolpIUhds59k2PF5ndFAUmibmRDL1mYkqga1NbV7IW+pxY5FF5iVMdJg7J97m+evExL3RRYbly4Mq0tiObSUkx+Tyqk8NWMnNpFMgkf+Kb7hfC1m7oS7wIUpNJd0BATg/0XaVvbipPVk3b0tfSxF3CSfJEVV7VrOQvQ7wSfEasiX0oXQ9sOZ9+kJDz8w2puDkJV8ryLJggq6XP1CFJrOPPXetskMlZWbS5OFY5+qajEGCtQp0pi0bsohttc9ffPBUu5wMqZIhzdEpTfYE87aUG2s/Ss3VFUPk39Vv0jytSTxy7xik16CdRBIuyUnVIIbcGzRPy07p3GvZON+VdmkVUmJzbXJLr61XBi94UyRe8Ocb34R65p7d5Ypts2V0PajXShUu8NrOr/ANIhyeGLFmfdCmLLS3BwxDq7N57r3slUjYGeOjsmmrHdOuflTl8AhUieGLCxEDKPU0DY/LXEMmzReZ5rE+Tk07jNKvze5MQzdkTT56uYhiE0dDQTVvEH511mlvtaRsnV1ZWaj21AcoXnRI+VIvIM0zH2DK6T6fcae6KI7Yyts9omGOFN3ZHl0pU0fWlMRVQRK3OI2TbJPWyvWSVLqKPVFPGOkujRXDlPtDmuq+3kq+tXdeBpmmPJ5+iZk82DGdFP21XTzVXZN343T5XfP36/VL+Nj/gBtbgv/S7zfswlv0pRL8eox8LCuryu+fv1+qX8bH/AD83WXrPqVsqZW/FMHS0m1F1dH8QFjI6j9MyzJwUm0cyZilGR/LEMloiiKluDUTaGpWGfzkypj2lpGoGVV77Z98LEMufA5TUzzWZvBMeQjPHDXhTsMoVV0bs7qq+4T7hNffFFmVprHULYuALDUJTDKAaae2Gbpcay/wBgyqpttQ3fGxAVmTNr8wVtaRsCleSrUpOKPc2DJHwTpbnj5mbjV89c4Y7unUXRqP3xeLSLFBpzhFd3Lv7a0J/ejcY5HN+YtJPg5yolOYx9BSbZjnFT1hKvnr15wLh1BSmr5Ip87hrHyhyaiw7AxsCned8RBIqRC9ZYon5nHuP8qzLbW8ykryL1ViaPa9flV+1E095r1eANV8GbZ9vQFgG9UOGxSTVVKmdKqnLtkakMYiRe97Bj/wBKIqvZVKbVnV9pGEyqZTanwptLmJWzEzJmYxtayr1fY5UxumrrPypjdwMK4Mq13yCZc0JxylgSQqh4eSNq3ubl7Ul705/DGsOFGq1xU9R2xtMzdJtTyrwj5ydU2khdZ+btzG7nbW/qEkGFyJCKoiNp61NHGqQjUpI2Fdu3XN49VqgQhDujq/atWwTRtK7ZibG0HTOKv/Q3sAjZaHMpWzy9i9qLqUgypyqFWJpGNew65lGrxMu9vY9wbxT7okmKs4ZgIh5/Yer56fsYyoqYbQlRL1YRvHunBdhB4YvzOqY2g+yTa6Bt4fv5XfP36/VLeNj/AIAZPmo9FrLR7YbMTs6I7XF+rDMe1XZ5XfP36/VL+Nj/AIAPK75+/X6pfxsf8ALFQFxIrq8rvn79fql/Gx/wAjVn6tdmXoe0cO+vRcqGrGmlJpJFqyjeydN3yCulXH5lS6BVel0hdUIhcI9l9rHMtaSlqSotm3cyBakSeLrPFipItm5W7gplTG83TqMTdwMba8wBQoJJ5Q7GX8r+sGs3Z5vKwOKB9ClTprnZsk8OkQ6vqvdJE149yLHsuXBJW4tidrL3BW+WDUBNvmipOSjEjfyW8r4ez3AnRGRrOIYIMmDZFkzbl5NJu3SKQiReqUpd0BX/AJYIqq4XNbmAZV1NtKiq1BCnySMkybcgkurzI26XvdP6pdwSvEd7Y+nxzQd7T/wISIHn+V9kkMkSOE1uP8hWWxzDoKYEe1M/SjS6d7kidtV94UvhjHLC2+fV1aGmrRRDxeHo2EZkNWUsxPpcP36/b1Y1I/Q0croVP3hOuNXZ/wDCSv8A5sLeWggleJVo3Lgqfe5uqvtqnN3iCRDiwOgKGg7RUHH09FE5tFRaG0sqbbP01VVT9Ixz6zGOJ5fx1RwyrizU2io1zm3tLay3lOMIE6RW3kgeMS0HxKZXViZU++c5EkzH1H2toWiiufJCYt8M190L2SxykjWap20co42dBnBuSSL4Lcmj+kFirlykzbqrrqlRRSLrMqc2ghCdcacr9YsSfYDwqGrmBuPTTSoaakk5iEdGMRB2lr0G0nOU+93RTj3RR/y1aRyW+mjzUfhOE+CqgGS300eaj8JwnwVUB6evswsPGvQjhl3zrQ9bK44NqMum0Sg5Fx6khLIfO5z9+TZ8cSHHr32sxA5gLYTdFVCU5Wb8nanaWHGqzcF2kl0+PpFN2f4d0RbsbeWeoiq/lLXjMVhXscXkomZVx0t6ja9BVI5t9XrF3vD1jncqnr/JFpKLsVflGQrzNDB3el6nM5bwhUiM6e5hsF5Ip9HbeV+2n5XdEhQAc2U5y6NURbEZBCWormpJmbrNxUUNKucHBoYiHIJOsSKGUSxdH1n5XSc3Ho3DdLVuDjKzMLXEzaZhanf48qtDO0KeY4n9QQSOqQ5Cd8ZIhhLsRLy7QZ7TZv73UvIl5ElWGQqaHMfcXS1q8ro7062nwBPi2U4y2H5KTClCcJQSKZ46GdaUkVV+mTdOuhyuhXvtLfT4YynOlUkhO0zBWephTlKyuQ8LFJEJ+5WevW7XP3JSbPeGP1Bpu511KcpLO/UFyJdzitD0RAFg2zdptuJGUV1G5q3J0jaXB9fU6Qk9lEsRUq1VS18LqtOb1/UCODaMhjYbNPxvRQw4/VDdP/8Akxhbrp2lGbbVJeiqRYUJSMJTUUlyMZDsUmDUnVSSIUhf/Qo98AHUbgAAAAAAAAAAAAAAAAgllP8ARIzJe2VKfFEjRHLKf6JGZL2ypT4okaOByPtkhkwWBsXQtMXFk68jKfRbVbKFOV5K8qqcypTade8fQXdLuDL5WNbTcc7j3yBXLJ0kduukfcVIYmg5B2wFXfLVrKzuW63VhivPkLpxCLcPOwu7Oqdw4MTqajHObT3A0/S2H/6lFZY//sRD4Q3ErREOlplP/wCoHU9RHYyhKee0knFN5U8auVqq65VE+nlNOnomFmvMp7dW6XgAAq4+WjT3Bv8A0Ev17a837xuJgiH3Bv8A0Ev17a837xuJgj0+O1YAABuAAAAAAAgVkS+lC6HthzPv0hIKp6bj6wp6Qg5dtzyKkUDtXTfUYnKpG2Tk2RH3Il9KF0PbDmffpCSo89d6WyQyYvbi19LWkp3yBpKJRhYflDL83SOc/bTbxts+oebd+yVG32pxvCVpF+Skeg5K6SIRcyRyql2NWopyG3DnGdAK2Jy33asfpW3tOUTS8fTkHCtI2FYaDoMUktgpyn1kP32vb17+sa0zZuV5i00hQsQgV5VFaf7FjmnfeeuDdRJJLWYx+86w2BdG4Ta11FyFQOYySmOQL2qPiWZnDhdXoEIUvv8AdET6Hzfpxkg6qao7Q3PkqtkC8kos2p/5nZt94jVDUfc6x99U22bolJaqjOXvbpcW7o1tbihKdpZkYyzWHYoMElj75+SKQusZGMStTV8lX1CRtRSsItTjiRKdwlFO/nhBLWfkuV7rRoObq69Iy0V89/q0ag4L/wBLvN+zCW/SlEvxEDgv/S7zfswlv0pRL8enx8LAAAMgAAAh5wiu7l39taE/vRuMac4RXdy7+2tCf3o3GORzvmLSTErlWppO8VPkg6wiE5qKKuV0VoqqqQnKl1kKfYOTrnHvwMCxpiDj4iKbFZxrBArVq3R3Ekik0EIO8A5u+fhE1bc3LLbW81XxFS1jTSc3KxiXJIHVVVKQ5NeshFSlNpMXUY+91xsdYhoqLOWPYlW5uloQaImKkTZ3CE6JR2xrW6V+6ftDNxEfUEbPHbyBDHLJxkUq6aIaegqZLUcp/AG/Wc/a3R+o27j5tnU5tdWhFqSqaXjPIqknhHhXTQjUpjqmLrKTbVVP0+8LoLvGmWI71HCJ5irv21noyMetqXotyvKnmZFiqyO6XMQhUm7cipCGMXXtHPo07BCCRA3tz11Ecc1HotZaPbDZidnREE81HotZaPbDZidnRHY4v14Zj2voAAW0gAAAAAAIL2x9Pjmg72n/AIEJECO9sfT45oO9p/4EJEDz/K+ySGSLNpMp1R0zmvrS8VXSsXJeSfOCRTRidU6rUpzlKTXqITcbl0bPWG+rr0zJVpa+rKfh3SbKTlop0ybOlceIiaiqRilMbxxlgCCVs5SxJlEXJxlAqezVKFj68l4940Sk/JdrCRhNSXOtBCEVcKnKXldGjZJuENtbRtGjYl7HK91z1BQsYuqjTkQxM4ql8ibRyp+S1JRpD9Y+wdX+K0F9VG46nJKnpyVLBmbEmzNVeYnd+dEcaO1a+51aBEqPpTNDQNuJGIRZWqVYFaulnrpRaRO7dHOU51Vzn6aptswnhLxp7SGZ8HT6UCh++e/DVRJUQ84NQ1ffKOgiyKVOkt/yDryKM0M4wkzOOdH18vr7Vo893e4EwxHd9shpHJb6aPNR+E4T4KqAZLfTR5qPwnCfBVQHoK+zCVM4atvvl7ovMRRxoGsInnZEjYrM37dTknbBX7agrxcZDe5NxbWA2kAkEE16JzJZaO0MUEL/ANCoedHO45rUDZLqm1bK/uzm7gdTy/tvIJTFCuoar7cSBNhVvUkAuTSb+iIYT2/nH5nTKcuk2BTF7oVpceufy01QPW4RaxZzkSjKlkJt2bdaR8K8MqfxkiDG6uqa4matJoyoiwb1s3SPrbVfcTXFkZatnlUClNy5v6I/gCw5tHt2eHaG6aP8mTSO1xfwjSPFrh8GqI2WHg/6WsfKNqtql0WuK8SxxMg7WblRZRxzbR+at90puP1Xe73a45dAAuNwAAAAAAAAAAAAAAAAAAAEEsp/okZkvbKlPiiRojllP9EjMl7ZUp8USNHn+R9skMgAAVGoAAMgAAGPkae4N/6CX69teb943EwRD7g3/oJfr215v3jcTBHp8dqwAADcAAAAAABArIl9KF0PbDmffpCSojVkS+lC6HthzPv0hJUeb5H2yQyAABA1AABnqAAAzj5GoOC/9LvN+zCW/SlEvxEDgv8A0u837MJb9KUS/HqMfCwAADIAAAIecIru5d/bWhP70bjGnOEV3cu/trQn96Nxjkc75i0kAADlogAAZAAABHHNR6LWWj2w2YnZ0RBPNR6LWWj2w2YnZ0R3uL9eEke19AAC4kAAAAAABBe2Pp8c0He0/wDAhIgR3tj6fHNB3tP/AAISIHn+V9kkMgAAVGoOu/YJSrBwzXLrbrpHSVJ3BtkdgAGK2vtlA2eolhSlMNlWkKx5XkEllTKnLrOc59s3dnOMqABnr1y3aRyW+mjzUfhOE+CqgGS300eaj8JwnwVUB6evswlTOAAG4AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAgllPx/wDyRmS9sqU+KJGiFlE3blMvN275sZq1FxZok3XD+VZuoCnjOG6qBj7BtZjE39/YGd+XhQ9ZG8f5qf5o4t1NkrJSjFDKKTACM/l4UPWRvH+an+aHl4UPWRvH+an+aIPL2f1NUmAEXo3PtEzGLorG0V1nhmq5mjrm9NYK83VLvJH0q7BtouyOz5eFD1kbx/mp/mjPl7P6mqTACM/l4UPWRvH+an+aHl4UPWSvH+an+aGOPZ17TVm/Bv8A0Ev17a837xuJgiIPBvxksjQV0ZeXp2WpvCoLhSkyyaTbI7Vxi3VSb4lNpP8Aw6i+AYS+Hdx2pgAAbgAAAAA4AQLyJfShdD2w5n36QkqIPWSvLKZdlLh05UFo7lyzp5WkpJpOIWnDuG5klTlwJpOYxNW5x/zjZPl4UPWSvH+an+aOJdRZOyWcRQ6pMAIz+XhQ9ZG8f5qf5oeXhQ9ZG8f5qf5oh8vZ/U1SYARejM+0TOIKrR1orrP0k1TN1TtKawVIRUptJiH0rbxDbGgdny8KHrI3j/NT/NGfL2f1NUmAEZ/LwoesjeP81P8ANDy8KHrI3j/NT/NGccezr2mrOeC/9LvN+zCW/SlEvxEzg1YKZp7Lq68nIWSgHL2o5F6kzlWp27jklVC4kMYhv5/6hLMd7HwmAABkAAAEPOEV3cu/trQn96NxjUHCNR8wakbSTkVTsxUiVOXAjJl8zg2Z3TnBBIqpjGwKXDwe+MUYN5eBD1krx/mp/mjm8quVmY6tJJMAIz+XhQ9ZG8f5qf5oeXhQ9ZG8f5qf5oo+Xs/q01SYARef59omHM1K+tFdZmZ44K0bc4prBLnCpt1ImpXbNsm2R2fLwoespeP81P8ANDy9n9TVJgBGfy8KHrI3j/NT/NDy8KHrI3j/ADU/zQ8vZ/U1drNT6LOWj2w2YnbgK0KruvKZhr0WKbw1rbiQaMHWLWTeO5+njt26SBd82shj+7Fl+A63HhKFeIybxcgAC03AAAAAABBe2Hp8cz/e0/8AAhIgRKY3boy1eerMcasKkjqcI/8AIHmuMiuVLldDLb0+OQbY8t3ZX1zqZ/KJRw+TXPNnXGEMm3QGovLd2U9c6mfyiUPLd2U9c6mfyiUVfCn/AFZbdAai8t3ZT1zqZ/KJQ8t3ZT1zqZ/KJQ8Kf9Rt0BqLy3dlPXOpn8olDy3dlfXOpn8olGcVT/qPOyW+mjzUfhOE+CqgPKyEVLEVnmFzOTUJINpWJeyMMdu+aG1oql5u4Lsm/mAehr7MJU4wABIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAANR5ob5MMu1janrp1pUcMUeTYNzY8fOHhtlInjY7XclMNuCmPhfMx2Ne3TY2uiXWuEpM3OJDQbZVkTk3fN9SSNp746oDjgrc1L+m8wM1SNVSajllcBwZxzlwb/e20cpvuq8Zyd0bkhc6P5Z4qXdwUk0kY9wo0fM1CroOEjaTJKFNqKYv3B/RjlKvyzzIWGputW+KScisnzaVbE/c7xPiKsT7mO+XuTlAbnAAAAAAAAAAAAAAAAHA5AAAaEzrZgkMtmXuoqoSUIWbXLzCGSNhvvFdw3gYalPAG+xR5wruY/5bt+MaNinXLU3RetlsH2VX5vng/g6SpeAfrANj8EFmbXhbhzdq598ZRpUpzykaqufVjz8pe3E/pUi6u+R7oW+D+XOjaskqDqmIqKGcmaSsS7SetHBegqmbAxcf68B/SHl8vFG39s5S9dRWBUkpZqU67cmPHzdcuyql4JymL/MA2SAAAAAAAAAAAAAAAAAANK5uL+NMtthqkrNUyeMmilzWKbn9WeqcZUi+Dvm7khgFZPCm5rH9Q5h4elqTlFG7O3jorgrlub/e2yYxv6LSQnfcqLR8sd74/MJZGma5Y6E1X7fS+bl/c7ouyql4+73OJR/OBJyjqckXcg+XUdvnShl13CptR1TmNqMcwsD4IDMZhRVz39rZZxpiKoxwcx2vHZSfpk7Jf6VIvjJEAXKgAAAAAAAAAAAAAAADX9T2LtvW0yrL1Hb+l6glVSlKo+lIZs6XNp7Bds5MTDoeVes360lC/m2y/ZDZ4ANYeVes360lC/m2y/ZDzKhy+WLpeCkJqVtdQbOMj2yrp04VptloTSITUc5u1dUo3EK7eF+zG4ULa1ha2Jc4EmKrw5xIYkx2kmCZ93+lVLp71I4dBHbJdeu2Vys5FUQ9U23o4lK1utyUAxdQLMyUYql2G6RS8npJiqlsH07yuj7ItM8q9Zv1pKF/Ntl+yH828PLvIKWZSce5UaSDJYq7dwkbSdJQptRDF+4bAf0ZZTr7s8yFiKarVHFMj9yjzeTbk9QeJ7KxPuatsvcnKHQet5V6zfrSUL+bbL9kHlXrN+tJQv5tsv2Q2eAdBi1HW3pO3LVwhSVLw1MIODYHWSho5JqRU/WMVIpdWIDKQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB5ssR4vGO02CiaMgZI5UFly6iEU07BjF6RdXEKup3gXanqedkZiUvO0eST9dR05cqwR9aqpzYmOY3zR1sRauAChnKpwe73NE/r9s2rVvTuNJyRY4x1Y4zjnWrldvz0unzr3QsryOZL6nyeq1IzcV+2qqnZjAivkeWOM2xQcl7HKlNiqfeJsm70nVGpeCP+j+Yj2TJe/dCxUAAAAAAAAAAAAAAAAAAAAB4VWMJWRpmWawT9KMml2qqTJ6ulypG6xi46FTE6Wk21pFXrrgS52QdKOXN4Wiy6pzKKKmgjmMcxul88C18AFDWTXg9nucGhZqpG1bt6YLGSXkadBWOM65XHkiKa9WCpOLf8wWgZIMpFSZRIGoKcf1y2q2BkHBHrVuWOM3M1X06FTeemwxKYuBPFGkOBO9AGufZN/wCIgLFAAAAAAAAAAAAAAAAAABEDPHkuqbOE8pxs3uA2panIYplCx5owzgyzo+PFypjcqTzCYFKX7HGfrCX4AKGs0vB7PMsc3biOc1s2qPGsZM0aVVKOM35ppMiXVjhyh9XnvuRI6n+BfqalaijZmLvO0aScc5TdtnCUEfUkqQ2oh/njrFGxOFj+nzLV7Jlf0rIWJgOhFldJxzUj5RNZ6VIvLLJF0kOppw1GKXq8Y74AAAAAAAAAAAAAAAAAADg27iKX8zeSvNJmLvhU9dOqAKRB8vybFuedYYYt2hNlJL546vFq7oxhdCAD+cehcnV1rlXGquhqfpgj+p6XMYkqyxkmqXNzYH0b5ldBtrsbJsRY9waFhL95aKuqCDrikcI+hZxHBzi4JKtV8GrxPdNoIqY22TjKbvCD98jv1QrNP9+K/DTCxMAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdXBH/R/MR7JkvfuhYqK6uCP+j+Yj2TJe/dCxUAAAAAAAAAAAAAAAAAAAAAAAAV18Cd6ANc+yb/AMRAWKCuvgTvQBrn2Tf+IgLFAAAAAAAAAAAAAAAAAAAAAFdnCx/T5lq9kyv6VkLExXZwsf0+ZavZMr+lZCxMAAAAAAAAAAAAAAAAAAAAAAAAV2ZHfqhWaf78V+GmFiYrsyO/VCs0/wB+K/DTCxMAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFdXBH/AEfzEeyZL37oWKiurgj/AKP5iPZMl790LFQAAAAAAAAAAAAAAAAAAAAAAABXXwJ3oA1z7Jv/ABEBYoK6+BO9AGufZN/4iAsUAAAAAAAAAAAAAAAAAAAAAV2cLH9PmWr2TK/pWQsTFdnCx/T5lq9kyv6VkLEwAAAAAAAAAAAAAAAAAAAAAAABXZkd+qFZp/vxX4aYWJiuzI79UKzT/fivw0wsTAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABXVwR/0fzEeyZL37oWKiurgj/o/mI9kyXv3QsVAAAAAAAAAAAAAAAAAAAAAAAAFdfAnegDXPsm/8RAWKCuvgTvQBrn2Tf+IgLFAAAAAAAAAAAAAAAAAAAAAFdnCx/T5lq9kyv6VkLExXZwsf0+ZavZMr+lZCxMAAAAAAAAAAAAAAAAAAAAAAAAV2ZHfqhWaf78V+GmFiYrsyO/VCs0/34r8NMLEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABxxgK6+CP8Ao/mI9kyXv3QsVFdXBH/R/MR7JkvfuhYpxgOQHA5AAAAAAAAAAAAAAAAAAABxxgK7OBO9AGufZN/4iAsUFdfAnegDXPsm/wDEQFigAAAAAAAAAAAAAAAAAAAOOMBXbwsf0+ZavZMr+lZCxMV2cLF2a7y1eyZX9KyFiYAA44xyAAAAAAAAAAAAAAADgcgAAACuzI79UKzT/fivw0wsTFdmR36oVmn+/FfhphYmAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA4xHmy0uygo1zIyTxBgwapmVXduVCpJJELvGMY3YKUJmZY09EvZWTdJMY9kiZw4drm0kSTIXUY5jY9HDDAV0VLU83nzqNV9JKPYWwkc6wLGQ5DGbrVEqQ3zw46XJ6t0nx9ob11ytlrFBddGiO0m1Ky4QN9V8w6grD0OtcBRA/JLVRJmMzhW5u5Nvr/X7BdHc6hhTwmZqu+3VBeyPo9M/mxtJQaRyE+4ur20bOiIdjT8W3jY1mgwj2peSQaN0ikSSJ3BSjujt18KuHe8lf+Xun6VeiNNvMq1d2ZXl3dA3vmqeeyy+Dp8fyJQXI6V2tsxDn2t442XH31zPWmNyk5GU5eaDS7Kp48vkXK6evp86N3pCHGywG8uJXJDX+U5EfnLPbAZtKBzDJuGMK8cw1Us8OJ7TE0nzaQbcXFq7X0y4dYvH/DpG8C44fWEALvWGjbmKtZyPdrUvXkYblYqqI3tThBUm5r0bxe5G4Mo2ZyUuivKW9uE3QibrUwQuL1FLHSjJtug9Q7k2zqw4tnE2Hma9JePdTKp6ni8yvkx/6ShHI4HIrOiAAAAAAAAAA+fMHydTAhcTGx4il83EfXm4iAeZC7k/mZuPMWcoOVXiKDhjchWVTMuwo6U4+zHNzfd3zfwG6OGk+0ISnLWKKyyNUdpM8unn0K5qN7R1kqd+WZU7Y3JO5blOShY838Yv6r3pOL6+2NWyFGX2uefBzXl8pSASVx48YegU/I5JDHqFX88N4Y2PRdEQVvKeawVPRqMXFti8ZW6RfN7s/XP3Y90duvhRj6zeT5H5WyfpV6I3UnkTpCjWqqEVWFbMMTKGU1MpnBt+jIUoyZjaq71vD8vb2/lVY4JbkdWOmXbqdzrPuF7wg3WAm8tV/VQj+Q5Uf2YlRWe6ftvKsqfzBUonSxHCnItq2gjHXiHBuP1UuO2h4XikKJlxkm0mGCD5g6ReM3CZVUHDdQqiSpDYbJimLvF/hEU5uEj6kiHcZKsUJKPdF5Jdo4S1kVJ3ZBpu2ddSWROvWEQ+eupCwdQPOQTM6OZU9KulD9f7Qb/373nvLv4vh+6L0fC/I4v/AI7O5ZEA/FFQqyRVCGKchsNRTFH7Cg7oAAAAAAAAOOMBwbsiL17c9dJW4qVajKRin1zrhFxxIaDgfOmpux89L9kqX8PFqMXpYFGv8zt/6mutcJ/ZO08ieJKwLprGsEP93EN+5ED/AG83ZwN1fBPiX7tfaamLQ06WGpqPKzS313Btpw6N11TdIwuUcaVvucfm8+PF9se5pu8dvL3ZuJOmZSupClreN6feHfRbGIbGfump9jj5Uxj6Tm2C9zsjMcLY3oP2w+ZSrec/ZIzRIl4nGNxgOpHiVPOy/KcmX+WqWNU5qbbGwWj6/pu6LJLej6iiyMHBi9UiqHS7o5xti0Ofim6sqNvR1xYJ7aiuluwkxmz4GZOzcf7ndYbJvC08fHhp1D5GL3DttTV1adcQlTRaMowU3MTb6R+uQ+8Uwht4cZdi3R+Wsjnpb6pr8fYDzMBAfLxe+pct1wIi0NypZedouYU5vSFXPTcaqKnQYujfd2Sm+JuT4w7OA484ShLWT1FVkbY7RcgADVOAAAA4HIAPnzAx7GAceAi1nGzKS9uDQ9t7eFTf3Vqkp+Z8rtJRLXs63qve7Wj62wbHa0aTZ+fRHKWIY2k97MDnPo+xr5vTjZq8rO4DwnGzpOFLgZx2d0yxvMRL3219goj9J1JmavSdRabrePs7CLbkJS7Yrp7gXj3VXRtw3dJH8AepZ2yERaVk5ccspNVVIm5xL1E/2nT5U20bUY/Q1dEbGHZq4Uf/AKPK8n8vKUtKEcY3I3SzOWfy69bV08nZE3KPpPGa5JV0be1mOUmo3hD3G2XeqqSNgtRF9Li0+4JtlSfSfkk0/sDaCnG8gFny9X9XN8/yuvc1tEZq75WFMXC6VOtbnUgl57U1Ko8hINSdddruG8HTh3Ql/aq71I3qpFrU1GTaE3FOMMO2Im4jpG6ihN4hu5N2RokaGq+kKgy6Vg4u7aFDAixe21NR6Wy0mGpd85SdFcm2fUT9cp6F/E190Xd4f5TeXh3LKPNwAYPaO6kDe23cJW1MuMHcPLIYKp9dI26dI/VOQ2opu9Act6NnIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA4xHI4x8wBCfP5Vz2u6moqwUM5UQ+Sg2MvUq6BsSmRiUD7nm+qnJiXwMMOkPeiopnAxbSMj2yTNk1SK3Qbol0ESIXZIQg1VTzzGvM59+KqW41CQyjOmWOOPqZEktTgv9qTWNwDvcKvWvd4r8tfmd3hf1BHzNs7uNQtBSVbUPWbxgSP0mcxCrFqujgluGOkcyWri6e0Y3TEgx49YU42rKk5iBd/OsozVZK96qTQLdsd4OXx7MV2xlNoLJZXVXXkoA1V1NWr6VdJSCjU0YkzZpNy6SE0a9KWrp6t4g2hf+oD0ha6aniVS5pM8cgZVJw0SQV5VXR2pLSqU2rWbTuaBDPIPc9laKUuVTVXPiRTNgl5IHM4NsJqoH5JUmGHTMbE6ez3Ak3RtKyt8qlj6+rVirG02wV5emqWcY7ROq9dF+29UvRFSuzevT9nS5NOKuRKcu1jlg6ZvvWUKhO3AuC8gm7ovKoRDaKZFd6OuqYyXau806u9GS5k4mRog9O3npRPE1W0KuVyrp2OfR37oQN3Okxzdztjeg6krGoTcW9j3iRVmjpA7dUh+kUxNBxLmmPhaqkOXKPIxZH4ScoerY64FHQdTxCnKxkwySftj4+aZJQmBy/+hh74iTwZc+5f5Xm9POlMVXdITcjT5z4/X5NXlS/1FWKX+YS2Hnc+j6DjPXHUAAGGQAAAAAAaCzrXsdWKy+TszEKcdUSJk4aDIXHbM8Xx0kMXuiF1qeANIWQta2s9baKp1DDBV6UvOJB1htmcujbSqpj997ghB3c9TnGqMwuXWjTbbMr6RqFyTHdwO2SJi3N42v8ArGXjr8KH7vK/mr+mY1Agxnuh6ytE1hqppCuqtYRT9wZq7Z4Tjo6SKunUU5dRtnXpP4gnONN5vKI+WBl5q9kVPU6atvJJDvkO2+8KcnhjoXx2rcbg2YrvjjLv5a2zZ3aSlagLLzE0+lIxBV0vKyq7rUrp29hU5yl29e4UYFm8cyD7GBpuiJmfaXKmFykZN4aVcIIpNSm7a4XSIfSUvdadXiDUGT/MjhAWGQo+OZGn64SlFWUNCI4eeEV7byqpugkU5j6jCVlorUnoXB7OTr7GdreYxKeUlj4cfF1UEuqgXiw0lEEZeLXrFathji3ynJ41nbFSNBNGTypa8qirZ4m0oZ3MuMWRTdUqWvbL32obBrijY24NIStOzKHOI2RQMgoX45O7Jvj3QFmMY6aOZm6UrPEw+eD1uVJztr5i3VSucXFU25kTQK6pjcZ1mf7lV+5pwxJ/RCWH2RA6wDvCkOEIqSNSw5NtV1FJyCpeu6bOMEiG/ssD/wBYnj9keatjpLV9D49ni1Rk5w8wcjjDzByI1kHGPmDkAHxj9YaOzi3tWsFYafqSOw5WpXOJIuDb6deKr9fjIlxF6WnaU0/X0DeP2BCHPC6xrDMhl/ofHHlI9q4f1M8Tw66CZebm8bX4w3hHeWIoLJ+HCUnmWGtUnaK3TKLVNziadG57LvzG1mcvFdpUxj9LqeANiAA9TCGkNXzmycrJ7zQNz2RdaWY8gqjo+uqvYwsiqds5bGnXSpW6/FqJpOY+rbLq8QSoy+MGi1raXnEZWZl3MtEtV3DiWk13hzHMTUfYVMYpdox9zSMXzp0J8neXKqkEk9TqOSLKIf0G0f8A6WsaHym5kFIzL/GUXDMTVBcFJ8uwiono8kbtvOHBuigTlT+IKPpVc7GueRxI6/Mcto5tVZWVkYCl6EnJ9nceVVLyLeJl3CDdBmXz1dchD6Sl7rTq7A2BZ+x7+37Zq5qKu6orGcIXWoaQmHHNCG7lDXpOXv8AUPVtJactvm72Uln3k7WkyflZeaWLtqn+1JdVIvRKNiCzGv3byUbb9YeFFhd4rYsLv2+laZf6Sc6S1NnHTbLl86VL3pvjjbORy9MleayCJajOb5NKYeK09PFPjtmdIbPKY9+TSbHutQxoYBlPdfIbnfuzSyWGhlVFPsqkKl0eVSPggc3h8qYwoc2r27uv+HvznMqk7wABx3rAAAAABxiA8qoJxhTMHJTUkuVtHxzZV05WNuppELiY5sfuFKK7stZX1zpKqb4VEjjhO1s8PzFJX9wxiZ9LdAvieFoIJG8I1Vi9IZNriOGuJiuXrdCMLp6q7hJI/uDnGHUTT6FH0dBQaBdDeOYoMi+CQhB0eFVvLZ5/8vfmuvEY/s9sYlcm3xrgQCrRGemqckCJm5s9h5FVqZMxukcpD6VfCGWgO5n4eOhKUJ7xV55Naiqmvb11LSdf1nVj1eMZuMUmRp90kTnCSpSm16VSmMJ81CePbU5IGknhmEakgYy7vnR250kik2z8qQ+ovf6hX5ctyjl84QOPn1VCM4aZcpO1Vj7BSIuSckuY3enxOf8AmwEkWpXma2ZI6XTXYWfYL60G5tRD1IqU++fqtiH6PSFCmesZQ/Z6DmVbzjb2x6NbWYtTXd36omKqXuJXUFbNV4fyDZYzTjnbtDXsG1HNsp+6N7sS+goVCnYlJggu9cpJ+qyDtV0qbvlVTGMYd1FBJsgRJBIqKSRdBSELoIQo+xYrq1x6uTfyZWS9GtMq80aweauobW8fI0dXjdWoYBv0Gr9P56QJ3xCYm+4QgDGMx701H1tY2uENhxCVuzbqHJ/wrrZcF8MpAHEvr6WZe14F+bePGWVkQAAqOkAAAAAAAAAAAAAAAAAAAAAAAAAAAADjHzAFc1kyYs745jWKnzySuHDrHV9qV2iDdQ1bcuN+VNn3mDL4clD3Og27xsbHdO/Zl5I6XfclteGNpD0HEltX0eE/KQ15Gcg8qqKojKMgnk1NPU4+MaJ8osuobjKUo5qSpIyjIF5NTLxGPjGifKLLrm0lKUaQpOnpPMnPMK0q5oowoFkry9OUyuXaeG6L10X3pf8AR7MpfpFQqq298+1DN64Yss6VO1POUurGU7UkqlKNWMoTDUZBc50yODl+t2zjV0i08Qe4TeizFhaMrZqXQszcHjVVib+121LxTFP44ljaCuUrlWwpip0jkP5IsUlVdHRV09tJ4B9ZRWo9tkoupzpeLRXbj/8AGYAAw+71fNrX2zqKp3Jik8jmZlUiH6Su4kXwz6Ci5P2YcaqG9mIYevwZCfLW2uo9J2Wr648w4Qxw3TExI3L8UTI4+wI/ZFLYuLR5WKFhpFMycw6amlX+B9/l3JzL6Td0QpyE8ASA6I8pP5fS4R1jh9AADCQAAAAAAEGs5JDRWcjL9JqYdoeR82wIf+MKkU3x8Bmo6PCRUi/PaOn7jQ7bFxK27nG84dIm+qz3HBPubRDG7khhzBTbSp4SPl41crmPfoFdIKl6SRiaiGHa4U8a6vIfmqs5nGbujW157qtqEjUIZpH/ACR1ZO6msVT6O+6P0jK9VIvSMPm816GVrmLNgzannawlT83iIBubtrlXrH6qZekYfhZ60LmkHT2rKsfFnbhTBfm6Q6DVLotW5OikX3YuTlv7IuTVVGvHi2oZ5HUHNos1NSULOItiSDhs4jynJhx9tSNgrsGNtaTEIf3IseFeGb7A9k84lHXCQJiRo95u9X0dLFI3JLk/stHjiwls5SeNUl0FSrJKlIcpydMgh43tzKtc/I48TEL8fth+wABzlIXUbcF34caOOvTDWtrUMZfhGYjBDDE5YmgF3Cx+ryjrSXD3eAn0IQcH9FHuLcK7t6VC4ni5l+lT0Cofps2nYOqXuTm0eEQ4m7xjy98trJSfRuLX4VMYvoAARLgAAA+cfMEFs0hTM8+VpXCvnT2lZFqh/KlMc5/cYidGPZxEMOEgiFaWZWsu8gmc6VD1DgnJGIXcYvNCSpvGIkXwxLVLWccq3Ij4lMosiAfCKyblAi6CpVklS6ynJuGKNa3mvW2tmkyiottjUFbzB8EYmDRx4zKH+2q9VMvFjqMPSSnrh88jTOc9Ivi91zUKVjUqZjo3GpavqJMzRhBkx4+UKcmkyqvVQLxY6jCHGQvBe1mZar6CmU0SSR2y7Tli/bUFNfEU3VMXWbwCCZNn7QqUQd7UdSPS1BX0ztSUqcuwQnQboF6KZfdiHmaBb5ROdqlq7T7SzkeavnOJOr87uMPELj4wp3bRzGyTucXMcxlxo/5wsRAfCKxVkiKpGKchi6yHJ0h9joYz6dXAzjpnoDXVlCYvuEbdqoYYaGNtjEXxL1jSBOL/ALjYoxHIFGY19cu894MccFI2UkUadhVMek2aF7YcvcnMZP8AnIYUObL+N3fw8NrczTdw8wcgA4L2QAAAAAAIm8KCxUd5NqscplxN5HvI52Yperg8SLj78fmzcpP2bdykbWkqkVUp+5MN8Xxtyld6z1Y0UriUvk3FOGSShvMSVMTHkj+CfSbwRC/KrWbiqrNRLOTIZGfp0xoGUaq7yC7btW13WnSbwh0+DL3Si85+Zr6wjLDbw/F48QYNVXLldNs3QKdVVVU2ghCF3znODx+2jWTh48XSbNECnVVVWNoIUhemc4jtg7d5t5lVJsddhZuNX0qqk1JK1IuU24XqtiG8b3nWlPX0eZqpzL3z7UZc80y8vBGxlwYqG5CiotyaGZzCuBirSZjaj4qlLj6gUxMSlN3QnjY2rUK5s9Rk42KkiR1GN9SSRdBCmKTQchO8OQwxfM9bttV+XGrYFm2TRK1jucM0kSaSEMh20hCE6O5o8Mak4Ne4BZ+0EjSyqnzVAPjHSJ/EL7Rfd8qKcf4rv/TrWyjyeFtD9cpdgADoPPtEZuUfJGHtrDJbbuWruJaIE7rlTgPbhYr5c+eGg6eQLy0LbpsrUsqboFdKl0tUu+3Ff5zgOFyLMZsy97+OqzHjRwsMAAHPdYAAAAAAAAAAAAAAAAAAAAAAAAAAAcDkcAI9ZzLBOr52tTNTyhWde0y7LM067xxxL81J+pGN1VS7PfaMeiNEWhvD8uGgnLtimlF1ew1spOHkCn1MX5dg5VSb+jX/AK1ifXFhjgIl5mcpErP1fjdK0L9CnLlpJ6XrJxhiWPqBIvqS/VV8zSf+vrluca/wpOZzeHjlQ/6Rau9lkureqWYr1DcKFLGMlSrIw7WNUK1wMXrF5Ta8IwkzTZJVGGblmjMTyBNhXyOKYiXgENtDU1JZn4ks4elbjxjm2Fct8MCqxVQdqRU7tBxumL1PjjdKKyTlIiqSpVkj7ZTkNrIYdqvNXdF5Dk45EceFZHtaMzK2SrC/lPHphvNwsNT/ADlNfAyrRVRwY5e71aSjpZdrIXCsPCkp1Sq4Sdporjlit1mipVUNe9yRtXhaTCQYxeuLm0nbOOM9qeoGUKhiXWTBwptn7wm+fwA0htuQtunX4Ece1lA0bDU8bOZf1hSzEvObTUI+LIVG/L51KPy+dMi9Ypel4fcD4hGdy86B8I+imMhb21C+y/rKSS5J9JJdIjNLqn6//wADTrtJaWmbI0JG0hSMcWOh2JdkuPZOofHeUUN0jm4uybH/APoc7k8nb2xd78d+OzTnxLGc+bgORwORynpAAAAAAAAAAHlzcMxqCGfRUi2Tdxz1E7d03WLqIqmYuk5TfdLiKzj0/UWWKul7HSVSuabp6TcmdUPVhmyTjlUDn22BuV2eVKY/+tZBaJj5g1veyyNJ3/oN3SlXx+LtgrjiZFYuGldmr0VUj9Exf/8AdkS1WeFLZWupjfHWSAUNk0cwVyka+Jcyde1UkY3zZINUHGJ8TF0nLoPju6DiSaJDEblKqbllSF2j6dGoaRnGN38o+J2VYxD66dtUMcea1hCJcq/Zo9V4h3PX930BmVC35t7clBFSnaui3yx/3IdfknBf6I2g3uB26La5drx/No5OJe/4w1feTJ2e+0sykapr2QVxZlMk1btWCCSSRTb33OhvDZFpbWzVrYhlDKVo8qOEZpck1bP2qRDJF6JeVLtaS90NjjD6xu5RVvGx1qiqmLiNHqLhyXljd6lvG8ATaQhLdT8XkXQxV0ZgNHXnqeauhVTWx9uVeWq6dL/tiQS2koWO9VVVP0THLuk7vuyD8Iiurm5oV8Yuy8A5hKZUPodXEqJA6DUpOnzRI20qb/RtO8Jf5cctNL5baWWjoXFeTnpA/OJmoZHHW9kVusc/U7JtJMPM4/rm1Gxo8nlx7a3a4H4yWJeJcze1NuIW0NvKeo2n0Obw8O1K1Qw6Rusc2PWObExzd0bEZkOByOO9WAAAAAAAMWuFQ0VcqiZ2k51HFxETDRVm4T4+zoMXEuz3XSwGUjgBV/QmNW0LKSGX+o6mXper6f24WdK2SW8mYna5IyXK7Oopd7vO4OPim8mzml7llr1vcqceVPhgbA7t+2QccoUxcSnLjrx3dGImrmVy0U/mPploi7XWg6oiTYuIOomXzywX+MTHEpdRf4PNER1bv1hl7k0aYv3BrRZcDYpMq7jETqxUj1dWkvalO59wUdWi+MvbY85zeLdVtZx/2b0IQ/JaTG1n07+kRtvHky+XpOtpWqa+k11myXJNkm7FBJJIn2CiQVPVHEVZHFkIaSaS7JXdcMVyqkN4RR6Y6kowtj7nma7buNPbGGvrUW3mraxLaKdVk8qWKaI8g2QftUiKolLucSpNo3hDYI6MxNx9PMFX0rINo1klvOHapUkieGYaWXvvUF5ZtWkrCQJqvlNXJuqpdpmSh4vDrnVP54buS+Br3RpKcKY+qavj38ufXEXbv3W0vUEjHWfoHHndwKswxQ1kw4yRjM3nrpXqbOrSJxWZtVDWUtjT1EwJdMdDNitynNhhqVPvHUN3RjmMbHvhrrK/lWisvUc/kXcipVNwZw3LzlTuy8arg32pLqJF6v8A7cC788wcK+7xZbPacTix4teuH2AAKy+AAAAAADjHixFfuZ+jH+Vy9Lm8kQzXcW2qoyTesWiBdfke83Un+BC9A3HpN3WJvrnKLAseIeZNQzGooh3GSTVF+wdpHbrtHCetNVM2GkxTFx3ijaEswltFDZVG2OslctzbBvMwUVyji6sqpSz/AOaGrCKboFamSPtE2i7Spe/GeWYtY5s9SiFN/JE5nYpmXkmabpqkkZuXWc++Xe3x5ta5Ybj5WJV7LWbbKV5bNdYy7qhHK/zbHasdR8WSpuPUTuN/v94deiM1NuqxcHj15rClp9I2leEqIvMHaCvV7bsmP3ph26La5+7Pc8jy+Nyao+Hj3RZfcekJeuIVeLjanWplu6TM3XUatklVTkNs7Jzbg0ZavI+WzdReTVKXDmI98ZPk1MDMkFElC9QxDdgwk02cpPEiKoKlWSNunIbWQefPVbB0q1O5mpqPh25d5Z86IkT3QsyhCXvllzqrboQ8KOHeYIros0knK/OXBC6FVdOjWbr6Bgd7bwsrQ0wVYiBpWpZFTFnCwiBdTh+6NslKUpdrTq06v/gMMc5lnFxJVam7JUw9ubUeGwZ03TOlFM+7XXNoL+t1xvrLbk6Voep8bk3MlyVndJwTAqTjAnzFDJdntLMmOHdb/wD24zaq1/LjHGsHT4f4yyc97e1kmS3L89shbp7IVOoV9cSrHPktUTvs48SptxuXuUim099if6wCRADhfL2OMdMdHIAAMgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAOAxw7AAAwm49qqOu1D4RFZU1GVLH4n0lSkWxVMU8cekQ2O0Q38JccMRFuruDjtvSse5lKKqWvKAJgbVgxp6oTkQ4/6Yih/dAAz1yisxjLAaIyho13Lox8pd+6pmqmPEciVRELx/8AQEhraZA7J2wkUpdCk8KknNfHjKVOuaRWxNx7+BVOMhTd0UuGIAJuuejSqMcfGEkCJlTIUpcNJcPrYD6ABAsOQAAAAAAAAAAAAAAABxxDSNy8nVlrwSbhxVFuYZ0+Phyij5mmZk5UN9k6qBiGN4WOIADGcdWrlOC3sKVcqKcVPJN8cOPkCT7rAn9WsZ9b/InYe2SqT6GtvEqvS8RiuJXXIHKbzdRcVzH04/wl4gAZ65YxjH+m/EUyIJ8kmTAhE8OIuBcPMH7AAw2AAAAAAAAAAAAAHHEPLnIdhUEQ7YSjFtJR62HJLNHaJVUli/YOU2GOGOAAAjLWHBs2Wn5hSRgWU1buSV7J3VHSh2eP8yZsDpl8EmA0QtlYOhOeRZbw3V5rxcXZqImr+vkQAT4znoqWxjnPrhuqiuDcs6Q7KaqgtR3EkDYlUIarZpV0QmPeE0FNh/AfAwlHTNMxFJQ7eIgYtnCRbYmlBlHIFQRSw7khcMC4f1AAhznKzjHR7IAAw2AAAAAAAAAAAAAAa8uLYm3d5mBPk2ouFqQ/J8RVnzQp1k8O4V4tZPBNgAANFvuC6y/uXah2NPy8IXHzU46cdFL/AFHOYexSvBs5eqTeEdfIGSbc/bJt84eYeIc+j3IAM9ctdcdfhIWl6biKViEIyDimUJHIl4kmcc3KgiTD+AhcMMMP6h7PEADDOHIAAMv/2Q==" alt="" width="300" />
如图,这里以N对N为例,X为输入,y为输出,h为隐藏状态。
假设输入X_t对应权重矩阵为U,隐藏状态h_t-1对应的的权重为W,输出y_t对应的权重为V,这里U,W,V一般对各个时刻t来说是共享的。
对于t时刻,有以下公式:

其中第一个激活函数一般为tanh或relu等,第二个一般为softmax。第一式以矩阵方式运行,提高效率。
TensorFlow调用:
tf.nn.rnn_cell.BasicRNNCell(
num_units,
activation=None,# type string
reuse=None,
name=None,
dtype=None,
**kwargs,
)
BPTT(back-propagation through time):反向传播
t时刻的损失为:

求和,求偏导:


如果我们以tanh作为激活函数,则中间项
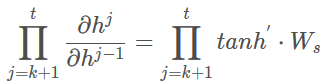
由于tanh函数偏导小于1,多次连乘导致“梯度消失”,如果采用relu激活,导数为1容易导致“梯度爆炸”。
解决梯度爆炸:通过梯度裁剪,容易处理
解决梯度消失:下面将要介绍的LSTM
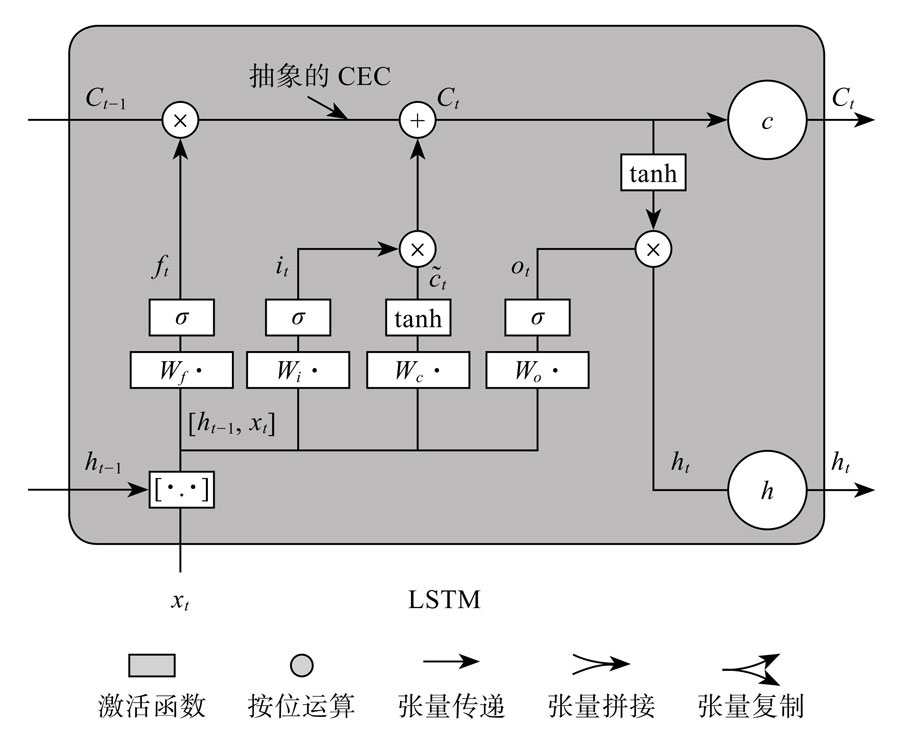
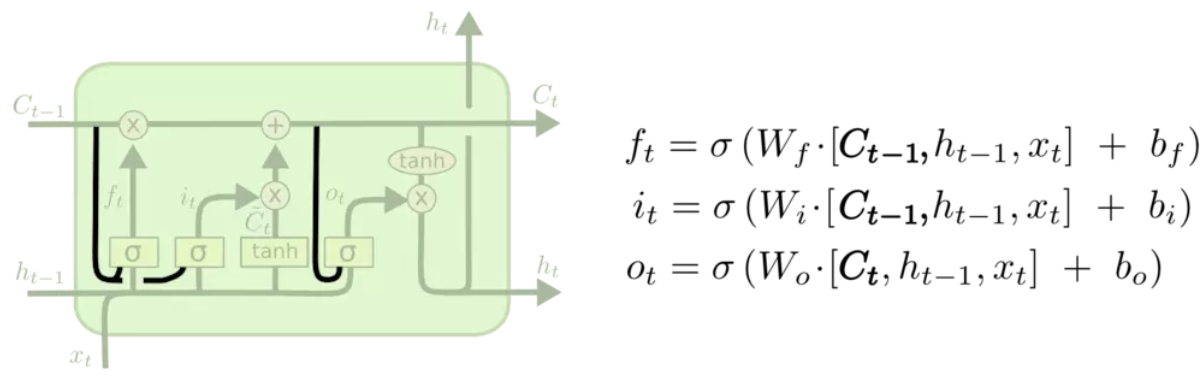
2,LSTM(长短期记忆)
LSTM通过门的操作来实现信息的选取,遗忘门通过一个sigmoid激活函数对上一个细胞状态c_t-1进行更新,再加上输入门的新信息。
可以看到,上面水平线中,只有与门的2个交换操作,以及一个CEC(常量误差传播子,权值为1的自连接,一个线性激活,保证误差传递而不会发生梯度消失或爆炸)。
相关公式为:
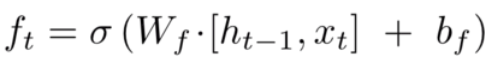
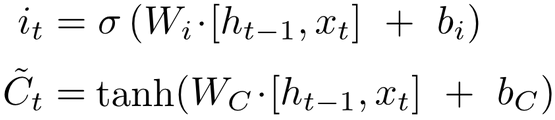


TensorFlow实现:
tf.nn.rnn_cell.BasicLSTMCell(
num_units,
forget_bias=1.0,#Ger et al等在2000年提出,遗忘门偏置为1使得LSTM更加健壮。
state_is_tuple=True,
activation=None,
reuse=None,
name=None,
dtype=None,
**kwargs,
)
3,LSTM变体
- 变体1:添加图中深色部分连接。个人理解:输入和遗忘部分加入之前的细胞状态学习可以获得更多context信息,输出门添加基于新的细胞状态信息学习。感觉上比基础LSTM要厉害些,也没增加参数。
- 变体2:输入i_t直接用1-f_t表示。个人认为这样做不太恰当,需要遗忘的细胞状态信息,以及需要增加的输入信息,它们应该分开学习。共同学习存在一种矛盾:比如遗忘的部分想要降低参数,而增加的部分想要提高参数。好处是参数减少了。

- 变体3:GRU。使用2个门(重置门和更新门)代替LSTM的3个门,计算效率高,内存占用少,效果差不多,实际中比较流行。将细胞状态c与隐藏状态h合并,这个变体思想类似变体1,参数减少了不少。
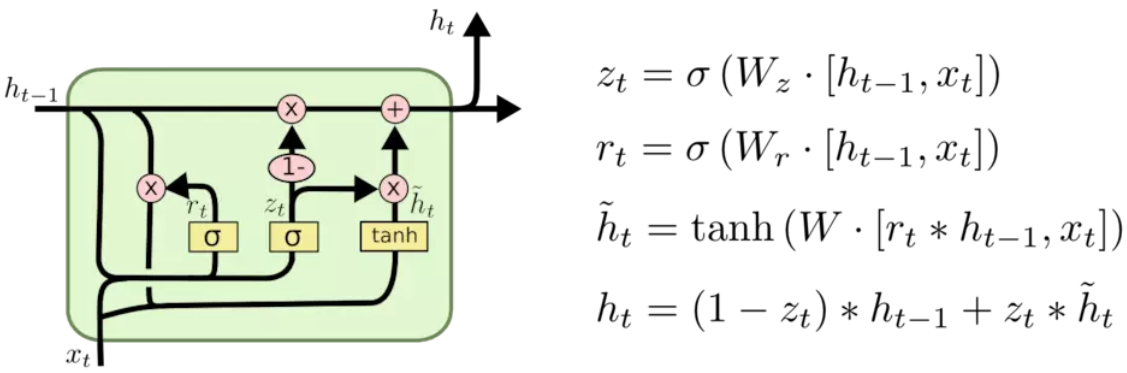
TensorFlow GRU实现
tf.nn.rnn_cell.GRUCell(
num_units,
activation=None,
reuse=None,
kernel_initializer=None,
bias_initializer=None,
name=None,
dtype=None,
**kwargs,
)
参考资料
https://blog.csdn.net/zhaojc1995/article/details/80572098
《python深度学习》
RNN汇总的更多相关文章
- 【RNN】资源汇总
wesome Recurrent Neural Networks A curated list of resources dedicated to recurrent neural networks ...
- 机器学习&深度学习经典资料汇总,data.gov.uk大量公开数据
<Brief History of Machine Learning> 介绍:这是一篇介绍机器学习历史的文章,介绍很全面,从感知机.神经网络.决策树.SVM.Adaboost到随机森林.D ...
- 『TensorFlow』专题汇总
TensorFlow:官方文档 TensorFlow:项目地址 本篇列出文章对于全零新手不太合适,可以尝试TensorFlow入门系列博客,搭配其他资料进行学习. Keras使用tf.Session训 ...
- (zhuan) 深度学习全网最全学习资料汇总之模型介绍篇
This blog from : http://weibo.com/ttarticle/p/show?id=2309351000224077630868614681&u=5070353058& ...
- 时间序列(六): 炙手可热的RNN: LSTM
目录 炙手可热的LSTM 引言 RNN的问题 恐怖的指数函数 梯度消失* 解决方案 LSTM 设计初衷 LSTM原理 门限控制* LSTM 的 BPTT 参考文献: 炙手可热的LSTM 引言 上一讲说 ...
- Big Spatio temporal Data(R-tree Index and NN & RNN & Skyline)
一.简单介绍大数据技术产物 “大数据”一词首先出现在2008年9月<Nature>杂志发表的一篇名为“Big Data: Wikiomics”的文章上(Mitch,2008).“大数据科学 ...
- 机器学习(Machine Learning)&深度学习(Deep Learning)资料汇总 (上)
转载:http://dataunion.org/8463.html?utm_source=tuicool&utm_medium=referral <Brief History of Ma ...
- (数据科学学习手札39)RNN与LSTM基础内容详解
一.简介 循环神经网络(recurrent neural network,RNN),是一类专门用于处理序列数据(时间序列.文本语句.语音等)的神经网络,尤其是可以处理可变长度的序列:在与传统的时间序列 ...
- 普通神经网络和RNN简单demo (一)
2017-08-04 花了两天时间看了下神经网络的一点基础知识,包括单层的感知机模型,普通的没有记忆功能的多层神经网咯,还有递归神经网络RNN.这里主要是参考了一个博客,实现了几个简单的代码,这里把源 ...
随机推荐
- 前端知识体系:JavaScript基础-原型和原型链-实现继承的几种方式以及他们的优缺点
实现继承的几种方式以及他们的优缺点(参考文档1.参考文档2.参考文档3) 要搞懂JS继承,我们首先要理解原型链:每一个实例对象都有一个__proto__属性(隐式原型),在js内部用来查找原型链:每一 ...
- docker学习系列-jdk基础镜像制作
准备一台安装有docker服务的机器 1.编辑Dockerfile vim Dockerfile FROM centos:latest ADD ./jdk-8u141-linux-x64.tar. ...
- HDU 6074 - Phone Call | 2017 Multi-University Training Contest 4
看标程的代码这么短,看我的.... 难道是静态LCA模板太长了? /* HDU 6074 - Phone Call [ LCA,并查集 ] | 2017 Multi-University Traini ...
- Linux 防火墙遇到的问题
一直报这个错误,写个博客来记录一下问题 在centos7中执行service iptables start 报如下错误 执行如下命令 systemctl stop firewalld systemct ...
- Java进阶知识12 Hibernate多对多双向关联(Annotation+XML实现)
1.Annotation 注解版 1.1.应用场景(Student-Teacher):当学生知道有哪些老师教,老师也知道自己教哪些学生时,可用双向关联 1.2.创建Teacher类和Student类 ...
- [Luogu] Mayan游戏
https://www.luogu.org/problemnew/show/P1312 太恶心了 #include <cstdio> #include <algorithm> ...
- 【CUDA 基础】6.3 重叠内和执行和数据传输
title: [CUDA 基础]6.3 重叠内和执行和数据传输 categories: - CUDA - Freshman tags: - 深度优先 - 广度优先 toc: true date: 20 ...
- tensorflow实现siamese网络 (附代码)
转载自:https://blog.csdn.net/qq1483661204/article/details/79039702 Learning a Similarity Metric Discrim ...
- NSObject和反射
如何NSObject和反射 NSObject 常用方法 如何判断 某个对象是否属于某个类或子类 -(BOOL)isKindOfClass:(Class)aClass 判断是否为aClass的实例(不包 ...
- python性能测试值timeit的使用示例
from timeit import Timer def t1(): li = [] for i in range(10000): li.append(i) def t2(): li = [] for ...
