RMQ((Range Minimum/Maximum Query))ST算法

给定一个数组，求出给定区间[l,r]中元素的最大值或最小值或者最值的索引。

一看到这个题目，简单，看我暴力出奇迹。暴力当然是可行的。但是时间复杂度很高(O(n^2))。线段树，树状数组也可以解决这个问题，复杂度(O(nlogn))的预处理,最终查询为O(次数*logn)。

而今天用ST(Sparse_Table)算法，也是O(nlogn)的预处理，但是是单次查询为O(1)，挺高效的。

我们现在给定一组数据 n==9,元素为2,4,6,8,9,1,2,3,4。一个二维数组f[MAX][MAX];假设我们求区间最大值的问题。

f[i][j]的定义是这样的，维护从当前i的位置开始，共2^j个元素中的最大值。

如果f[i][0]则表示从自身到自身(2^0==1)的元素的最大值。f[i][1]表示从自身到下一个元素(2^1==2)中最大的那个。依次类推。

但是，这个二维数组也是有范围的。总共就n个元素，所以j的最大值为log2(n),而i的范围则是受j的范围影响的。即j每次跨度越小，i的范围就越大，如果j的跨度较大，i的范围就小。

另外，f数组的计算过程如下

f[1][0]就是数组本身，f[1][1]就是自己和下一个元素的最大值，f[1][2]是自己和后三个元素中的最大值(共2^2==4个)，而这个不需要重新去比较4个，而是在f[1][1](有前两个和后两个的最大值)的基础上，比较2个就好了。

这样，每一个元素往后的2^k次方的中的最大值就保存下来了。

那么，如何计算给定区间[i,j]中的最大值呢

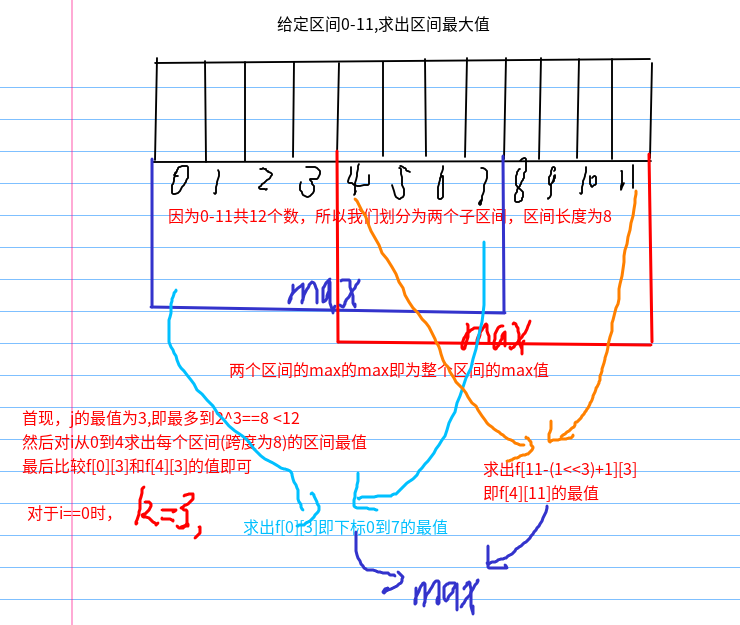
上图中1和11表示查询区间端点值对应整个查询区间的范围(i,j)，根据范围分别算出两个子区间的f[i][j]中的i(起始位置)和j(跨度)，即f[i][k]和f[j-(1<<k)+1][k]，子区间范围是2^k==8，求出二区间最值就ok。

那么，两个子区间的范围k怎么确定呢？很简单，根据要查询区间i到j(0-11)的范围，那么k<=log2(j-i+1)，即不超过要求范围[i,j]的2^k的最大的那个k。这样，无论如何，两个子区间都能完全覆盖整个所求区间，重叠了也不会影响结果。

图中找出2^3==8< 12,子区间是重叠的，如果[i,j]是4,那么2,2的子区间就行，这个则不重叠。

这样，就能得到问题的解。这个查询时间复杂度是O(1)的，上述计算在预处理中即可完成。

 　　 for(int i = ;i <= n; i++)//预处理
     {
         f[i][] = arr[i];//从i开始，长度为2^0距离的最大值为自己
         v[i][] = arr[i];//记录最小值
     }
     //int m = log2(n);//st
     for(int j = ; (<<j)<=n ;j++)//2 ^ j <=n ：j <=m ，找出每一个不超多范围的跨度的指数 j
     {
         //int t = n -(1<<j)  + 1;
         for(int i = ;i+(<<j)- <=n ;i++)//当前i加上区间范围不能越界，到后面j越大，i的范围就越小
         {//更新最值操作
             v[i][j] = min( v[i][j-] , v[i+(<<(j-))][j-]);
             f[i][j] = max( f[i][j-] , f[i+(<<(j-))][j-]);
         }
     }

这里的更新最值是这样的

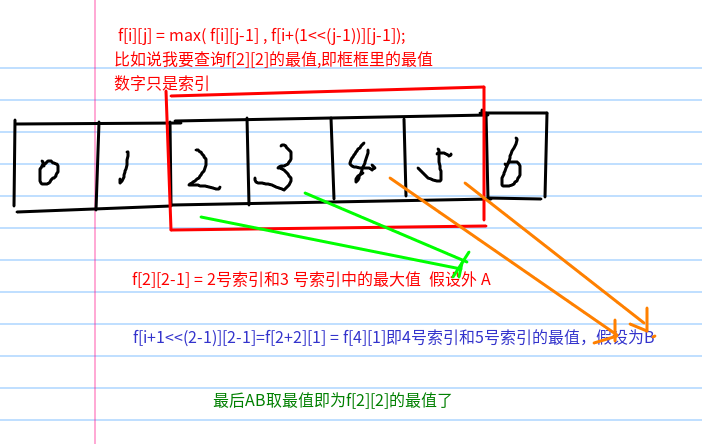
那么公式怎么来的？？？

针对j的跨度变化，比较的元素也会不同，请仔细研究第一张图片

最大值查询

 int st_max(int a,int b)
 {
     int k=(int)(log(b-a+1.0)/log(2.0));//计算出最大跨度
     return max(f[a][k],f[b-(<<k)+][k]);//找出二者间最值
 } 

这个题目可以练练手，纯RMQ(线段树当然也ok)---- 传送门