JavaScript数字精度丢失的一些问题

本文分为三个部分

1. JS 数字精度丢失的一些典型问题
2. JS 数字精度丢失的原因
3. 解决方案（一个对象+一个函数）

一、JS数字精度丢失的一些典型问题

1. 两个简单的浮点数相加

1	0.1 + 0.2 != 0.3 // true

Firebug

这真不是 Firebug 的问题，可以用alert试试 （哈哈开玩笑）。

看看Java的运算结果

再看看Python

2. 大整数运算

1	9999999999999999 == 10000000000000001 // ？

Firebug

16位和17位数竟然相等，没天理啊。

又如

1 2	var x = 9007199254740992 x + 1 == x // ？

看结果

三观又被颠覆了。

3. toFixed 不会四舍五入（Chrome）

1	1.335.toFixed(2) // 1.33

Firebug

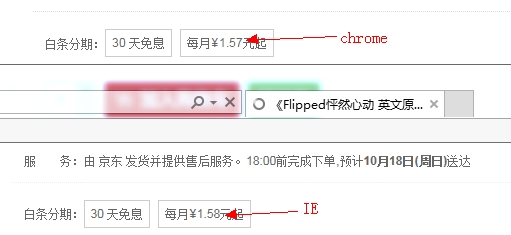
线上曾经发生过 Chrome 中价格和其它浏览器不一致，正是因为 toFixed 兼容性问题导致

二、JS 数字丢失精度的原因

计算机的二进制实现和位数限制有些数无法有限表示。就像一些无理数不能有限表示，如 圆周率 3.1415926...，1.3333... 等。JS 遵循 IEEE 754 规范，采用双精度存储（double precision），占用 64 bit。如图

意义

• 1位用来表示符号位
• 11位用来表示指数
• 52位表示尾数

浮点数，比如

1 2	0.1 >> 0.0001 1001 1001 1001…（1001无限循环） 0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

此时只能模仿十进制进行四舍五入了，但是二进制只有 0 和 1 两个，于是变为 0 舍 1 入。这即是计算机中部分浮点数运算时出现误差，丢失精度的根本原因。

大整数的精度丢失和浮点数本质上是一样的，尾数位最大是 52 位，因此 JS 中能精准表示的最大整数是 Math.pow(2, 53)，十进制即 9007199254740992。

大于 9007199254740992 的可能会丢失精度

1 2 3

9007199254740992     >> 10000000000000...000 // 共计 53 个 0 9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0 9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

实际上

1 2 3 4

9007199254740992 + 1 // 丢失 9007199254740992 + 2 // 未丢失 9007199254740992 + 3 // 丢失 9007199254740992 + 4 // 未丢失

结果如图

以上，可以知道看似有穷的数字, 在计算机的二进制表示里却是无穷的，由于存储位数限制因此存在“舍去”，精度丢失就发生了。

想了解更深入的分析可以看这篇论文：What Every Computer Scientist Should Know About Floating-Point Arithmetic

三、解决方案

对于整数，前端出现问题的几率可能比较低，毕竟很少有业务需要需要用到超大整数，只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。

对于小数，前端出现问题的几率还是很多的，尤其在一些电商网站涉及到金额等数据。解决方式：把小数放到位整数（乘倍数），再缩小回原来倍数（除倍数）

1 2	// 0.1 + 0.2 (0.1*10 + 0.2*10) / 10 == 0.3 // true

　　

以下是我写了一个对象，对小数的加减乘除运算丢失精度做了屏蔽。当然转换后的整数依然不能超过 9007199254740992。

+

toFixed的修复如下

+

相关：

http://0.30000000000000004.com

http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html

本文转载自：https://www.cnblogs.com/snandy/p/4943138.html