BZOJ3153 : Sone1

Top Tree模板题，写起来真不是一般的蛋疼，调了两天。常数写渣了TAT

Top Tree就是在LCT的基础上加以改动，将虚边也用splay维护，

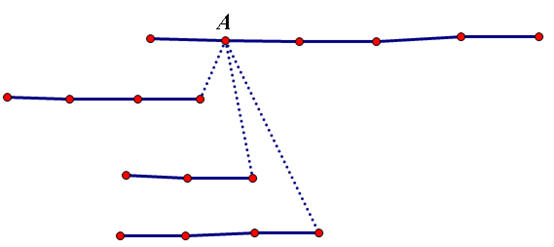
对于A向儿子所连出去的虚边，用Splay维护↓

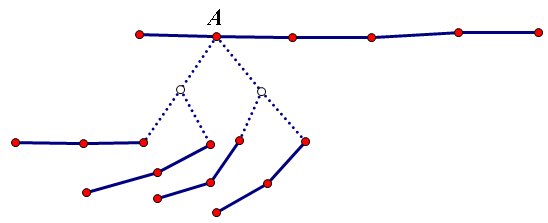
为了保证所有虚儿子不存在父子关系，需要让它们都是叶子节点，所以需要引入白色的内部点来维持这个结构。

就能支持子树操作了。

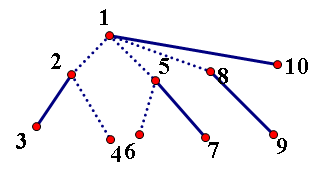
对于这样一棵以1为根的树。

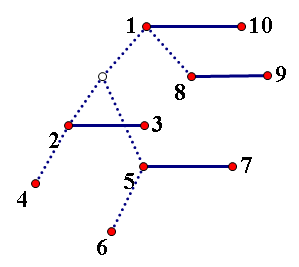
在Top Tree中是这样维护的。

实现起来就是把原来son[2]扩充到son[4]

son[0]和son[1]仍然对应实链splay的两个儿子

son[2]和son[3]对应虚边splay的两个儿子

Add操作：

Add(x,y)操作就是从x点连一条虚边到y，使得x是y的父亲。

这就等价于在x的虚边splay中插入y这个叶子节点，必要的话要新建内部点。

Del操作：

Del(x)操作就是把x点和它父亲之间连着的虚边断开。

这就等价于在x的父亲的虚边splay中删除x这个叶子节点，必要的话要删除某些已经没用的内部点。

Access操作：

Access(x)操作就是把x到根路径上的所有边都变成实边，并把x向它所有儿子的边都变成虚边。

考虑普通Link-Cut Tree的Access过程：

void access(int x){
  for(int y=0;x;y=x,x=f[x]){
    splay(x);
    son[x][1]=y;
    up(x);
  }
}

每一步都是实边虚边的转化，有了Add和Del操作，可以很自然的改写成：

void access(int x){
  for(int y=0;x;y=x,x=fa(x)){
    splay(x);
    del(y);
    add(x,son[x][1]);
    setson(x,1,y);
    up(x);
  }
}

Makeroot操作：

与Link-Cut Tree一致，注意翻转只交换son[0]和son[1]。

Link操作：

考虑普通Link-Cut Tree的Link过程：

void link(int x,int y){
  makeroot(x);
  f[x]=y;
  access(x);
}

可以很自然的改写成：

void link(int x,int y){
  makeroot(x);
  add(y,x);
  access(x);
}

Cut操作：

与Link-Cut Tree一致。

链操作：

与Link-Cut Tree一致。

子树操作：

方便起见首先Access(x)，这样x向它的孩子连着的肯定都是虚边，x的子树部分就是x的虚边Splay。

void changetree(int x,tag p){
  access(x);
  splay(x);
  val[x]=atag(val[x],p);
  for(int i=2;i<4;i++)if(son[x][i])tagtree(son[x][i],p,1);
  up(x);
  splay(x);
}
data asktree(int x){
  access(x);
  splay(x);
  data t=data(val[x]);
  for(int i=2;i<4;i++)if(son[x][i])t=t+asum[son[x][i]];
  return t;
}

信息的和：

对于每个节点x，需要维护一些域：

in：这个点是否是内部点

val：这个点的点权

csum：链上信息和

tsum：子树信息和(不包括链上)

asum：所有信息和

csum[x]=val[x]+csum[son[x][0]]+csum[son[x][1]]

tsum[x]=tsum[son[x][0]]+tsum[son[x][1]]+asum[son[x][2]]+asum[son[x][3]]

asum[x]=csum[x]+tsum[x]

标记：

对于每个节点x，需要维护一些标记：

rev：链翻转标记

ctag：链修改标记

ttag：子树修改标记(不包括链上)

rev和ctag下传方法与Link-Cut Tree一致，

ttag下传方法为：

如果是在实链中的下传，直接下传到ttag，无需修改。

如果是虚边splay中下传到内部点，下传到ttag并修改。

如果是虚边splay中下传到外部点，下传到ttag和ctag并修改。

垃圾回收：

由于add操作会新增大量内部白点，但是内部白点最多同时只有$O(n)$个，所以需要垃圾回收。

效率：

时间复杂度为$O(\log n)$每次操作，但是常数为97，非常大。

#include<cstdio>
#define N 200010
const int inf=~0U>>1;
inline void swap(int&a,int&b){int c=a;a=b;b=c;}
inline int max(int a,int b){return a>b?a:b;}
inline int min(int a,int b){return a<b?a:b;}
inline void read(int&a){
  char c;bool f=0;a=0;
  while(!((((c=getchar())>='0')&&(c<='9'))||(c=='-')));
  if(c!='-')a=c-'0';else f=1;
  while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';
  if(f)a=-a;
}
struct tag{
int a,b;//ax+b
tag(){a=1,b=0;}
tag(int x,int y){a=x,b=y;}
inline bool ex(){return a!=1||b;}
inline tag operator+(const tag&x){return tag(a*x.a,b*x.a+x.b);}
};
inline int atag(int x,tag y){return x*y.a+y.b;}
struct data{
int sum,minv,maxv,size;
data(){sum=size=0,minv=inf,maxv=-inf;}
data(int x){sum=minv=maxv=x,size=1;}
data(int a,int b,int c,int d){sum=a,minv=b,maxv=c,size=d;}
inline data operator+(const data&x){return data(sum+x.sum,min(minv,x.minv),max(maxv,x.maxv),size+x.size);}
};
inline data operator+(const data&a,const tag&b){return a.size?data(a.sum*b.a+a.size*b.b,atag(a.minv,b),atag(a.maxv,b),a.size):a;}
//son:0-1：重链儿子，2-3：AAA树儿子
int f[N],son[N][4],a[N],tot,rt,rub,ru[N];bool rev[N],in[N];
int val[N];
data csum[N],tsum[N],asum[N];
tag ctag[N],ttag[N];
inline bool isroot(int x,int t){
  if(t)return !f[x]||!in[f[x]]||!in[x];
  return !f[x]||(son[f[x]][0]!=x&&son[f[x]][1]!=x)||in[f[x]]||in[x];
}
inline void rev1(int x){
  if(!x)return;
  swap(son[x][0],son[x][1]);rev[x]^=1;
}
inline void tagchain(int x,tag p){
  if(!x)return;
  csum[x]=csum[x]+p;
  asum[x]=csum[x]+tsum[x];
  val[x]=atag(val[x],p);
  ctag[x]=ctag[x]+p;
}
inline void tagtree(int x,tag p,bool t){
  if(!x)return;
  tsum[x]=tsum[x]+p;
  ttag[x]=ttag[x]+p;
  if(!in[x]&&t)tagchain(x,p);else asum[x]=csum[x]+tsum[x];
}
inline void pb(int x){
  if(!x)return;
  if(rev[x])rev1(son[x][0]),rev1(son[x][1]),rev[x]=0;
  if(!in[x]&&ctag[x].ex())tagchain(son[x][0],ctag[x]),tagchain(son[x][1],ctag[x]),ctag[x]=tag();
  if(ttag[x].ex()){
    tagtree(son[x][0],ttag[x],0),tagtree(son[x][1],ttag[x],0);
    tagtree(son[x][2],ttag[x],1),tagtree(son[x][3],ttag[x],1);
    ttag[x]=tag();
  }
}
inline void up(int x){
  tsum[x]=data();
  for(int i=0;i<2;i++)if(son[x][i])tsum[x]=tsum[x]+tsum[son[x][i]];
  for(int i=2;i<4;i++)if(son[x][i])tsum[x]=tsum[x]+asum[son[x][i]];
  if(in[x]){
    csum[x]=data();
    asum[x]=tsum[x];
  }else{
    csum[x]=data(val[x]);
    for(int i=0;i<2;i++)if(son[x][i])csum[x]=csum[x]+csum[son[x][i]];
    asum[x]=csum[x]+tsum[x];
  }
}
inline int child(int x,int t){pb(son[x][t]);return son[x][t];}
inline void rotate(int x,int t){
  int y=f[x],w=(son[y][t+1]==x)+t;
  son[y][w]=son[x][w^1];
  if(son[x][w^1])f[son[x][w^1]]=y;
  if(f[y])for(int z=f[y],i=0;i<4;i++)if(son[z][i]==y)son[z][i]=x;
  f[x]=f[y];f[y]=x;son[x][w^1]=y;up(y);
}
inline void splay(int x,int t=0){
  int s=1,i=x,y;a[1]=i;
  while(!isroot(i,t))a[++s]=i=f[i];
  while(s)pb(a[s--]);
  while(!isroot(x,t)){
    y=f[x];
    if(!isroot(y,t)){if((son[f[y]][t]==y)^(son[y][t]==x))rotate(x,t);else rotate(y,t);}
    rotate(x,t);
  }
  up(x);
}
inline int newnode(){
  int x=rub?ru[rub--]:++tot;
  son[x][2]=son[x][3]=0;in[x]=1;
  return x;
}
inline void setson(int x,int t,int y){son[x][t]=y;f[y]=x;}
inline int pos(int x){for(int i=0;i<4;i++)if(son[f[x]][i]==x)return i;return 4;}
inline void add(int x,int y){//从x连出一条虚边到y
  if(!y)return;
  pb(x);
  for(int i=2;i<4;i++)if(!son[x][i]){
    setson(x,i,y);
    return;
  }
  while(son[x][2]&&in[son[x][2]])x=child(x,2);
  int z=newnode();
  setson(z,2,son[x][2]);
  setson(z,3,y);
  setson(x,2,z);
  splay(z,2);
}
inline void del(int x){//将x与其虚边上的父亲断开
  if(!x)return;
  splay(x);
  if(!f[x])return;
  int y=f[x];
  if(in[y]){
    int s=1,i=y,z=f[y];a[1]=i;
    while(!isroot(i,2))a[++s]=i=f[i];
    while(s)pb(a[s--]);
    if(z){
      setson(z,pos(y),child(y,pos(x)^1));
      splay(z,2);
    }
    ru[++rub]=y;
  }else{
    son[y][pos(x)]=0;
    splay(y);
  }
  f[x]=0;
}
inline int fa(int x){//x通过虚边的父亲
  splay(x);
  if(!f[x])return 0;
  if(!in[f[x]])return f[x];
  int t=f[x];
  splay(t,2);
  return f[t];
}
inline int access(int x){
  int y=0;
  for(;x;y=x,x=fa(x)){
    splay(x);
    del(y);
    add(x,son[x][1]);
    setson(x,1,y);
    up(x);
  }
  return y;
}
inline int lca(int x,int y){
  access(x);
  return access(y);
}
inline int root(int x){
  access(x);
  splay(x);
  while(son[x][0])x=son[x][0];
  return x;
}
inline void makeroot(int x){
  access(x);
  splay(x);
  rev1(x);
}
inline void link(int x,int y){
  makeroot(x);
  add(y,x);
  access(x);
}
inline void cut(int x){
  access(x);
  splay(x);
  f[son[x][0]]=0;
  son[x][0]=0;
  up(x);
}
inline void changechain(int x,int y,tag p){
  makeroot(x);
  access(y);
  splay(y);
  tagchain(y,p);
}
inline data askchain(int x,int y){
  makeroot(x);
  access(y);
  splay(y);
  return csum[y];
}
inline void changetree(int x,tag p){
  access(x);
  splay(x);
  val[x]=atag(val[x],p);
  for(int i=2;i<4;i++)if(son[x][i])tagtree(son[x][i],p,1);
  up(x);
  splay(x);
}
inline data asktree(int x){
  access(x);
  splay(x);
  data t=data(val[x]);
  for(int i=2;i<4;i++)if(son[x][i])t=t+asum[son[x][i]];
  return t;
}
int n,m,x,y,z,k,i,ed[N][2];
int main(){
  read(n);read(m);
  tot=n;
  for(i=1;i<n;i++)read(ed[i][0]),read(ed[i][1]);
  for(i=1;i<=n;i++)read(val[i]),up(i);
  for(i=1;i<n;i++)link(ed[i][0],ed[i][1]);
  read(rt);
  makeroot(rt);
  while(m--){
    read(k);
    if(k==1){//换根
      read(rt);
      makeroot(rt);
    }
    if(k==9){//x的父亲变成y
      read(x),read(y);
      if(lca(x,y)==x)continue;
      cut(x);
      link(y,x);
      makeroot(rt);
    }
    if(k==0){//子树赋值
      read(x),read(y);
      changetree(x,tag(0,y));
    }
    if(k==5){//子树加
      read(x),read(y);
      changetree(x,tag(1,y));
    }
    if(k==3){//子树最小值
      read(x);
      printf("%d\n",asktree(x).minv);
    }
    if(k==4){//子树最大值
      read(x);
      printf("%d\n",asktree(x).maxv);
    }
    if(k==11){//子树和
      read(x);
      printf("%d\n",asktree(x).sum);
    }
    if(k==2){//链赋值
      read(x),read(y),read(z);
      changechain(x,y,tag(0,z));
      makeroot(rt);
    }
    if(k==6){//链加
      read(x),read(y),read(z);
      changechain(x,y,tag(1,z));
      makeroot(rt);
    }
    if(k==7){//链最小值
      read(x),read(y);
      printf("%d\n",askchain(x,y).minv);
      makeroot(rt);
    }
    if(k==8){//链最大值
      read(x),read(y);
      printf("%d\n",askchain(x,y).maxv);
      makeroot(rt);
    }
    if(k==10){//链和
      read(x),read(y);
      printf("%d\n",askchain(x,y).sum);
      makeroot(rt);
    }
  }
  return 0;
}