线性回归 Linear regression(2)线性回归梯度下降中学习率的讨论

这篇博客针对的AndrewNg在公开课中未讲到的，线性回归梯度下降的学习率进行讨论，并且结合例子讨论梯度下降初值的问题。

线性回归梯度下降中的学习率

上一篇博客中我们推导了线性回归，并且用梯度下降来求解线性回归中的参数。但是我们并没有考虑到学习率的问题。

我们还是沿用之前对于线性回归形象的理解：你站在山顶，环顾四周，寻找一个下山最快的方向走一小步，然后再次环顾四周寻找一个下山最快的方向走一小步，在多次迭代之后就会走到最低点。那么在这个理解中，学习率其实是什么呢？学习率就是你走的步子有多长。

所以太大的学习率可能会导致你一步跨的太大，直接跨过了我们想要的最小均值；太小的学习率又会造成你跨的步子太小，可能你走了好多步，其实离你目标点还有很大的距离。

学习率的调整是我们梯度下降算法的关键。

笔者在神经网络的相关书籍里看到，1996年Hayjin证明，只要学习率α满足下式，LMS算法就会收敛。（P.S.笔者暂时还没有阅读相关的论文所以只能暂时给出结论）

，其中是输入向量x(n)组成的自相关矩阵R的最大特征值。由于常常不可知，因此往往使用自相关矩阵R的迹（trace）表示。

，所以，且tr(R)为各输入向量的均方值之和。

我们现在至少得到了学习率α的最大值，这个值能保证梯度下降收敛。

下面我自己写了一段程序分别用批量梯度下降，随机梯度下降对于学习率，梯度下降的初值进行了测试。

我利用了Mathematical Algorithms for Linear Regression, Academic Press, 1991, page 304,ISBN 0-12-656460-4.中的一组数据。

这组数据包括了30不同年龄的人的收缩压，每组数据包括4行

I,  the index;
A0, 1,
A1, the age;
B,  the systolic blood pressure.

其中x表示年龄，y表示对应的收缩压。

同时我们求得学习率  

接下来我会对三种方法拟合出来的结果进行展示，其中：

红色的线表示批量梯度下降结果

绿色的线表示随机梯度下降结果

蓝色的线表示直接计算参数的结果

第一组测试数据是在初始值  学习率 的情况下，迭代10000次得到

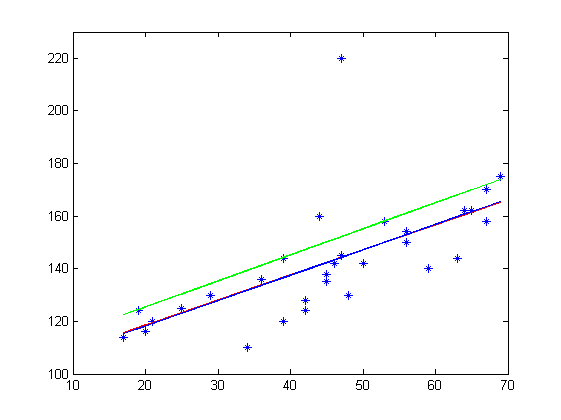
可以看出批量梯度下降，与直接得到参数基本吻合，可见批量梯度下降基本成功收敛到了mse的最小值，然而随机梯度下降的结果却不佳。

第二组测试数据是在初始值  学习率 的情况下，迭代10000次得到

可以看出此时批量梯度下降还未完全收敛，随机梯度下降基本完全收敛，而且与第一组测试数据得到的值差不多。

第二组测试数据是在初始值  学习率 的情况下，迭代10000次得到

这组测试数据由于学习率过大，θ不再收敛，而变得非常大了。

由此我们可以看到批量梯度下降与随机梯度下降优缺点。

批量梯度下降，优点：得到的参数非常准确，不太容易陷入局部最小值；

缺点：收敛速度慢

随机梯度下降，优点：收敛速度快

缺点：得到的参数不是非常准确，容易陷入局部最小值。

附代码（写matlab比较少，最后基本强行写成了c。。。）

%data
x(:,1)=1;
x(:,2)=a(:,1);
y=a(:,2);
b=figure;
set(b,'name','样本图像');
plot(x(:,2),y,'*');
axis([10,70,100,230]);
%求各输入向量的均方值之和。
mm=0;
for i=1:30
    mm=x(i,1)^2+x(i,2)^2;
end
mm=2/(mm);
%批量梯度下降
mse=100;
m=0.1;
theta=[100,1];
alpha=0.0001;
times=0;
while  mse>m && times<10000
   times=times+1;
   tot1=0;
   tot2=0;
   mse=0;
   for i=1:30
       tot1=tot1+(y(i)-(theta(1)*x(i,1)+theta(2)*x(i,2)))*x(i,1);
       tot2=tot2+(y(i)-(theta(1)*x(i,1)+theta(2)*x(i,2)))*x(i,2);
       mse=mse+(y(i)-(theta(1)*x(i,1)+theta(2)*x(i,2)))^2/2;
   end
   theta(1)=theta(1)+alpha*tot1/30*2;
   theta(2)=theta(2)+alpha*tot2/30*2;
   mse=mse/30;
end
hold on;
y=theta(1)+theta(2)*x;
plot(x,y,'Color',[1,0,0]);
%随机梯度下降
x(:,1)=1;
x(:,2)=a(:,1);
y=a(:,2);
mse=100;
m=0.1;
theta=[100,1];
alpha=0.0001;
times=0;
while  mse>m && times<10000
   times=times+1;
   tot1=0;
   tot2=0;
   mse=0;
   for i=1:30
       tot1=0;
       tot2=0;
       tot1=tot1+(y(i)-(theta(1)*x(i,1)+theta(2)*x(i,2)))*x(i,1);
       tot2=tot2+(y(i)-(theta(1)*x(i,1)+theta(2)*x(i,2)))*x(i,2);
       theta(1)=theta(1)+alpha*tot1*2;
       theta(2)=theta(2)+alpha*tot2*2;
   end
   for i=1:30
       mse=mse+(y(i)-(theta(1)*x(i,1)+theta(2)*x(i,2)))^2/2;
   end
   mse=mse/30;
end
hold on;
y=theta(1)+theta(2)*x;
plot(x,y,'Color',[0,1,0]);
%公式法求theta
%data
x(:,1)=1;
x(:,2)=a(:,1);
y=a(:,2);
theta0=inv(x'*x)*x'*y;
hold on;
y=theta0(1)+theta0(2)*x;
plot(x,y,'Color',[0,0,1]);