java垃圾回收机制--可达性算法

　　

　　先说一些题外话，Java虚拟机在执行Java程序的过程中会把它所管理的内存划分为若干个不同的数据区，这些区分为线程私有区和线程共享区

　　1、线程私有区

　　　 a、程序计数器

　　　　记录正在执行的虚拟机字节码指令地址。此区域是是唯一一个在java虚拟机规范中没有规定任何OutOfMemoryError情况的区域。

　　　b、Java虚拟机栈

　　　　描述的是Java方法执行的内存模型，每个方法在执行的同时会创建一个栈帧

　　　c、本地方法栈

　　　　它与虚拟机栈发挥的作用是类似的，它们之间的区别不过是虚拟机栈为虚拟机执行java方法（也就是字节码）服务，而本地方法栈则为虚拟机使用的Native方法服务。

　　2、线程共享区

　　　a、Java堆

　　　　被所有线程共享的一块内存区域，也是Java虚拟机所管理的内存中最大的一块。

　　　b、方法区

　　　　用于存储已被虚拟机加载的类信息、常量、静态变量、即时编辑器编译后的代码等数据，虽然Java虚拟机规范把方法区描述为堆的一个逻辑部分，但是它却有一个别名Non-Heap(非堆)

　　下面开始说正题

　　目前虚拟机基本都是采用可达性算法，为什么不采用引用计数算法呢？下面就说说引用计数法是如何统计所有对象的引用计数的，再对比分析可达性算法是如何解决引用技术算法的不足。先简单说说这两个算法：

　　1、引用计数法(reference-counting)：每个对象都有一个引用计数器，当对象被引用一次，计数器就加1，当对象引用时效一次就减，当计数器为0，意味着对象是垃圾对象，可以被GC回收。

　　2、可达性算法（GC Root Tracing）：从GC Root作为起点开始搜索，那么整个连通图中对象都是活的，对于GC Root无法达到的对象便是垃圾对象，随时可被GC回收。

　　采用引用计数算法的系统只需在每个实例对象创建之初，通过计数器来记录所有的引用次数即可。而可达性算法，则需要再次GC时，遍历整个GC根节点来判断是否回收。

　　下面通过一段代码来对比说明：

　　

 public class GcDemo {

    public static void main(String[] args) {
        //分为6个步骤
        GcObject obj1 = new GcObject(); //Step 1
        GcObject obj2 = new GcObject(); //Step 2

        obj1.instance = obj2; //Step 3
        obj2.instance = obj1; //Step 4

        obj1 = null; //Step 5
        obj2 = null; //Step 6
    }
}

class GcObject{
    public Object instance = null;
}

　　1、引用计数算法

　　如果采用的是引用计数算法：

　　再回到前面代码GcDemo的main方法共分为6个步骤：

• Step1：GcObject实例1的引用计数加1，实例1的引用计数=1；
• Step2：GcObject实例2的引用计数加1，实例2的引用计数=1；
• Step3：GcObject实例2的引用计数再加1，实例2的引用计数=2；
• Step4：GcObject实例1的引用计数再加1，实例1的引用计数=2；

　　执行到Step 4，则GcObject实例1和实例2的引用计数都等于2。

　　接下来继续结果图：
　　

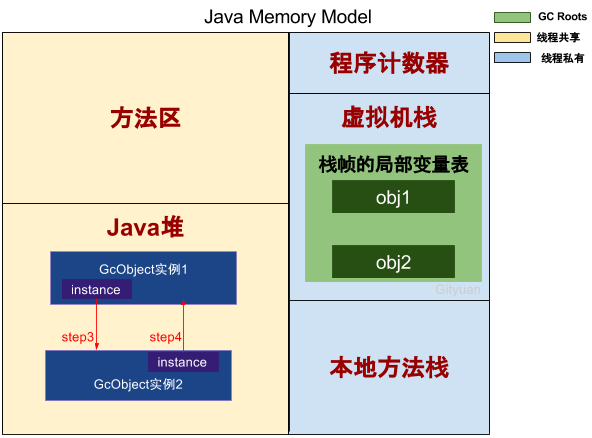
• Step5：栈帧中obj1不再指向Java堆，GcObject实例1的引用计数减1，结果为1；
• Step6：栈帧中obj2不再指向Java堆，GcObject实例2的引用计数减1，结果为1。

　　到此，发现GcObject实例1和实例2的计数引用都不为0，那么如果采用的引用计数算法的话，那么这两个实例所占的内存将得不到释放，这便产生了内存泄露。

　　

　　2、可达性算法

　　这是目前主流的虚拟机都是采用GC Roots Tracing算法，比如Sun的Hotspot虚拟机便是采用该算法。 该算法的核心算法是从GC Roots对象作为起始点，利用数学中图论知识，图中可达对象便是存活对象，

　　而不可达对象则是需要回收的垃圾内存。这里涉及两个概念，一是GC Roots，一是可达性。

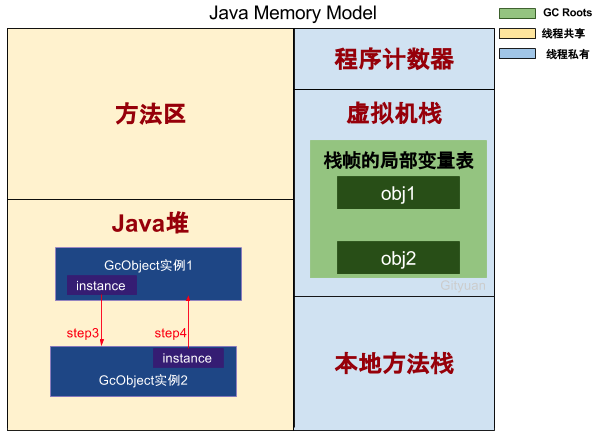
　　那么可以作为GC Roots的对象（见下图）：

• 虚拟机栈的栈帧的局部变量表所引用的对象；
• 本地方法栈的JNI所引用的对象；
• 方法区的静态变量和常量所引用的对象；

　　关于可达性的对象，便是能与GC Roots构成连通图的对象，如下图：
　　

　　从上图，reference1、reference2、reference3都是GC Roots，可以看出：

• reference1-> 对象实例1；
• reference2-> 对象实例2；
• reference3-> 对象实例4；
• reference3-> 对象实例4 -> 对象实例6；

　　可以得出对象实例1、2、4、6都具有GC Roots可达性，也就是存活对象，不能被GC回收的对象。
　　而对于对象实例3、5直接虽然连通，但并没有任何一个GC Roots与之相连，这便是GC Roots不可达的对象，这就是GC需要回收的垃圾对象。

　　到这里，相信大家应该能彻底明白引用计数算法和可达性算法的区别吧。

　　再回过头来看看最前面的实例，GcObject实例1和实例2虽然从引用计数虽然都不为0，但从可达性算法来看，都是GC Roots不可达的对象。

　　总之，对于对象之间循环引用的情况，引用计数算法，则GC无法回收这两个对象，而可达性算法则可以正确回收。

　　参考资料：https://blog.csdn.net/lamp_zy/article/details/53212909