BUAA_OO_homworkone包含三角函数的多项式求导

第一次作业

基于x的简单多项式相加求导

• 带符号整数 支持前导0的带符号整数，符号可省略，如： +02、-16>、19260817等。
• 幂函数
  • 一般形式 由自变量x和指数组成，指数为一个带符号整数，如：x ^ +2。
  • 省略形式 当指数为1的时候，可以采用省略形式，如：x。
• 项表达式 由加法和减法运算符连接若干项组成，如： -1 + x ^ 233 - x ^ >06。此外，在第一项之前，可以带一个正号或者负号，如：- -1 + x ^ 233>、+ -2 + x ^ 19260817。注意，空串不属于合法的表达式。
  • 变量项
    • 带有系数的幂函数，如：2 * x ^ 2、-1 * x。
    • 系数为1的时候，可以省略系数或表示为正号开头的形式，如：x ^ 2、+ >x ^ 2。
    • 系数为-1的时候，可以表示为负号开头的形式，如：-x ^ 2。
  • 常数项 包含一个带符号整数，如：233。
• 空白字符 在本次作业中，空白字符包含且仅包含<space>和\t。

此外，值得注意的几点是：

• 带符号整数内不允许包含空白字符。
• 幂函数、项、表达式，在不与上一条矛盾的前提下，可以在任意位置包含任意数量的>空白字符。
• 如果某表达式存在不同的解释方式，则只要有任意一条解释中是合法的，该表达式即>为合法。

题目分析与程序设计

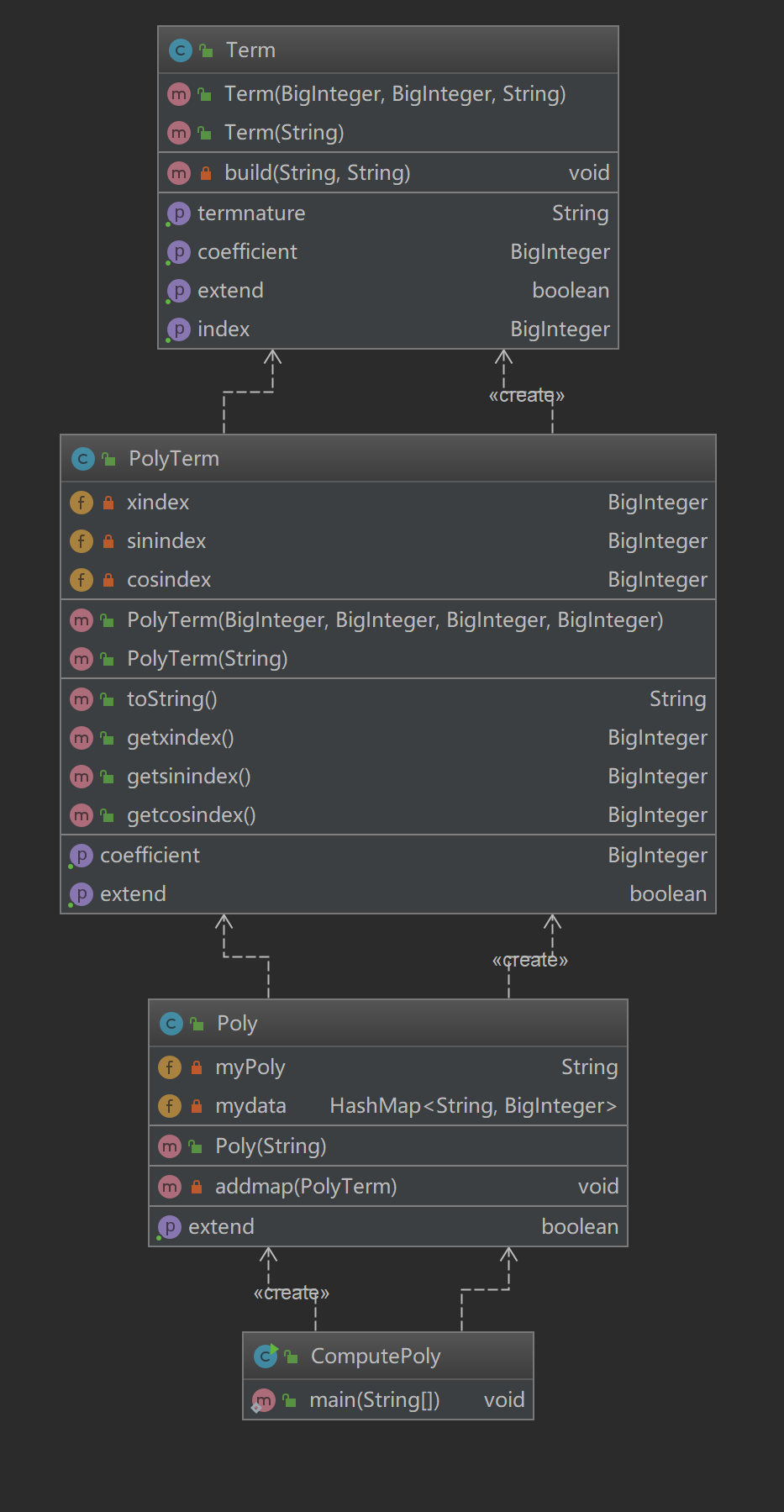
基础底的PolyTerm类系数coefficient和指数index以及extend判断项是否表达式合法

传入一段字符串进行构造，比如+4*x^-5

上层类的Poly包含结果String类myPoly，以及用来多项式每一项存储结果的HashMap

将多项式用加号分割然后分割的每一项先求导构造Poly类，将构造出来的Poly类的coefficient和index存入HashMap

再从HashMap遍历构造myPoly字符串

ComputePoly是main主类将stdin的string用来构造Poly

总结整理和反思

第一次写面向对象程序，代码复用性较差，用加号分割会出现一些bug，比如^+,^-,要预先将它替换

PolyTerm没有写求导方式而是直接用表达式写出代码可移植性差

第二次作业

第二次作业,增加了三角函数的处理，额外的格式规定。

• 三角函数 sin(x)或cos(x)（在本次作业中，括号内仅为x）
  • 一般形式 类似于幂函数，由sin(x)和指数组成，指数为一个带符号整数，如：sin(x) ^ +2。
  • 省略形式 当指数为1的时候，可以采用省略形式，省略指数部分，如：sin(x)。
• 常数因子 包含一个带符号整数，如：233。
• 项
  • 一般形式 由乘法运算符连接若干因子组成，如：2 * x ^ 2 * 3 * x ^ -2、sin(x) * cos(x) * x。

此外，值得注意的几点是：

• 三角函数的保留字内不允许包含空白字符，即sin和cos内不可以含有空白字符。
• 未知数包含且仅包含小写的x。

题目分析与程序设计

第二次作业我想继承第一次作业的思路，我用加号分割项，用乘号分割因子

发现一个奇特的地方，每一项都是由x，sin(x),cos(x)组成的

(x^a*sin(x)^b*cos(x)^c)'=a*x^a-1*sin(x)^b*cos(x)^c+b*x^a*sin(x)^b-1*cos(x)^c+c*x^a*sin(x)^b*cos(x)^c-1

Term:继承上一次作业加入了termnature，参数是x,sin(x),cos(x)用来存储基础因子

PolyTerm:是构造形如d*x^a*sin(x)^b*cos(x)^c  的表达式一共四个值 coefficient，xindex，sinindex和cosindex，以及重构toString,输出x^a*sin(x)^b*cos(x)^c

因为我们要用toString作为存储HashMap的键值，对于传进来的String我们要用*分割然后遍历每个因子改变四个值coefficient，xindex，sinindex和cosindex

Poly:将输入多项式每一项用加号分割，对于分割的每一项构造PolyTerm化简，然后传出参数，用上面公式求导构造三个PolyTerm项

以toString为key值，coefficient为value存在HashMap

总结整理和反思

相比于第一次作业 *出现+也要预先处理，对于字符串的处理没有进行三角函数的化简

第三次作业

第三次作业加入了可以嵌套的递归规则

• 变量因子

  • 幂函数

    • 一般形式 由自变量x和指数组成，指数为一个带符号整数，如：x ^ +2。且，指数绝对值一律不得超过​。

    • 省略形式 当指数为1的时候，可以采用省略形式，如：x。

  • 三角函数 sin(x)，cos(x)，另外，本指导书范围内所有的词语“三角函数”，除非特殊说明，否则一律包含且仅包含上述两个函数）

    • 一般形式 类似于幂函数，由sin(x)，cos(x) 和指数组成，指数为一个带符号整数，如：sin(x) ^ +2。同样的，指数绝对值一律不得超过​。

    • 省略形式 当指数为1的时候，可以采用省略形式，省略指数部分，如：sin(x)。

• 常数因子 包含一个带符号整数，如：233。

• 表达式因子 将在表达式的相关设定中进行详细介绍。不过，表达式因子不支持幂运算。

• 嵌套因子 本次作业将支持因子嵌套在三角函数因子里面，即一个因子作为另一个三角函数因子的自变量，例如sin(x^2)，cos(sin(x)) 以及 sin(sin(cos(cos(x^2))))^2 等。但是不允许出现指数为变量的情况，指数依然只能是带符号整数，例如sin(x) ^ sin(x)是不合法的，因为指数不是自变量。也不允许幂函数的自变量为除了x之外的因子，例如1926^0817是不合法的，因为幂函数的自变量只能为x。

题目分析与程序设计

第三次作业我依旧想继承第二次作业的思想，我用加号分割项用乘号分割因子，但是因子遇到了嵌套的情况，所以用括号再递归分割因子

Pol类用来把顶层类我们的表达式用加号分割成每一项

对于每个项求导我们要用到链式法则和复合函数求导规则，我用用乘号分割因子，每个因子构造顶层Po用一个循环实现链式法则求导

如果遇到符合第二次作业的PolyTerm没有出现嵌套规则的可以直接求导

如果遇到嵌套我们利用复合函数求导规则f(g(x)) ' = derva(f(x))derva(g(x))

我用一个简化算法节省复杂度把g(x)替换成x既可f(x)可以直接构造PolyTerm求导，然后再替换回来可以节省复杂度

首先为了防止因为括号内的加号和乘号或者sin(x)*cos(x)，影响我的分割我采用一个堆栈维护括号匹配