Python之算法基础

1》递归相关：

　　递归：递归算法是一种直接或间接地调用自身算法的过程，在计算机编写程序中，递归算法对解决一大类问题是十分有效的，它往往使算法的描述简洁而且                   易于理解；
　　特点：

　　　　（1）递归就是在过程或函数中调用自身；
　　　　（2）在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口；
　　　　（3）递归算法解题通常显得很简洁，但递归算法解题的运行效率较低，所以一般不提倡使用递归算法设计程序；
　　　　（4）在递归调用的过程当中系统为每一层的返回点，局部量等开辟了栈来存储，递归次数过多容易造成栈溢出等，所以一般不提倡使用递归算法设计                          程序；
　　要求：
　　　　递归算法所体现的“重复”一般有三个要求：
　　　　（1）每次调用在规模上都有所缩小（通常是减半）；
　　　　（2）相邻两次重复直接有紧密的联系，前一次要为后一次做准备（通常前一次的输出就作为后一次的输入）；
　　　　（3）在问题的规模极小时必须用直接给出解答而不再进行递归调用，因而每次递归调用都是有条件的（以规模未达到直接解答的大小为条件），无条                          件递归调用将会成为死循环而不能正常结束；
　　示例：

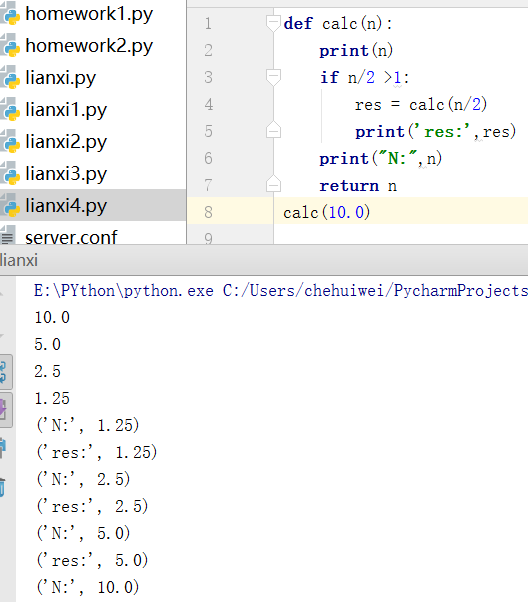
2》通过递归实现裴波那契数列（每个数总是等于前两个数的值的数列）：

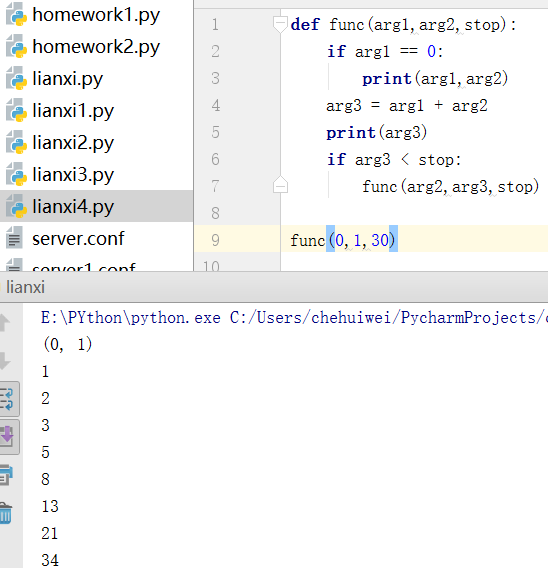
3》算法基础之二分查找：

上图会找不到1，现做出改正：

　　　　　　 

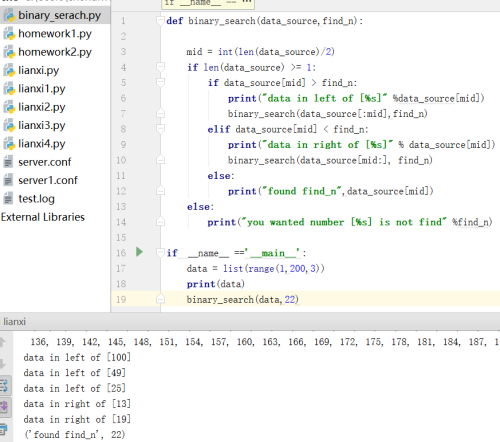
4》算法基础之二维数组：

1>生成列表方法：

　　　　　　

　　     2>生成二维数组方法：

　　　　　　

　　　　　　   eg:将一个二维数组翻转90度：
　　　　　　　　自己做的：

　　　　　　　　   

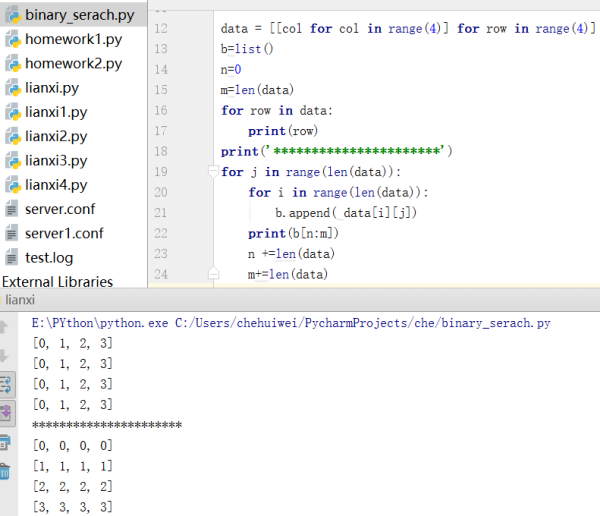
参考老师代码：

　　　　　　　　　　　　

5》算法基础之冒泡排序：

　　　　

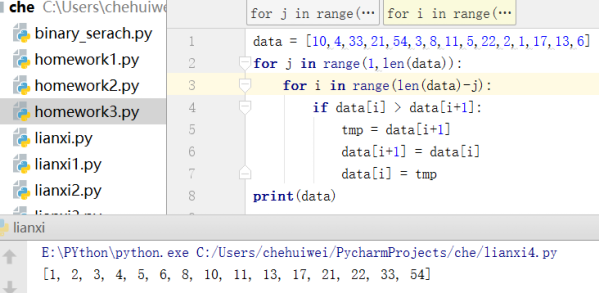
6》时间复杂度介绍：　　

　 1>时间频度：

　　　 　一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机进行测试才能知道，当我们可能也没有必要对每个算法都上机测试，只需知道哪个算           法花费等待时间多，哪个算法花费的时间少就可以了；并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费             时间就多，一个算法中的语句执行次数称为语句频度或者时间频度，记为T(n)；
　2>时间复杂度：
　　　　在刚才提到的时间频度中，n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化；但有时我们也想指定它变化时呈现什么规律，为此，我们            引入时间复杂度概念；一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大              时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数，记作T(n)=O(f(n)),称O(f(n))为算法的渐进时
          间复杂度，简称时间复杂度；
　3>指数时间：
　　指的是一个问题求解所需要的计算时间m(n),依输入数据的大小n而呈指数成长（即输入数据的数量依线性成长，所花的时间将会以指数成长）
　4>示例：

         第一个for循环的时间复杂度为O(n),第二个for循环的时间复杂度为O(n^2),则整个算法的时间复杂度为O(n+n^2)=O(n^2);              

　　5>常数时间：
　　　　若对于一个算法，T(n)的上界与输入大小无关，则称其具有常数时间，记作O(1)时间；一个例子是访问数组中的单个元素，因为访问它只需要一条指             令，但是，找到无序数组中的最小元素则不是，因为这需要遍历所有元素找到最小值，这是一项线性时间的操作，或称O(n)时间；但如果预先知道元素的数          量并假设数量保持不变，则该操作也可被称为具有常数时间；
      6>对数时间：
　　　　若算法的T(n)=O(log n),则称其具有对数时间；常见的具有对数时间的算法有二叉树的相关操作和二分搜索；对数时间的算法是非常有效的，因为每增加         一个输入，其所需要的额外计算时间会变小；递归将字符串砍半并且输出是这个类别函数的一个简单例子；
     7>线性时间：
　　　　如果一个算法的时间复杂度为O(n),则称这个算法具有线性时间，或O(n)时间，非正式地说，这意味着
             对于足够大的输入，运行时间增加的大小与输入成线性关系。例如，一个计算列表所有元素的和的程序，需要的时间与列表的长度成正比；