Codeforces 932.D Tree

D. Tree

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

You are given a node of the tree with index 1 and with weight 0. Let cnt be the number of nodes in the tree at any instant (initially, cnt is set to 1). Support Q queries of following two types:

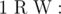•  Add a new node (index cnt + 1) with weight W and add edge between node R and this node.
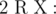•  Output the maximum length of sequence of nodes which
  1. starts with R.
  2. Every node in the sequence is an ancestor of its predecessor.
  3. Sum of weight of nodes in sequence does not exceed X.
  4. For some nodes i, j that are consecutive in the sequence if i is an ancestor of j then w[i] ≥ w[j] and there should not exist a node k on simple path from i to j such that w[k] ≥ w[j]

The tree is rooted at node 1 at any instant.

Note that the queries are given in a modified way.

Input

First line containing the number of queries Q (1 ≤ Q ≤ 400000).

Let last be the answer for previous query of type 2 (initially last equals 0).

Each of the next Q lines contains a query of following form:

• 1 p q (1 ≤ p, q ≤ 1018): This is query of first type where 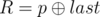 and 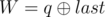. It is guaranteed that 1 ≤ R ≤ cnt and0 ≤ W ≤ 109.
• 2 p q (1 ≤ p, q ≤ 1018): This is query of second type where 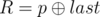 and 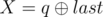. It is guaranteed that 1 ≤ R ≤ cntand 0 ≤ X ≤ 1015.

 denotes bitwise XOR of a and b.

It is guaranteed that at least one query of type 2 exists.

Output

Output the answer to each query of second type in separate line.

Examples

input

6
1 1 1
2 2 0
2 2 1
1 3 0
2 2 0
2 2 2

output

0
1
1
2

input

6
1 1 0
2 2 0
2 0 3
1 0 2
2 1 3
2 1 6

output

2
2
3
2

input

7
1 1 2
1 2 3
2 3 3
1 0 0
1 5 1
2 5 0
2 4 0

output

1
1
2

input

7
1 1 3
1 2 3
2 3 4
1 2 0
1 5 3
2 5 5
2 7 22

output

1
2
3

Note

In the first example,

last = 0

- Query 1: 1 1 1, Node 2 with weight 1 is added to node 1.

- Query 2: 2 2 0, No sequence of nodes starting at 2 has weight less than or equal to 0. last = 0

- Query 3: 2 2 1, Answer is 1 as sequence will be {2}. last = 1

- Query 4: 1 2 1, Node 3 with weight 1 is added to node 2.

- Query 5: 2 3 1, Answer is 1 as sequence will be {3}. Node 2 cannot be added as sum of weights cannot be greater than 1. last = 1

- Query 6: 2 3 3, Answer is 2 as sequence will be {3, 2}. last = 2

题目大意：一棵树,每个点有点权，两种操作：1.新加一个点连接r,权值为w.  2.从一个点r开始往祖先上跳，每次跳到第一个值≥自身的祖先，将跳到的点的和加起来，不能大于w,问能跳几次.

分析：挺有意思的一道题.

　　　暴力算法就是一个一个往上跳着找喽，在树上往上跳有一种常用的优化方法--倍增.在这道题里面可以倍增地跳到≥自身权值的点.

　　　考虑怎么实现，fa数组就不能记录第2^i个祖先了，而要记录比自身权值大的第2^i个祖先.在加点的时候处理.可以发现，一旦处理出fa[i][0],就能够根据祖先节点的信息推出fa[i][j].

　　　如何处理fa[i][0]?如果r的权值比新加的点i的权值大或相等，则fa[i][0] = r，否则从r开始往上跳，如果w[fa[r][j]] < w[i],则往上跳，最后fa[i][0] = fa[r][0].

　　　因为最后要求和嘛，可以顺便维护一个sum数组，表示从i这个点跳到比i权值大的第2^j个祖先跳到的点的权值和为多少. 求出了这两个数组以后查询就很好办了，sum[i][j]是否≤w,是的话就往上跳，并且w -= sum[i][j].倍增的基础应用嘛.

　　　想清楚如何加速往祖先跳的过程，以及倍增应该维护什么东西这道题就能解决了.

　　　一些边界的值需要特殊考虑！

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;
const ll maxn = ,inf = 1e18;
ll q,lastans,cnt = ,w[maxn];
ll fa[maxn][],sum[maxn][];

void add(ll x,ll v)
{
    w[++cnt] = v;
    if (w[cnt] <= w[x])
        fa[cnt][] = x;
    else
    {
        int y = x;
        for (int i = ; i >= ; i--)
        {
            if (w[fa[y][i]] < w[cnt])
                y = fa[y][i];
        }
        fa[cnt][] = fa[y][];
    }
    if (fa[cnt][] == )
        sum[cnt][] = inf;
    else
        sum[cnt][] = w[fa[cnt][]];
    for (int i = ; i <= ; i++)
    {
        fa[cnt][i] = fa[fa[cnt][i - ]][i - ];
        if (fa[cnt][i] == )
            sum[cnt][i] = inf;
        else
            sum[cnt][i] = sum[cnt][i - ] + sum[fa[cnt][i - ]][i - ];
    }
}

ll query(ll x,ll v)
{
    if (w[x] > v)
        return ;
    v -= w[x];
    ll res = ;
    for (int i = ; i >= ; i--)
    {
        if (v >= sum[x][i])
        {
            v -= sum[x][i];
            res += ( << i);
            x = fa[x][i];
        }
    }
    return res;
}

int main()
{
    w[] = inf;
    for (int i = ; i <= ; i++)
        sum[][i] = inf;
    scanf("%I64d",&q);
    while (q--)
    {
        int id;
        ll a,b;
        scanf("%d",&id);
        scanf("%I64d%I64d",&a,&b);
        a ^= lastans;
        b ^= lastans;
        if (id == )
            add(a,b);
        else
            printf("%I64d\n",lastans = query(a,b));
    }
}