[洛谷P2745] [USACO5.3]窗体面积Window Area

洛谷题目链接:[USACO5.3]窗体面积Window Area

题目描述

你刚刚接手一项窗体界面工程。窗体界面还算简单，而且幸运的是，你不必显示实际的窗体。有 5 种基本操作：

创建一个新窗体

将窗体置顶

将窗体置底

删除一个窗体

输出窗体可见部分的百分比（就是，不被其它窗体覆盖的部分）。

在输入文件中，操作以如下的格式出现。

创建一个新窗体：w(I,x,y,X,Y)

将窗体置顶： t(I)

将窗体置底： b(I)

删除一个窗体：d(I)

输出窗体可见部分的百分比：s(I)

I 是每个窗体唯一的标识符，标识符可以是 'a'..'z', 'A'..'Z' 和 '0'..'9' 中的任何一个。输入文件中没有多余的空格。

（x,y）和（X,Y）是窗体的对角。当你创建一个窗体的时候，它自动被“置顶”。你不能用已经存在的标识符来创建窗体，但是你可以删除一个窗体后再用已删除窗体的标识符来创建窗体。坐标用正整数来表示，并且所有的窗体面积都不为 0（x <> X 且 y <> Y）。x 坐标和 y 坐标在 1 —— 32767 的范围内。

输入输出格式

输入格式：

输入文件包含给你的解释程序的一系列命令，每行一个。当输入文件结束时，停止程序。

输出格式：

只对于 s(I) 命令进行输出。当然，输入文件可能有许多 s(I) 命令(不超过500次)，所以输出文件应该是一个百分比的序列，每行一个，百分比是窗体可见部分的百分比。百分比应该四舍五入到三位小数。

输入输出样例

输入样例#1：

w(a,10,132,20,12)

w(b,8,76,124,15)

s(a)

输出样例#1：

49.167

说明

题目翻译来自NOCOW。

USACO Training Section 5.3

题解: 这里使用了一种叫做上浮法的算法.

考虑当前要上浮的矩形在第\(k\)层,需要上升到第\(k-1\)层,那么它上面的矩形和它只有两种情况:相交或者不相交,显然不相交的情况可以不用考虑,直接将它提到第\(k-1\)层就可以了.

那么相交的情况怎么处理呢?我们来看一下下面这张图:

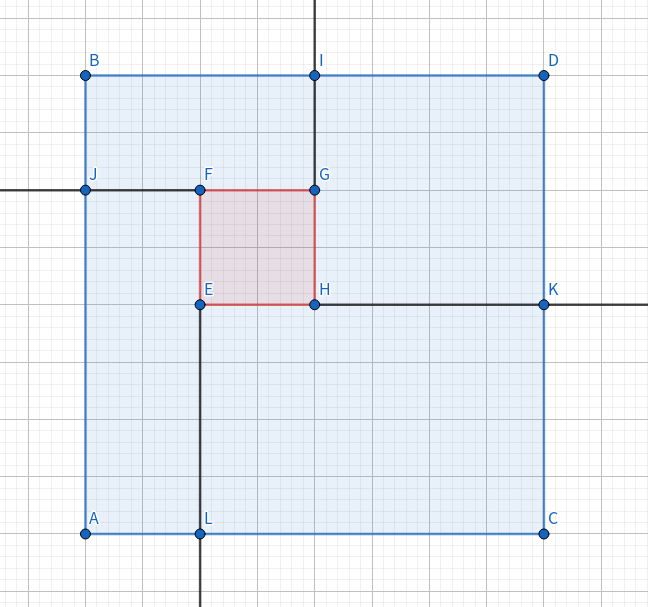
图中蓝色的是我们正在上浮的矩形\(B(blue)\),红色的是在\(R(red)\)上面一层挡住\(B\)一部分面积的矩形\(R\),我们可以发现,只要\(R,B\)有交集,那么就可以根据\(R\)的上下左右边将\(B\)分成几个矩形继续上浮(其他的情况可以自己手画一下,因为作图有点麻烦就不再举例子了).

那么根据这个原理,我们就可以将正在上升的矩形分为最多\(4\)部分继续上浮,这一过程可以用\(dfs\)来实现,具体实现看一下代码.

void dfs(int k, int x1, int y1, int x2, int y2){
    if(x1 == x2 || y1 == y2) return; // 判断递归的边界条件
    if(!k){ ans += (double)(x2-x1)*(y2-y1); return; }
    int a1 = a[k].x1, b1 = a[k].y1, a2 = a[k].x2, b2 = a[k].y2;
    if(a2 < x1 || a1 > x2 || b2 < y1 || b1 > y2){
        dfs(k-1, x1, y1, x2, y2); return; // 无交集直接继续下一层不需要回溯
    }
    if(a1 <= x1 && b1 <= y1 && x2 <= a2 && y2 <= b2) return; // 已经被某个矩形完全覆盖了那么就不可能被看到了,直接return
    dfs(k-1, x1, min(y2, b2), min(x2, a2), y2); // up
    dfs(k-1, min(x2, a2), max(y1, b1), x2, y2); // right
    dfs(k-1, max(x1, a1), y1, x2, max(y1, b1)); // down
    dfs(k-1, x1, y1, max(x1, a1), min(y2, b2)); // left
    //这里的四个dfs就是将正在上浮的矩形分割的过程,参数可以自己画几个栗子模拟一下
}

知道了如何统计矩形面积,剩下的只需要模拟一下就好了.

#include<bits/stdc++.h>
using namespace std;
const int N = 100;
// N只有100是因为窗口标识符只有大小写字母和0到9
int used[300], cnt = 0;
double ans = 0, tot = 0;
struct window{
    int x1, x2, y1, y2; char c;
    window(int _x1 = 0, int _y1 = 0, int _x2 = 0, int _y2 = 0, int _c = 0){
        x1 = _x1, y1 = _y1, x2 = _x2, y2 = _y2, c = _c;
    }
    bool operator == (const window &a) const {
        return c == a.c;
    }
    bool operator < (const window &a) const {
        if(x1 != a.x1) return x1 < a.x1;
        if(y1 != a.y1) return y1 < a.y1;
        if(x2 != a.x2) return x2 < a.x2;
        return y2 < a.y2;
    }
}a[N], win[300];
void move(window x, int f){
    int pos = 0;
    for(int i = 1; i <= cnt; i++)
        if(a[i] == x){ pos = i; break; }
    if(f == 0) for(int i = pos; i >= 2; i--) swap(a[i], a[i-1]);
    else for(int i = pos; i < cnt; i++) swap(a[i], a[i+1]);
}
void delet(window x){
    int pos;
    for(int i = 1; i <= cnt; i++)
        if(a[i] == x) pos = i;
    used[x.c] = 0, win[x.c] = (window){ 0, 0, 0, 0, 0 };
    for(int i = pos+1; i <= cnt; i++) a[i-1] = a[i];
    cnt--;
}
void dfs(int k, int x1, int y1, int x2, int y2){
    if(x1 == x2 || y1 == y2) return;
    if(!k){ ans += (double)(x2-x1)*(y2-y1); return; }
    int a1 = a[k].x1, b1 = a[k].y1, a2 = a[k].x2, b2 = a[k].y2;
    if(a2 < x1 || a1 > x2 || b2 < y1 || b1 > y2){
        dfs(k-1, x1, y1, x2, y2); return;
    }
    if(a1 <= x1 && b1 <= y1 && x2 <= a2 && y2 <= b2) return;
    dfs(k-1, x1, min(y2, b2), min(x2, a2), y2); // up
    dfs(k-1, min(x2, a2), max(y1, b1), x2, y2); // right
    dfs(k-1, max(x1, a1), y1, x2, max(y1, b1)); // down
    dfs(k-1, x1, y1, max(x1, a1), min(y2, b2)); // left
}
int main(){
    char opt, id; int x1, y1, x2, y2, pos; window tmp;
    while(cin >> opt){
        if(opt == 's'){
            scanf("(%c)", &id); pos = 0;
            for(int i = 1; i <= cnt; i++)
                if(a[i] == win[id]) pos = i;
            ans = 0, tot = (double)(a[pos].x2-a[pos].x1)*(a[pos].y2-a[pos].y1);
            dfs(pos-1, a[pos].x1, a[pos].y1, a[pos].x2, a[pos].y2);
            cout << fixed << setprecision(3) << ans*100/tot << endl;
        } else {
            scanf("(%c,%d,%d,%d,%d)", &id, &x1, &y1, &x2, &y2);
            if(x1 > x2) swap(x1, x2); if(y1 > y2) swap(y1, y2);
            tmp = (window){ x1, y1, x2, y2, id };
            if(opt == 'w'){
                if(used[id]) continue;
                win[id] = a[++cnt] = tmp, move(tmp, 0);
            }
            if(opt == 't') move(tmp, 0);
            if(opt == 'b') move(tmp, 1);
            if(opt == 'd') delet(tmp);
        }
        opt = getchar();
    }
    return 0;
}