HDU4719-Oh My Holy FFF(DP线段树优化)

Oh My Holy FFF

Time Limit: 5000/2500 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)

Total Submission(s): 606    Accepted Submission(s): 141

Problem Description

N soldiers from the famous "*FFF* army" is standing in a line, from left to right.

 o   o   o   o   o   o   o   o   o   o   o   o   o   o   o   o   o   o
/F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\
/ \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \

You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:

 o   o   o  |  o   o   o   o  |  o   o   o   o   o   o  |  o   o   o   o   o
/F\ /F\ /F\ | /F\ /F\ /F\ /F\ | /F\ /F\ /F\ /F\ /F\ /F\ | /F\ /F\ /F\ /F\ /F\
/ \ / \ / \ | / \ / \ / \ / \ | / \ / \ / \ / \ / \ / \ | / \ / \ / \ / \ / \

In your opinion, the number of soldiers in each group should be no more than L.

Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That
is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be b_i > b_i-1.

You give your division a score, which is calculated as 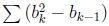, b₀ = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.

Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.

 

Input

The first line has a number T (T <= 10) , indicating the number of test cases.

For each test case, first line has two numbers N and L (1 <= L <= N <= 10⁵), as described above.

Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= H_i <= 10⁵)

 

Output

For test case X, output "Case #X: " first, then output the best score.

 

Sample Input

2
5 2
1 4 3 2 5
5 2
5 4 3 2 1

 

Sample Output

Case #1: 31
Case #2: No solution

 

题意：n(n < 1e5)个人排成一行，把它切成若干堆。要求每一堆的长度不超过l(l < 1e5),而且每一堆的最右一个人的身高都要比前一堆的最右一个人的身高要高，对于每一种方案，它的分数是SUM(b[k]^2-b[k-1] )  b[k] 为第k堆最右一个人的身高 要求最高的分数。

思路：朴素的DP 是  DP[i]  = max(DP[j] - b[j]) + b[i]*b[i]  ( i-l <=  j <= i-1 )  可是这样会超时（O(n^2)） 能够发现每次求DP[i] 的时候 实际就是求 区间[i-l,i-1]  DP[j]-b[j]的最大值，因此能够利用线段树优化。此时还须要解决一个问题：就是怎样保证每次求DP[i]的时候保证区间[i-l,i-1]
的每一个人的身高都是比自己矮的？  能够进行先排序。让矮的人先选，假设身高一样就让序号在后的先选，这样就不会有冲突了（单点更新的时候）。 每次查询的时候单点更新就可以。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
#define REP(_,a,b)  for(int _=(a); _<=(b);++_)
#define sz(s) (int)((s).size())
typedef long long ll;
const int maxn = 1e5+10;
int n,l;
ll dp[maxn];
struct Num{
	ll h;
	int idx;
	Num(ll h = 0,int idx = 0):h(h),idx(idx){}
	friend bool operator < (Num a,Num b){
		if(a.h!=b.h) return a.h < b.h;
		else return a.idx > b.idx;
	}
};
vector<Num> vN;
struct node{
	int lson,rson;
	ll maxx;
	int mid(){
		return (lson+rson)>>1;
	}
}tree[maxn*4];
void pushUp(int rt){
	tree[rt].maxx = max(tree[rt<<1].maxx,tree[rt<<1|1].maxx);
} 

void build(int L,int R,int rt){
	tree[rt].lson = L;
	tree[rt].rson = R;
	tree[rt].maxx = -1;
	if(L==R){
		return;
	}
	int mid = tree[rt].mid();
	build(L,mid,rt<<1);
	build(mid+1,R,rt<<1|1);
}
void init(){
	vN.clear();
	memset(dp,-1,sizeof dp);
}
void update(int pos,int l,int r,int rt,ll x){
	if(l==r){
		tree[rt].maxx = x;
		return;
	}
	int mid = tree[rt].mid();
	if(pos<=mid){
		update(pos,l,mid,rt<<1,x);
	}else{
		update(pos,mid+1,r,rt<<1|1,x);
	}
	pushUp(rt);
}
ll query(int L,int R,int l,int r,int rt){
	if(L <=l && R >= r){
		return tree[rt].maxx;
	}
	int mid = tree[rt].mid();
	ll ret;
	bool flag = false;
	if(L <= mid){
		ret = query(L,R,l,mid,rt<<1);
		flag = true;
	}
	if(R > mid){
		if(flag){
			ret = max(ret,query(L,R,mid+1,r,rt<<1|1));
		}else{
			ret = query(L,R,mid+1,r,rt<<1|1);
		}
	}
	return ret;
}
void input(){
	scanf("%d%d",&n,&l);
	REP(_,1,n){
		ll h;
		scanf("%I64d",&h);
		vN.push_back(Num(h,_));
	}
	sort(vN.begin(),vN.end());
	build(0,n,1);
}
void solve(){
	update(0,0,n,1,0);
	REP(_,0,sz(vN)-1) {
		int ni = vN[_].idx;
		ll nh = vN[_].h;
		ll tm = query(max(ni-l,0),ni-1,0,n,1);
		if(tm>=0){
			dp[ni] = tm+nh*nh;
			update(ni,0,n,1,dp[ni]-nh);
		}
		if(ni==n) break;
	}
	if(dp[n]<=0){
		printf("No solution\n");
	}else{
		printf("%I64d\n",dp[n]);
	}
}
int main(){
	int ncase,T=1;
	cin >> ncase;
	while(ncase--){
		init();
		input();
		printf("Case #%d: ",T++);
		solve();
	}
	return 0;
}