Codeforces Round #257 (Div. 2) B Jzzhu and Sequences

Jzzhu has invented a kind of sequences, they meet the following property:

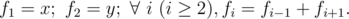
You are given x and
y, please calculate f_n modulo
1000000007 (10⁹ + 7).

Input

The first line contains two integers x and
y (|x|, |y| ≤ 10⁹). The second line contains a single integer
n (1 ≤ n ≤ 2·10⁹).

Output

Output a single integer representing f_n modulo
1000000007 (10⁹ + 7).

Sample test(s)

Input

2 3
3

Output

1

Input

0 -1
2

Output

1000000006

Note

In the first sample, f₂ = f₁ + f₃,
3 = 2 + f₃,
f₃ = 1.

In the second sample, f₂ =  - 1;
 - 1 modulo (10⁹ + 7) equals
(10⁹ + 6).

详见代码。

。。

#include<iostream>
using namespace std;
#define  modulo 1000000007
int main()
{
  __int64 q[6];
  int m,n;
	  int k;
  while(~scanf("%d%d",&m,&n))
  {
     q[1]=m;
	 q[2]=n;
	 q[3]=n-m;
	 q[4]=-m;
	 q[5]=-n;
	 q[0]=m-n;
	 cin>>k;
	 k=k%6;
	 while(q[k]<0)
		 q[k]=q[k]+modulo;

		 printf("%I64d\n",q[k]%modulo);
  }
return 0;
}

版权声明：本文博客原创文章。博客，未经同意，不得转载。