主席树（可持久化线段树） 静态第k大

可持久化数据结构介绍

可持久化数据结构是保存数据结构修改的每一个历史版本，新版本与旧版本相比，修改了某个区域，但是大多数的区域是没有改变的，

所以可以将新版本相对于旧版本未修改的区域指向旧版本的该区域，这样就节省了大量的空间，使得可持久化数据结构的实现成为了可能。

如下图，就是可持久化链表

插入前

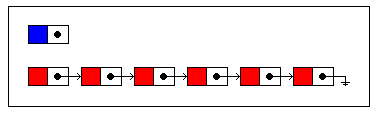
插入后

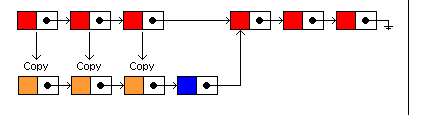
尽可能利用历史版本和当前版本的相同区域来减少空间的开销。

而主席树（可持久化线段树）的原理同样是这样。

有n个数字，  我们将其离散化，那么总有[1,n]个值，如果建一棵线段树，每个结点维护子树中插入的值的个数。 求总区间第k大

那么如果k>=左子树中值的个数，那么就去左子树中找，   否则就去右子树中找第（k-左子树值的个数）大值。

如果要求区间[l,r]第k大，那么就要维护n棵线段树

每棵线段树维护的都是[1,n]值出现的个数， 所以每棵线段树的形态结构是相同的

第i棵线段树的根为T[i] ， 维护的是前i个数字离散化后出现的次数。

那么主席树有两个性质

线段树的每个结点，保存的都是这个区间含有的数字的个数

主席树的每个结点，也就是每棵线段树的大小和形态是一样的，也就是主席树的每个结点（线段树与线段树之间）是可以相互进行加减运算的

假设要求区间[l,r]的第k大, T[r]左子树值的个数 - T[l-1]左子树值的个数大于>=k  ,  那么就说明  区间[l,r]的数离散化后有大于n个数插入了左子树，

所以应该去左子树去找第k个大， 反之，去右子树找 第(k- (T[r]左子树值的个数 - T[l-1]左子树值的个数) )大。

至于主席树的构建， 第T[i+1]棵树相比第T[i]棵树，多插入了一个数字， 也就相当于修改了一条链。

如果第a[i+1]个数插入了T[i+1]的左子树， 那么T[i+1]的右子树和T[i]的右子树是一样的， 所以可以直接指向T[i]的右子树， 然后子树的构造也是这个道理。

poj2104

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <time.h>
using namespace std;
/*
可持久化线段树，函数式线段树，主席树
动态第k大

线段树维护的是值出现的次数
*/
const int N = ;
int a[N], t[N];
//T[i] 保存第i棵线段树的根
int T[N], lson[N * ], rson[N * ], c[N * ];
int n, m, q, tot;
int build(int l, int r)
{
    int root = tot++;
    c[root] = ;
    if (l != r)
    {
        int mid = (l + r) >> ;
        lson[root] = build(l, mid);
        rson[root] = build(mid + , r);
    }
    return root;
}

//root是第i棵线段树的根， 现在构造第i+1棵树， pos是a[i+1]所要插入的位置
int update(int root, int pos)
{
    int newRoot = tot++, tmp = newRoot;
    int l = , r = m;
    c[newRoot] = c[root] + ;
    while (l < r)
    {
        int mid = (l + r) >> ;
        if (pos <= mid)//要插入的位置位于左子树， 要么右子树可以指向第i棵线段树的右子树
        {
            r = mid;
            lson[newRoot] = tot++;
            rson[newRoot] = rson[root];
            newRoot = lson[newRoot];//继续构造左子树
            root = lson[root];
        }
        else
        {
            l = mid + ;
            lson[newRoot] = lson[root];
            rson[newRoot] = tot++;
            newRoot = rson[newRoot];
            root = rson[root];
        }
        c[newRoot] = c[root] + ;//该子树保存的值的个数+1
    }
    return tmp;
}

int hs(int x)
{
    return lower_bound(t + , t + m + , x) - t;
}

int query(int leftroot, int rightroot, int k)
{
    int l = , r = m;
    while (l < r)
    {
        int mid = (l + r) >> ;
        if (c[lson[rightroot]] - c[lson[leftroot]] >= k)
        {
            r = mid;
            rightroot = lson[rightroot];
            leftroot = lson[leftroot];
        }
        else
        {
            l = mid + ;
            k -= c[lson[rightroot]] - c[lson[leftroot]];
            rightroot = rson[rightroot];
            leftroot = rson[leftroot];

        }
    }
    return l;
}
int main()
{
    while (scanf("%d%d", &n, &q) != EOF)
    {
        tot = ;
        for (int i = ; i <= n; ++i)
        {
            scanf("%d", &a[i]);
            t[i] = a[i];
        }
        sort(t + , t + n + );
        m = unique(t + , t + n + ) - t - ;
        T[] = build(, m);
        for (int i = ; i <= n; ++i)
        {
            int pos = hs(a[i]);
            //第i棵线段树由第i-1棵线段树修改而来
            T[i] = update(T[i - ], pos);
        }
        while (q--)
        {
            int l, r, k;
            scanf("%d%d%d", &l, &r, &k);
            printf("%d\n", t[query(T[l - ], T[r], k)]);
        }

    }
    return ;
}