洛谷P2617 Dynamic Ranking（主席树，树套树，树状数组）

洛谷题目传送门

YCB巨佬对此题有详细的讲解。%YCB%请点这里

思路分析

不能套用静态主席树的方法了。因为的\(N\)个线段树相互纠缠，一旦改了一个点，整个主席树统统都要改一遍。。。。。。

话说我真的快要忘了有一种数据结构，能支持单点修改，区间查询，更重要的是，常数优秀的它专门用来高效维护前缀和！！它就是——

！树状数组！

之前静态主席树要保存的每个线段树\([1,i]\),不也是一个庞大的前缀吗？于是，把树状数组套在线段树上，构成支持动态修改的主席树。每个树状数组的节点即为一个线段树的根节点。

举个栗子，维护一个长度为\(5\)的序列，树状数组实际会长成这样——

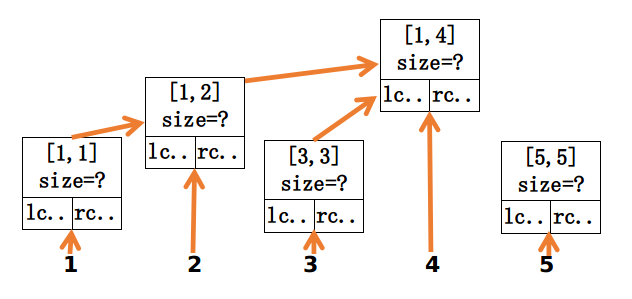
于是就利用树状数组来维护前缀和了。首先是修改（设修改元素位置为\(i\)）。从下标为\(i\)的树状数组节点开始，每次都往后跳（+=lowbit(i)），所有跳到的线段树都改一遍，原值对应区间-1，新值对应区间+1。一共要改\(log\)棵树。

然后是查询。先把\(l-1\)和\(r\)都往前跳（-=lowbit(i)），每次跳到的都记下来。求当前\(size\)的时候，用记下来的\(log\)棵由\(r\)得到的节点左儿子的\(size\)和（就代表\([1,r]\)的\(size\)）减去\(log\)棵由\(l-1\)得到的节点左儿子的\(size\)和（就代表\([1,l-1]\)的\(size\)）就是\([l,r]\)的\(size\)。往左/右儿子跳的时候也是\(log\)个节点一起跳。

其实还有一个问题，一开始本蒟蒻想不通，就是\(N\)棵线段树已经无法共用内存了，那空间复杂度不会是\(O(N^2\log N)\)吗？

其实没必要担心的。。。。。。

只考虑修改操作，每次有\(log\)棵线段树被挑出来，每个线段树只修改\(log\)个节点，因此程序一趟跑下来，仅有\(N\log^2N\)个节点被访问过，我们只需要动态开点就好了。

下面贴代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define R register int
const int N=10009,M=4000009;//M：开Nlog²的空间
bool op[N];
int L,P,n,a[N],b[N],c[N],d[N],g[N<<1];
int rt[N],lc[M],rc[M],s[M];
int pl,pr,reql[20],reqr[20];
#define G ch=getchar()
#define GO G;while(ch<'-')G
#define in(z) GO;z=ch&15;G;while(ch>'-')z*=10,z+=ch&15,G
inline void update(R p,R v)//修改
{
    R k=lower_bound(g+1,g+L+1,a[p])-g;//先找到离散化后对应值
    for(R i=p;i<=n;i+=i&-i)
    {
        R*t=&rt[i],l=1,r=L,m;
        while(l!=r)
        {
            if(!*t)*t=++P;//动态分配空间
            s[*t]+=v;
            m=(l+r)>>1;
            if(k<=m)r=m,t=&lc[*t];
            else  l=m+1,t=&rc[*t];
        }
        if(!*t)*t=++P;
        s[*t]+=v;
    }
}
inline int ask(R l,R r,R k)
{
    R i,m,sum;
    pl=pr=0;
    for(i=l-1;i;i-=i&-i)
        reql[++pl]=rt[i];
    for(i=r;i;i-=i&-i)
        reqr[++pr]=rt[i];//需要查询的log个线段树全记下来
    l=1;r=L;
    while(l!=r)
    {
        m=(l+r)>>1;sum=0;
        for(i=1;i<=pr;++i)sum+=s[lc[reqr[i]]];
        for(i=1;i<=pl;++i)sum-=s[lc[reql[i]]];//一起加一起减
        if(k<=sum)
        {
            for(i=1;i<=pl;++i)reql[i]=lc[reql[i]];
            for(i=1;i<=pr;++i)reqr[i]=lc[reqr[i]];
            r=m;
        }//一起向同一边儿子跳
        else
        {
            for(i=1;i<=pl;++i)reql[i]=rc[reql[i]];
            for(i=1;i<=pr;++i)reqr[i]=rc[reqr[i]];
            l=m+1;k-=sum;
        }
    }
    return g[l];
}
int main()
{
    register char ch;
    R m,i;
    in(n);in(m);L=n;
    for(i=1;i<=n;++i){in(a[i]);}
    memcpy(g,a,(n+1)<<2);
    for(i=1;i<=m;++i)
    {
        GO;op[i]=ch=='Q';
        in(b[i]);in(c[i]);
        if(op[i]){in(d[i]);}
        else g[++L]=c[i];//变成动态的了，离散化时后面需要修改的值也要考虑进去，所以先把所有操作保存起来
    }
    sort(g+1,g+L+1);
    L=unique(g+1,g+L+1)-g-1;//离散化
    for(i=1;i<=n;++i)update(i,1);//一开始还是每个点都要更新一遍
    for(i=1;i<=m;++i)
    {
        if(op[i])printf("%d\n",ask(b[i],c[i],d[i]));
        else
        {
            update(b[i],-1);//注意被替代的以前那个值要减掉
            a[b[i]]=c[i];
            update(b[i],1);
        }
    }
    return 0;
}