●ZOJ 2112 Dynamic Rankings

●赘述题目

对于一个长为n（n<50000）的序列（序列中的数小于1000000000），现有如下两种指令：

Q a b c：询问区间[a,b]中第c小的数。

C p b：将序列中的从左往右数第p个数改成b。

●题解

（整体二分应该可以做吧。。。但写不来了）

主席树+树状数组套线段树维护。

本题和POJ 2104 K-th Number相比，多了一个修改操作，但真的做得我心累。

看看POJ 2104 的查询函数：

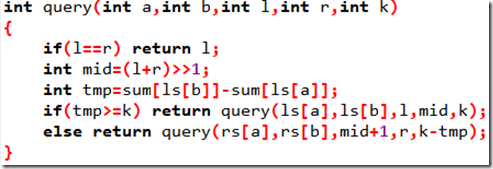
查询区间到底是往左还是往右，这决于tmp与k大小关系。但本题因为有修改操作，导致上图的sum[ ]存的信息不正确，无法正确二分下去。所以我们需要就修改操作进行信息的更新。

对于一个修改操作C p b，我们可以发现，这个操作会影响tr[p-n]这一堆主席树，那当然是不能直接枚举这一堆主席树，挨个进行修改，显然会超时。

于是便尝试再另外弄一个东西来单独维护修改后的信息。

不难发现，这一堆主席树，它们的修改操作是一模一样的，那便可以看作是一个区间修改，单点查询（如下图）呢，那我们就用树状数组来维护。

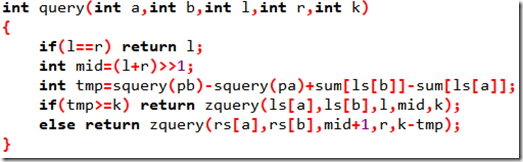
squery(x)是对树状数组的询问，表示序列区间[1-x]内有多少在[l-r]（权值）范围内的数发生了变化(少了则减，多了则加)。

举个例子，当原序列为 1 2 3 4 ，已经执行了修改操作C 2 5

若 l=1，r=4：squery(1)=0; squery(2)=-1; squery(3)=-1; squery(4)=-1;

若 l=5，r=8 : squery(1)=0; squery(2)=1; squery(3)=1; squery(4)=1;

若 l=1，r=8 : squery(1)=0; squery(2)=0; squery(3)=0; squery(4)=0;

（一定要弄懂哦。）

另外，树状数组该如何维护在[l-r]范围内的数发生的变化呢，那就树套树呗（以前从未写过树套树。。。），对于每个树状数组的节点建一颗权值线段树。

○至此，便有了一个大致的修改操作的思路：

对于C p b ，

先是枚举树状数组的节点（数组数组区间修改（单点查询），不用多说了吧）

for(int i=p;i<=n;i+=lowbit(i)) xmodify( ) ，对枚举到的节点里套的权值线段树进行单点修改。

到时候查询树状数组的时候，就for(int i=p;i>0;i-=lowbit(i)) ret+=xquery( )，对每个枚举到的节点里套的权值线段树进行权值区间查询并累加就好了。

（注意：若每个树状数组节点里都套的是一棵完整的权值线段树，空间必然不够，但因为修改数不超过10000，每次修改都只修改log n条链，这意味着我们需要用到的权值线段树的某些位置，在修改时临时建就好了，最后每个树状数组节点里都套的都是我们想象的完整的权值线段树，实际上只是几条链，甚至一条链没有。）

那么，完了吗？

我们算一算： m个操作，每个操作有一个log级别的主席树查询，再有一个 log级别的树状数组查询， 再套一个log级别的权值线段树查询，总的是复杂度是mlogloglog，可能要超时呢。

看看别的大佬的做法，每次主席树查询到[l-r]区间时，我们查询的每个权值线段树区间也是[l-r]（且该区间是直接二分得到的，而不是几个小区间拼凑而来），那便可以先用一个数组存下要用的权值线段树的节点，当询问树状数组时由储存的权值线段树的节点直接获取权值区间信息便是了。这样是一个 mloglog的复杂度。

所以，这里生长着两棵树，一颗是主席树（保存初始信息），一颗是套了线段树的树状数组（维护修改信息）。那么，本题也就结束了。

好吧，其实还有漫长的调试查错呢！

●代码

先大致解释一下函数名：（XX表示原函数名，如build,modify,squery。。。）

zXX表示关于主席树的函数；

sXX表示关于树状数组的函数；

xXX表示关于线段树的函数；

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
const int MAXN = 60010;
const int M = 2500010;
using namespace std;
int sum[M],ls[M],rs[M];
int xx[MAXN],aa[MAXN],tr[MAXN],s[MAXN],use[MAXN];
int tot=0,cnt,n,m,pa,pb;
struct operation{
	char ch;int a,b,c;
}op[10005];
int discrete(int x){return lower_bound(xx+1,xx+cnt+1,x)-xx;}
void xmodify(int &u,int l,int r,int x,int d)
{
	if(!u) u=++tot,sum[u]=0;
	sum[u]+=d;
	if(l==r){return;}
	int mid=(l+r)>>1;
	if(x<=mid) xmodify(ls[u],l,mid,x,d);
	else xmodify(rs[u],mid+1,r,x,d);
}
int lowbit(int x) {return x&-x;}
void smodify(int p,int x,int d)
{
	for(int i=p;i<=n;i+=lowbit(i)) xmodify(s[i],1,cnt,x,d);
}
int squery(int x)
{
	int ret=0;
	for(int i=x;i>0;i-=lowbit(i)) ret+=sum[ls[use[i]]];
	return ret;
}
void zbuild(int &u,int l,int r)
{
	u=++tot; sum[u]=0;
	if(l==r) return;
	int mid=(l+r)>>1;
	zbuild(ls[u],l,mid);
	zbuild(rs[u],mid+1,r);
}
void zupdate(int &u,int last,int l,int r,int p)
{
	u=++tot; sum[u]=sum[last]+1;
	if(l==r) return;
	ls[u]=ls[last]; rs[u]=rs[last];
	int mid=(l+r)>>1;
	if(p<=mid) zupdate(ls[u],ls[last],l,mid,p);
	else zupdate(rs[u],rs[last],mid+1,r,p);
}
int zquery(int a,int b,int l,int r,int k)
{
	if(l==r) return l;
	int mid=(l+r)>>1;
	int tmp=squery(pb)-squery(pa)+sum[ls[b]]-sum[ls[a]];
	if(tmp>=k)
	{
		for(int i=pa;i>0;i-=lowbit(i)) use[i]=ls[use[i]];
		for(int i=pb;i>0;i-=lowbit(i)) use[i]=ls[use[i]];
		return zquery(ls[a],ls[b],l,mid,k);
	}
	else
	{
		for(int i=pa;i>0;i-=lowbit(i)) use[i]=rs[use[i]];
		for(int i=pb;i>0;i-=lowbit(i)) use[i]=rs[use[i]];
		return zquery(rs[a],rs[b],mid+1,r,k-tmp);
	}
}
int main()
{
	int ans,dd,T;
	scanf("%d",&T);
	while(T--)
	{
		tot=cnt=dd=0;
		scanf("%d%d",&n,&m);
		memset(s,0,sizeof(s));
		memset(ls,0,sizeof(ls));
		memset(rs,0,sizeof(rs));
		for(int i=1;i<=n;i++) scanf("%d",&aa[i]),xx[++dd]=aa[i];
		for(int i=1;i<=m;i++)
		{
			scanf(" %c",&op[i].ch);
			if(op[i].ch=='Q') scanf("%d%d%d",&op[i].a,&op[i].b,&op[i].c);
			else scanf("%d%d",&op[i].a,&op[i].b),xx[++dd]=op[i].b;
		}
		sort(xx+1,xx+dd+1);
		cnt=unique(xx+1,xx+dd+1)-xx-1;
		zbuild(tr[0],1,cnt);
		for(int i=1;i<=n;i++)
		{
			int p=discrete(aa[i]);
			zupdate(tr[i],tr[i-1],1,cnt,p);
		}
		for(int i=1,a,b,k;i<=m;i++)
		{
			a=op[i].a; b=op[i].b;
			if(op[i].ch=='Q')
			{
				k=op[i].c;
				pa=a-1; pb=b;
				for(int j=pa;j>0;j-=lowbit(j)) use[j]=s[j];
				for(int j=pb;j>0;j-=lowbit(j)) use[j]=s[j];
				ans=zquery(tr[a-1],tr[b],1,cnt,k);
				printf("%d\n",xx[ans]);
			}
			else
			{
				int x=discrete(aa[a]),y=discrete(b);
				smodify(a,x,-1); smodify(a,y,1);
				aa[a]=b;
			}
		}
	}
	return 0;
}