视觉SLAM：滑动窗口

1.SLAM问题

1.1建模

考虑某个状态 \(\xi\),以及一次与该变量相关的观测 \(r_{i}\)。由于噪声存在，观测服从概率分布 \(p(r_{i}|\xi)\)。多个观测时，各个测量值相互独立，则多个测量 \(r = (r_{1}, ..., r_{n})^{T}\)构成的似然概率为：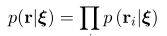

如果知道机器人状态的先验信息 \(p(\xi)\)，如GPS,码盘信息等，则由贝叶斯法则，有后验概率：



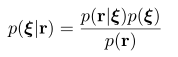
通过最大后验估计，获得系统状态的最优估计：



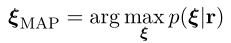
意为在当前的观测下，什么样的系统状态出现的概率最大。

分母跟状态量无关，舍弃取log。即：



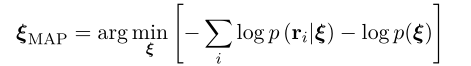
如果观测服从多元高斯分布：



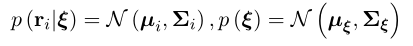
则有：

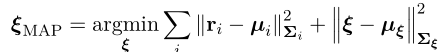
该问题可由最小二乘求解：

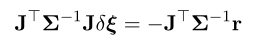
零均值的多元高斯分布概率为：\(p(x) = \frac{1}{Z}exp(-\frac{1}{2}x^{T}\Sigma^{-1}x)\)

其中\(\Sigma\)是协方差矩阵。\(\Sigma^{-1}\)为协方差矩阵的逆，即信息矩阵。

2.边缘化信息矩阵

使用滑动窗口不可避免的要移除掉变量，当移除变量的时候，之前与之不相关的变量，有可能变得相关，所以要对信息矩阵进行维护。

这里使用舒尔补来对信息矩阵进行边缘化处理。

2.1舒尔补的定义：

给定任意的矩阵块M，如下所示：



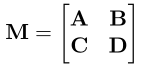
如果，矩阵块D是可逆的，则 \(A-BD^{-1}C\)称之为D关于M的舒尔补

如果。矩阵块A是可你的，则 \(D-CA^{-1}B\)称之为A关于M的舒尔补

2.2使用舒尔补来去除变量：

假如一个系统三个变量x1,x2,x3。其信息矩阵为：



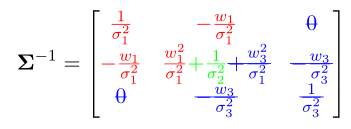
那么把x3去掉，也就是把蓝色部分去掉，利用舒尔补。



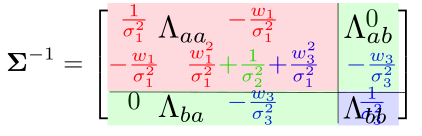
则去掉后的信息矩阵为：

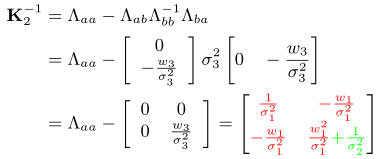
3.滑动窗口算法

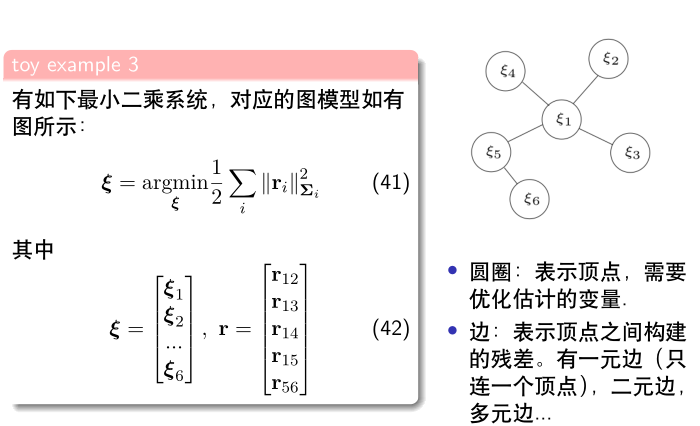
上述最小二乘问题，对应的高斯牛顿求解为：



注意：这里的H反应的是求解的方差，而\(\Sigma^{-1}\)反应的是残差的方差

公式中的雅可比矩阵为：



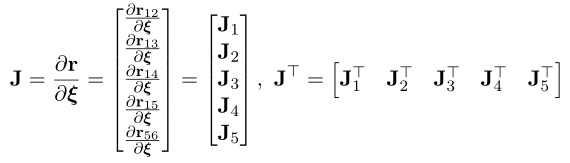
矩阵乘法公式可以写成连加：

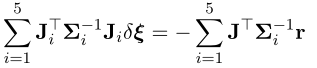
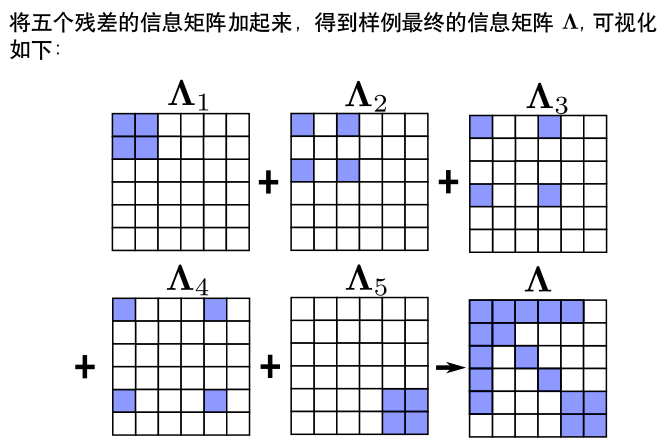
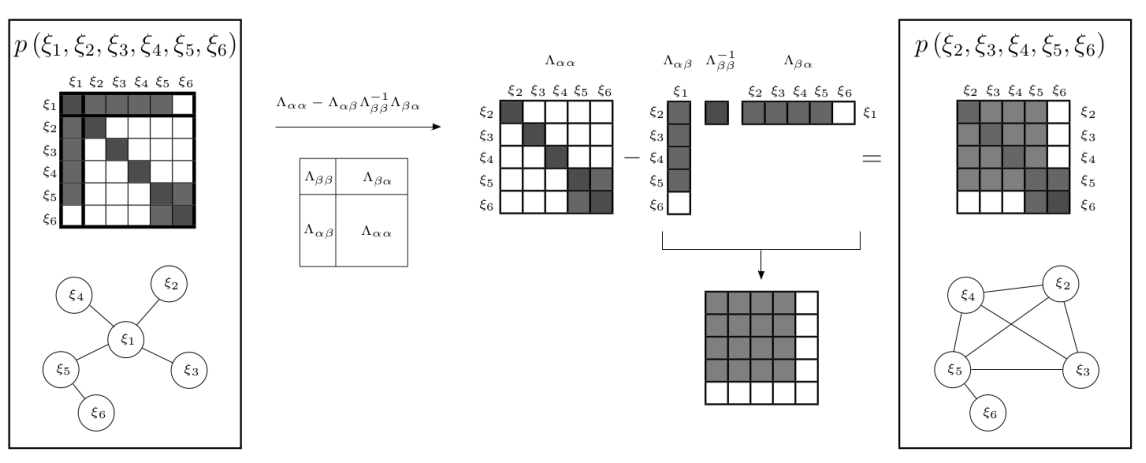
使用边际概率移除变量\(\xi_{1}\),信息矩阵的变化过程：