模拟赛：树和森林(lct.cpp) （树形DP，换根DP好题）

题面

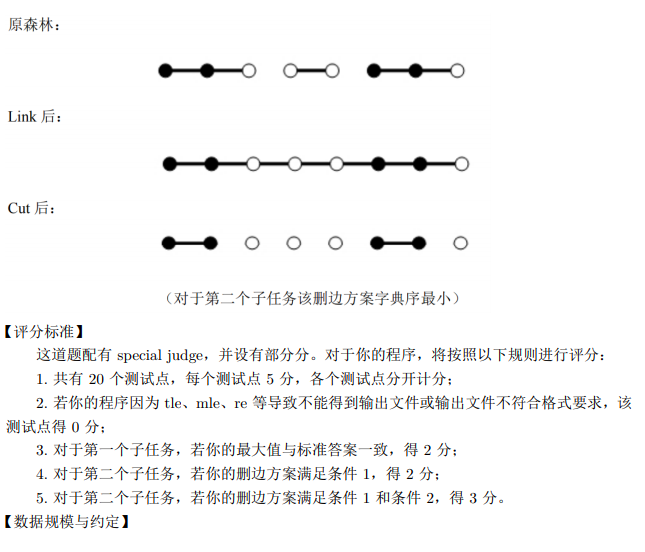
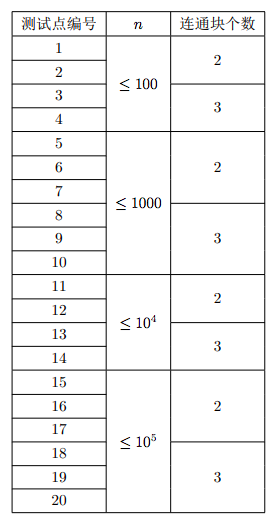
题解

先解决第一个子问题吧，它才是难点

Subtask_1

我们可以先用一个简单的树形DP处理出每棵树内部的dis和，记为dp0[i]，

然后再用一个换根的树形DP处理出每棵树内点 i 到树内每个点的距离和，记为dp[i]，

好，现在分两个连通块跟三个连通块两种情况讨论

两个连通块

把两棵树A，B合并到一起，我们得先确定两个连接的点，

若其分别为 i，j，不难发现答案就是 dp0[A] + dp0[B] + dp[i] * size[B] + dp[j] * size[A] + size[A] * size[B]

其中，dp0[A]，dp0[B]，size[A]，size[B]都是确定的，那么当答案取最大的时候，dp[i]、dp[j]一定分别都取最大

所以在两棵树中找dp值最大的两个点 i , j 就行了。

三个连通块

两条边连接三棵树，幸运的是，大的情况只有三种（A-B-C , A-C-B , B-A-C）

其中一棵树一定连了两条边，且不一定是同一个点连出去，不妨设中间那棵为B

注意到中间那条绿色的路径没？也就是说中间是可能有两个点的

若连接的两个点分别为 i，j，那么仔细开动一下脑筋，会发现总的贡献是

其中随着 i，j 变化的只有  

因此，若以B树上每个节点为 i 考虑，我们可以用一个简单的换根DP求出上式的最大值，记为dp2[i]，然后再求出B树中最大的dp2[i]，加到上面三排的式子中，答案就出来了。

Subtask_2

子问题二其实更简单，不用管它的第二个条件，因为它只有0~1个解。

原图是个森林，是很多树组成，所以先考虑叶子结点，叶子结点如果是黑的，它的父边就不能删，如果是白的，它的父边就必须删；然后消除它父边的影响，再把叶子删去。这样一来，又有新的叶子，重复考虑……可以发现，最后要么无解，要么只有一个解，而且很好输出。

CODE

#include<map>
#include<queue>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 100005
#define LL unsigned long long
#define DB double
#define ENDL putchar('\n')
#define lowbit(x) ((-x)&(x))
LL read() {
    LL f = 1,x = 0;char s = getchar();
    while(s < '0' || s > '9') {if(s=='-')f=-f;s = getchar();}
    while(s >= '0' && s <= '9') {x=x*10+(s-'0');s=getchar();}
    return f*x;
}
const int MOD = 998244353;
int n,m,i,j,s,o,k;
vector<int> g[MAXN];
vector<int> id[MAXN];
char cl[MAXN];
int U[MAXN],V[MAXN];
int siz[MAXN],rt[10],cnt;
LL dp1[MAXN],dp2[MAXN],ma[MAXN],sm[MAXN],dp[MAXN];
LL dpu[MAXN],dpd[MAXN],dpa[MAXN];
vector<LL> pre[MAXN],suf[MAXN];
bool vis[MAXN],f[MAXN],ad[MAXN];
void dfs1(int x,int fa) {
	vis[x] = 1;
	siz[x] = 1;
	dp1[x] = 0;
	for(int i = 0;i < g[x].size();i ++) {
		int y = g[x][i];
		if(y != fa) {
			dfs1(y,x);
			siz[x] += siz[y];
			dp1[x] += dp1[y] + (LL)siz[y];
		}
	}return ;
}
void dfs2(int x,int fa,int n) {
	dp2[x] = 0;
	if(fa) {
		dp2[x] = (dp2[fa] + (dp1[fa] - (dp1[x] + (LL)siz[x]))) + (n-siz[x]);
	}
	dp[x] = dp1[x] + dp2[x];
	ma[x] = dp[x];
	sm[x] = siz[x] * (n-siz[x]);
	for(int i = 0;i < g[x].size();i ++) {
		int y = g[x][i];
		if(y != fa) {
			dfs2(y,x,n);
			ma[x] = max(ma[x],ma[y]);
			sm[x] += sm[y];
		}
	}
	return ;
}
void dfs3(int x,int fa,int sizA,int sizB) {
	dpd[x] = dp[x] * (LL)sizB + sizA *2ll* sizB;
	LL pr = 0;
	for(int i = 0;i < g[x].size();i ++) {
		pre[x].push_back(pr);
		int y = g[x][i];
		if(y != fa) {
			dfs3(y,x,sizA,sizB);
			pr = max(pr,dpd[y] + sizA *1ll* sizB);
			dpd[x] = max(dpd[x],dpd[y] + sizA *1ll* sizB);
		}
	}
	pr = 0;
	for(int i = (int)g[x].size()-1;i >= 0;i --) {
		suf[x].push_back(pr);
		int y = g[x][i];
		if(y != fa) {
			pr = max(pr,dpd[y] + sizA *1ll* sizB);
		}
	}
	return ;
}
void dfs4(int x,int fa,int sizA,int sizB,int ad1,int ad2) {
	dpu[x] = dp[x] * (LL)sizB + sizA *2ll* sizB;
	if(fa) {
		dpu[x] = max(dpu[x],max(dpu[fa],max(pre[fa][ad1],suf[fa][ad2])) + sizA *1ll* sizB);
	}
	dpa[x] = max(dpd[x],dpu[x]) + dp[x] * (LL)sizA;
	for(int i = 0;i < g[x].size();i ++) {
		int y = g[x][i];
		if(y != fa) {
			dfs4(y,x,sizA,sizB,i,(int)g[x].size()-1-i);
			dpa[x] = max(dpa[x],dpa[y]);
		}
	}return ;
}
bool dfs5(int x,int fa,int ed) {
	for(int i = 0;i < g[x].size();i ++) {
		int y = g[x][i],idn = id[x][i];
		if(y != fa) {
			bool cg = dfs5(y,x,idn);
			f[x] ^= cg;
		}
	}
	if(f[x]) ad[ed] = 1;
	return f[x];
}
int main() {
//	freopen("lct.in","r",stdin);
//	freopen("lct.out","w",stdout);
	n = read();m = read();
	scanf("%s",cl + 1);
	for(int i = 1;i <= m;i ++) {
		s = read();o = read();
		U[i] = s;V[i] = o;
		g[s].push_back(o);
		g[o].push_back(s);
		id[s].push_back(i);
		id[o].push_back(i);
	}
	for(int i = 1;i <= n;i ++) {
		if(!vis[i]) {
			dfs1(i,0);
			dfs2(i,0,siz[i]);
			rt[++ cnt] = i;
		}
	}
	LL ans1 = 0;
	if(cnt == 2) {
		ans1 = ma[rt[1]] * siz[rt[2]] + ma[rt[2]] * siz[rt[1]] + siz[rt[2]] *1ll* siz[rt[1]];
		ans1 += sm[rt[1]] + sm[rt[2]];
	}
	else if(cnt == 3) {
		LL DP1 = ma[rt[1]] * (LL)(n-siz[rt[1]]),D1 = siz[rt[1]] *1ll* (n-siz[rt[1]]);
		LL DP2 = ma[rt[2]] * (LL)(n-siz[rt[2]]),D2 = siz[rt[2]] *1ll* (n-siz[rt[2]]);
		LL DP3 = ma[rt[3]] * (LL)(n-siz[rt[3]]),D3 = siz[rt[3]] *1ll* (n-siz[rt[3]]);
		dfs3(rt[1],0,siz[rt[2]],siz[rt[3]]);
		dfs4(rt[1],0,siz[rt[2]],siz[rt[3]],0,0);
		ans1 = max(ans1,dpa[rt[1]] + DP2 + DP3 + D1);

		dfs3(rt[2],0,siz[rt[1]],siz[rt[3]]);
		dfs4(rt[2],0,siz[rt[1]],siz[rt[3]],0,0);
		ans1 = max(ans1,dpa[rt[2]] + DP1 + DP3 + D2);

		dfs3(rt[3],0,siz[rt[1]],siz[rt[2]]);
		dfs4(rt[3],0,siz[rt[1]],siz[rt[2]],0,0);
		ans1 = max(ans1,dpa[rt[3]] + DP1 + DP2 + D3);

		ans1 += sm[rt[1]] + sm[rt[2]] + sm[rt[3]];
	}
	printf("%lld\n",ans1);
	for(int i = 1;i <= n;i ++) f[i] = (cl[i] == 'B' ? 1:0);
	bool flag = 0;
	for(int i = 1;i <= cnt;i ++) {
		flag |= dfs5(rt[i],0,0);
	}
	if(flag) {
		printf("-1\n");
	}
	else {
		int cn = 0;
		for(int i = 1;i <= m;i ++) {
			if(ad[i]) cn ++;
		}
		printf("%d\n",cn);
		for(int i = 1;i <= m;i ++) {
			if(ad[i]) printf("%d ",i);
		}
		ENDL;
	}
    return 0;
}