图解 Andrew 算法求凸包

前言

Andrew 算法可以在 \(O(n\log n)\) 的时间复杂度通过单调栈分别求出散点的上凸壳和下凸壳，来求出平面上一些点的凸包。

看懂这篇博客，大家需要掌握：

• 基础计算几何知识
• 单调栈

凸包

首先，什么是凸包？

给你平面上的点集，你需要从中选出最少的点，使得这些点所组成的 凸多边形 可以包裹住其他所有点。这些点所组成的凸多边形就是凸包。

譬如下面这个点集：

它的凸包是：

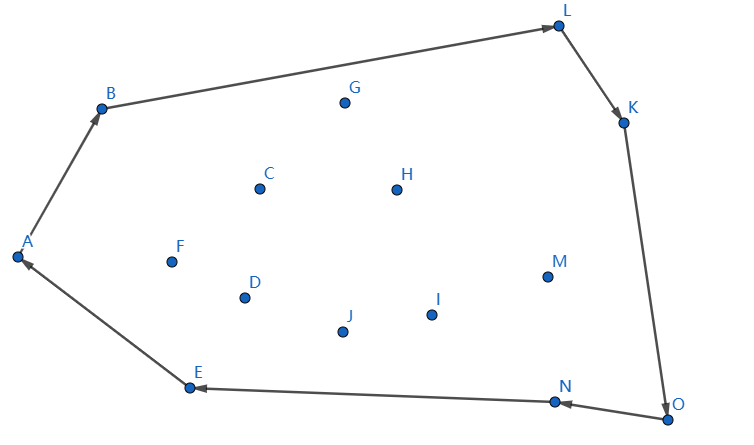
下面我将会告诉大家怎么求。

序曲

Andrew 算法需要先对所有点按照 \(x\) 坐标为第一关键字、\(y\) 坐标为第二关键字排序。如上面的点集，经过排序后是：

ABFEDCGJHILMNKO

那么 \(A\) 和 \(O\) 一定在凸包上，因为它们无法被其他点所组成的凸多边形覆盖。

按照 Andrew 算法的逻辑，我们需要先求出凸包的一半 “凸壳”。下面将会以上凸壳为例，下凸壳与其类似。

一段上凸壳一定满足顺时针遍历时，每个节点在每条边所组成的向量的右边（下凸壳在左边）（就是凸包的“凸”，下同）。这句话大家可能不能完全理解，不过没有关系，我会给大家慢慢道来。

流程

首先，按照排序后的点集遍历点集，第一个遍历到的是 \(B\)（\(A\) 不考虑）。我们可以连接 \(AB\)：

然后下一个点是 \(F\)，继续连接 \(BF\)：

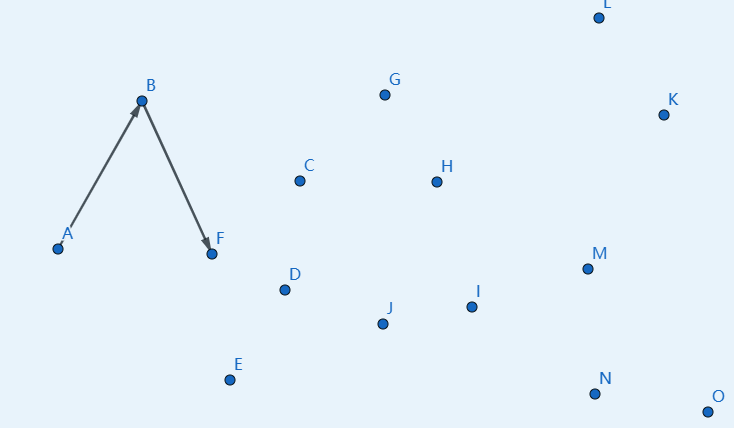
下一个点是 \(E\)，继续连接 \(FE\)：

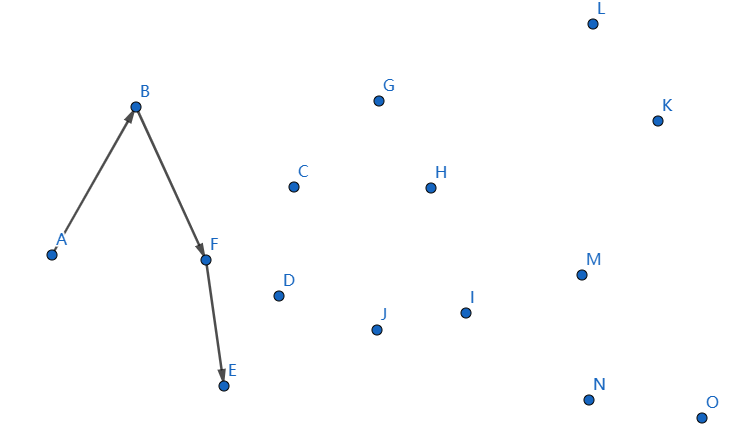
下一个点是 \(D\)，继续连接 \(ED\)：

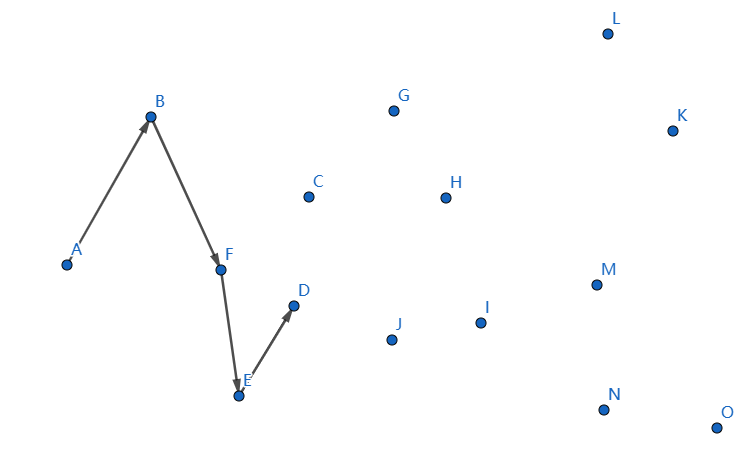
但是这样子我们遇到了问题，\(D\) 在 \(FE\) 左侧，它不凸了，我们的解决办法是：

断掉以前连的边，直到遇到可以连接的点，满足凸壳性质

我们可以断掉 \(ED,FE\)，连接 \(FD\)，发现还是不满足。

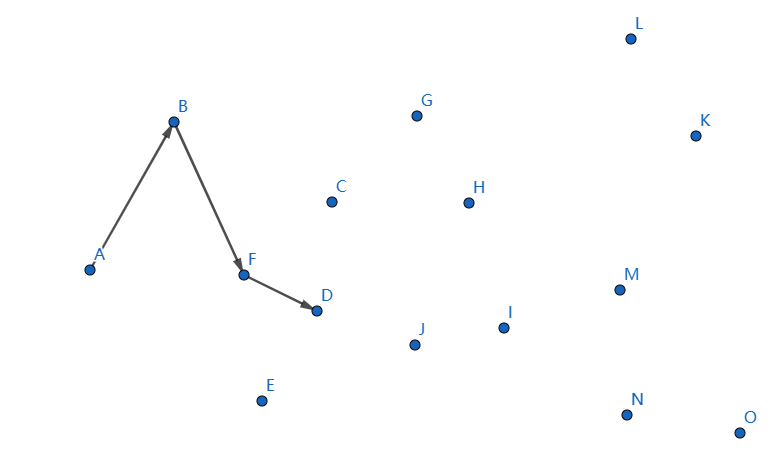
我们继续，断掉 \(FD,BF\)，连接 \(BD\)，这回满足了。

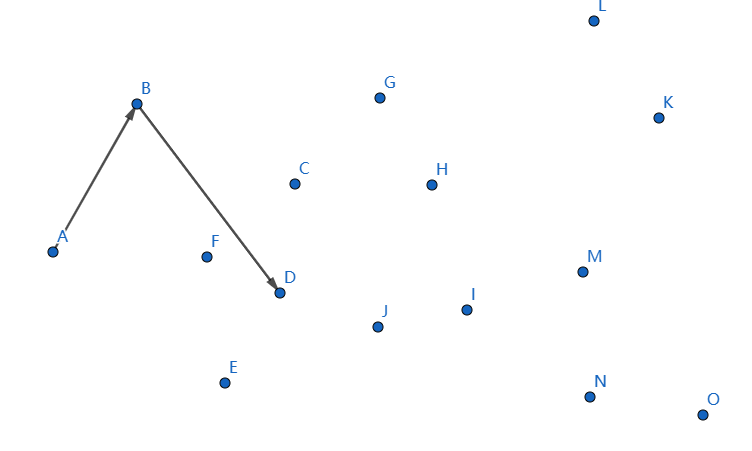
下一个点是 \(C\)，继续连接 \(DC\)：

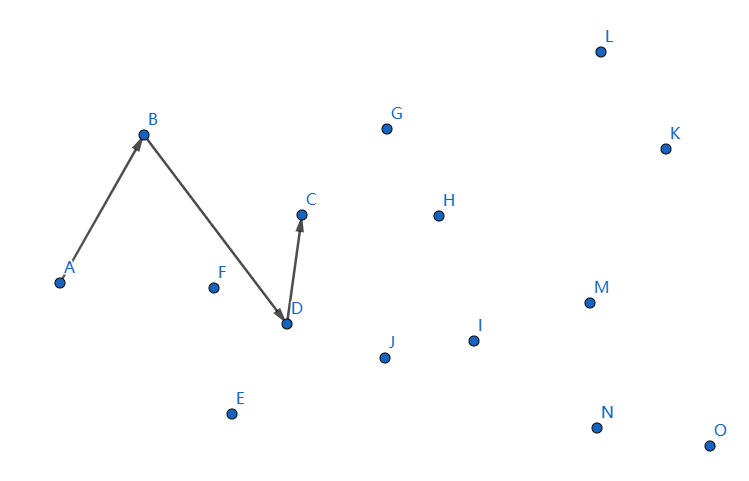
发现又不凸了，我们断掉 \(DC,BD\) 连接 \(BC\)，就可以满足了：

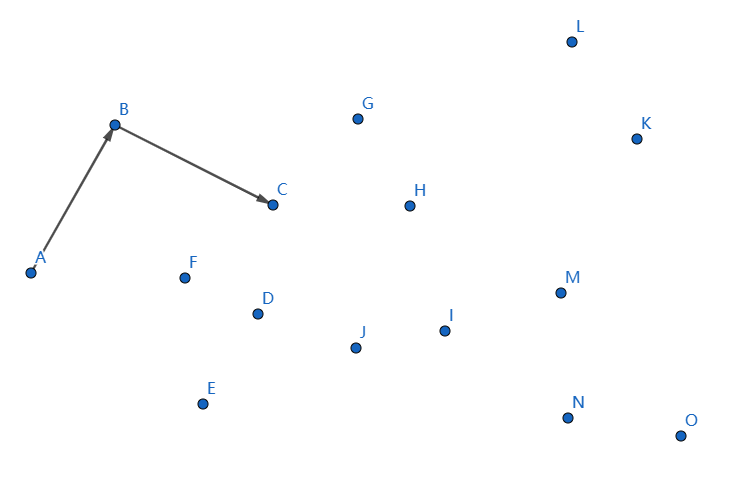
下一个点是 \(G\)，继续连接 \(CG\):

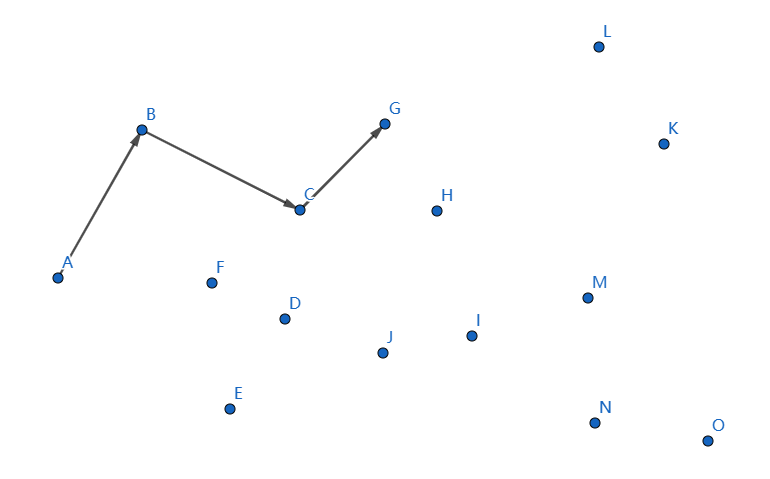
发现不凸，我们断掉 \(CG,BC\)，连接 \(BG\)：

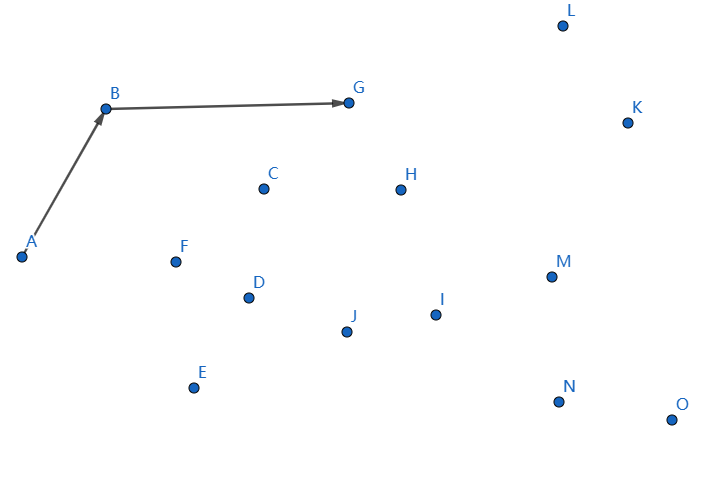
下一个点是 \(J\)，继续连接 \(GJ\):

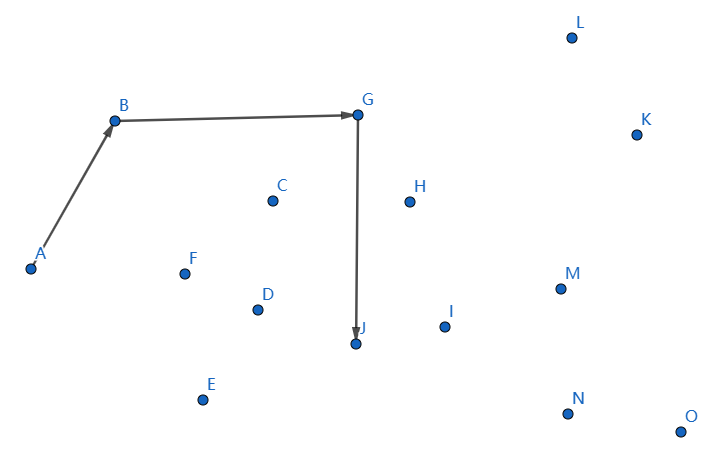
下一个点是 \(H\)，继续连接 \(JH\):

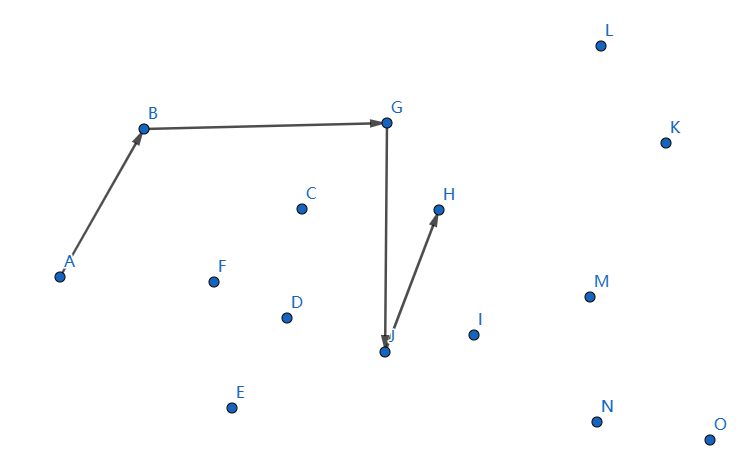
发现不凸，我们断掉 \(GJ,JH\)，连接 \(GH\)：

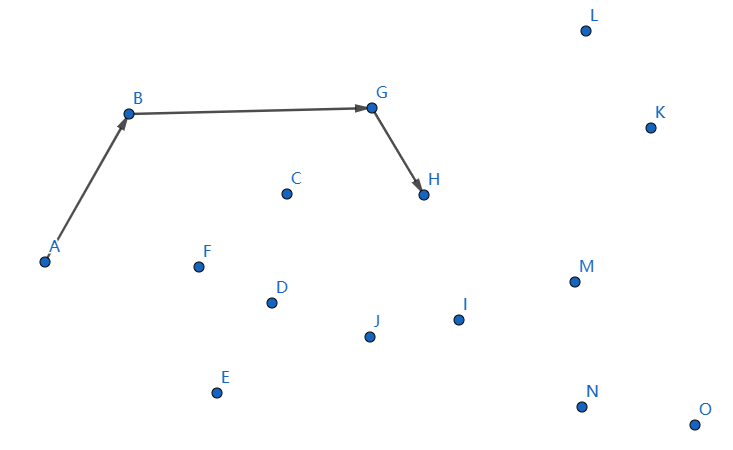
下一个点是 \(I\)，继续连接 \(HI\):

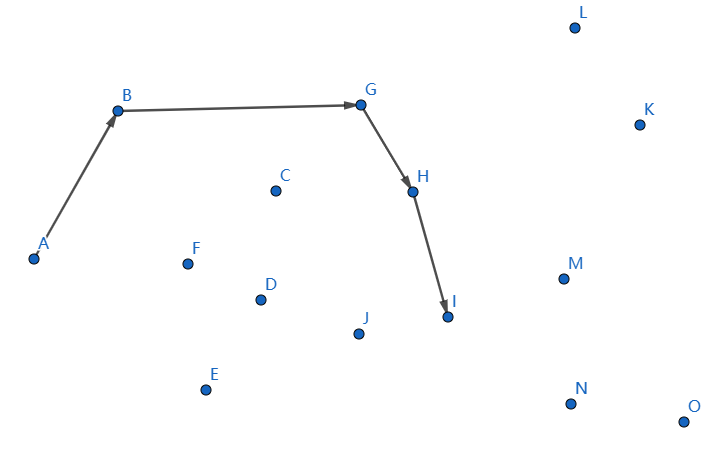
下一个点是 \(L\)，继续连接 \(IL\):

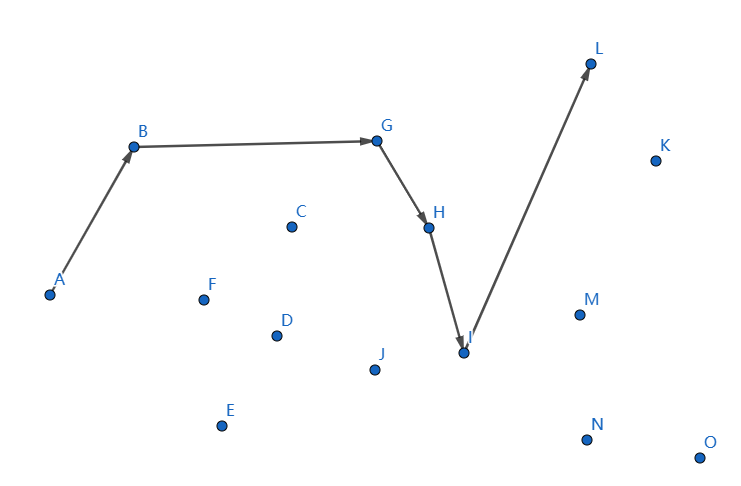
发现不凸，我们断掉 \(IL,HI\)，连接 \(HL\)：

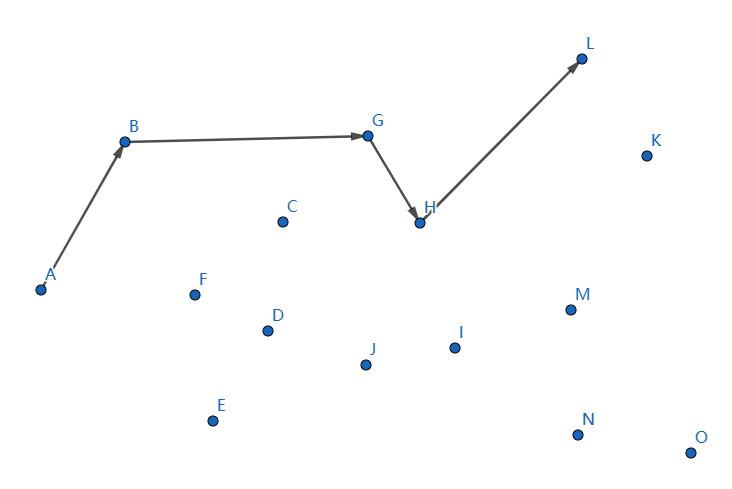
发现不凸，我们断掉 \(HL，GH\)，连接 \(GL\)：

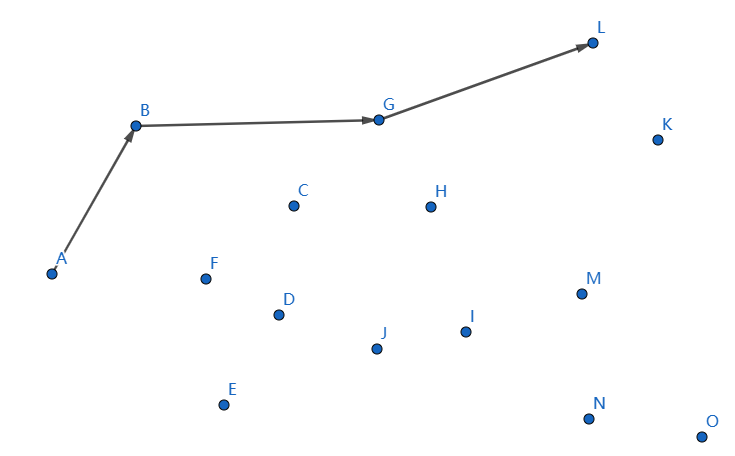
发现不凸，我们断掉 \(GL，BG\)，连接 \(BL\)：

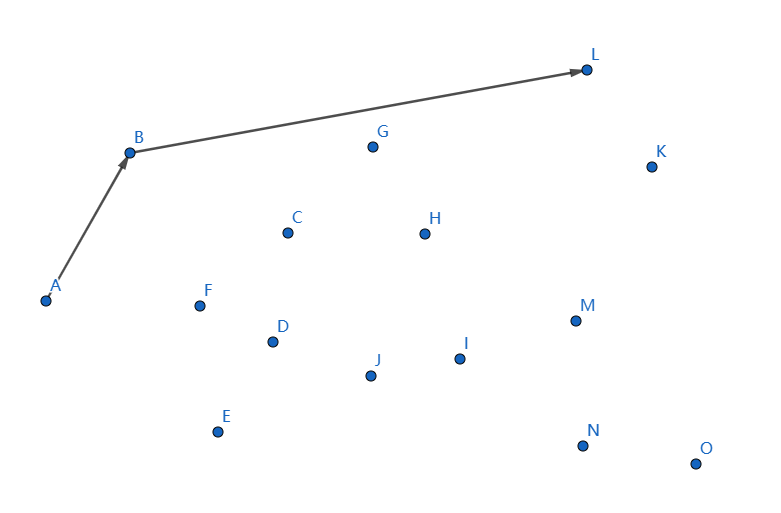
下一个点是 \(M\)，继续连接 \(LM\):

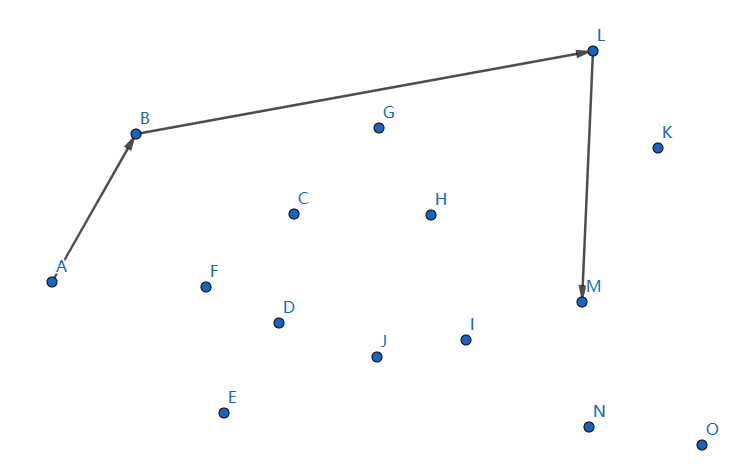
下一个点是 \(N\)，继续连接 \(MN\):

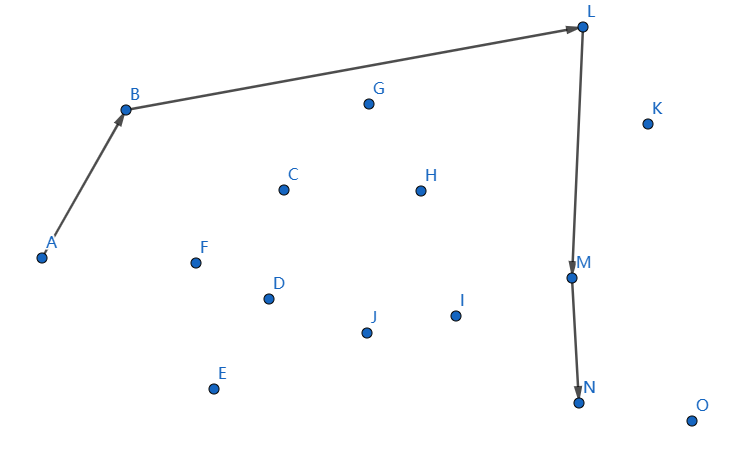
发现不凸，我们断掉 \(MN，LM\)，连接 \(LN\)：

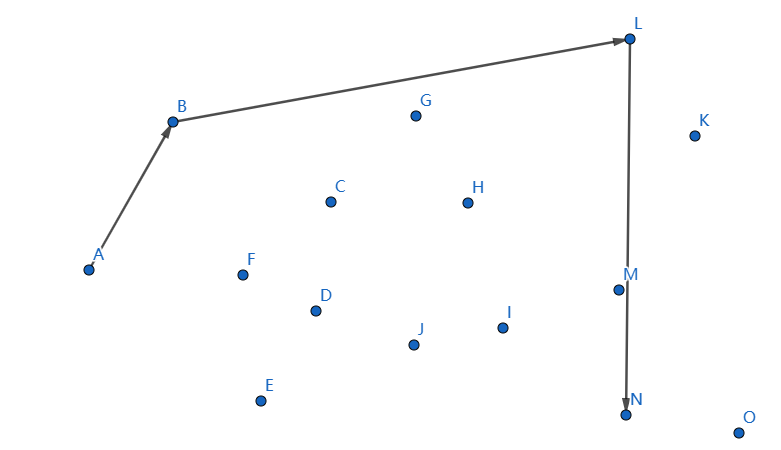
下一个点是 \(K\)，继续连接 \(NK\):

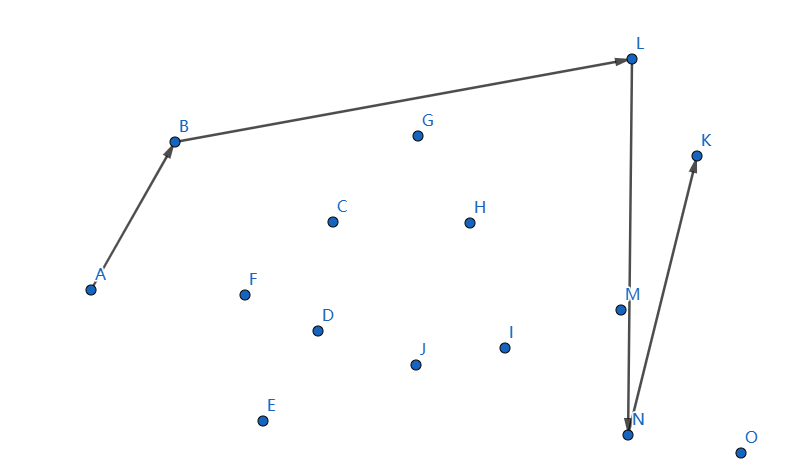
发现不凸，我们断掉 \(LN，NK\)，连接 \(LK\)：

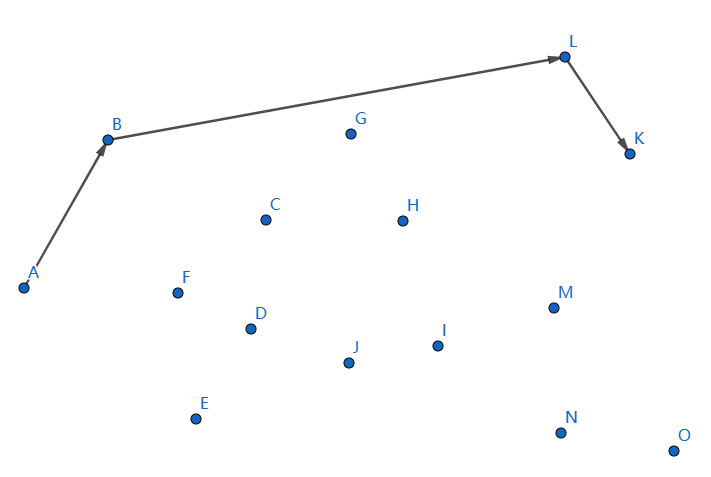
最后一个点是 \(O\)，我们连接 \(KO\)：

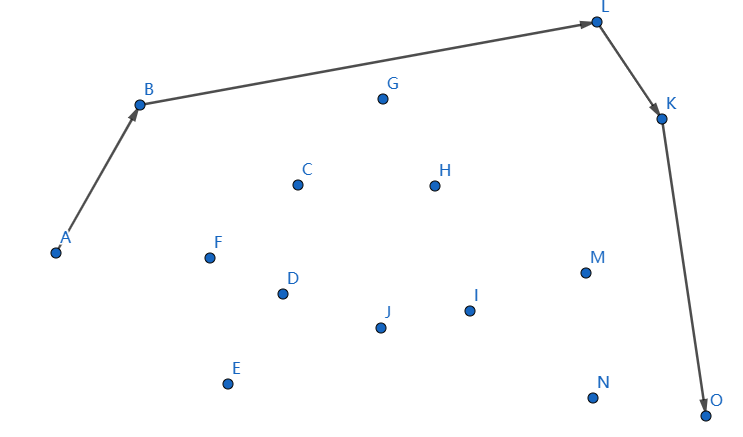
这样子上凸壳便求出来，下凸壳我们一般从 \(O\) 遍历到 \(A\)，按照以前的逻辑做即可，最后结果如下：

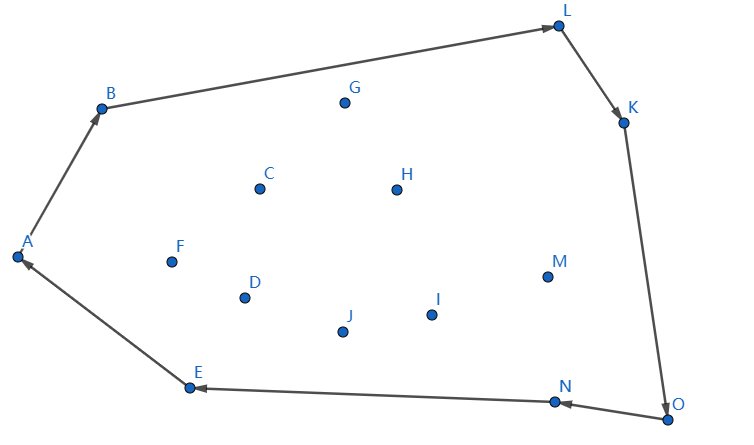
实现

维护“不凸就断边”我们使用单调栈，如果不满足凸的性质就弹栈，最后入栈即可。注意我们不需要模拟断边操作，只需要将点删除即可。

还有，如何判断是否在左边呢？我们可以使用叉乘的右手定则：

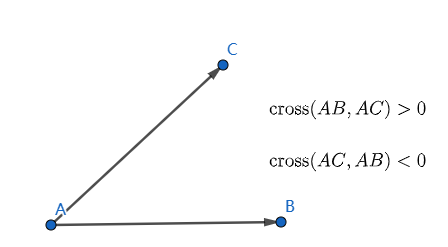
参考代码如下：

int stk[100005];
bool used[100005];
vector<Point> ConvexHull(Point* poly, int n){ // Andrew算法求凸包
    int top=0;
    sort(poly+1,poly+n+1,[&](Point x,Point y){
        return (x.x==y.x)?(x.y<y.y):(x.x<y.x);
    });
    stk[++top]=1;
    for(int i=2;i<=n;i++){
        while(top>1&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
            used[stk[top--]]=0;
        }
        used[i]=1;
        stk[++top]=i;
    }
    int tmp=top;
    for(int i=n-1;i;i--){
        if(used[i]) continue;
        while(top>tmp&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
            used[stk[top--]]=0;
        }
        used[i]=1;
        stk[++top]=i;
    }
    vector<Point> a;
    for(int i=1;i<=top;i++){
        a.push_back(poly[stk[i]]);
    }
    return a;
}

课后习题

• P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包
• P3829 [SHOI2012]信用卡凸包