stixel上边缘

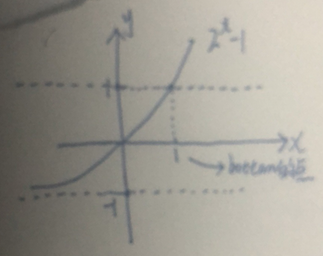
上图是2^x-1的曲线，取值范围在（-1，正无穷）

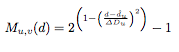
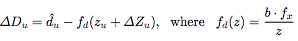
上面两个公式组成了隶属函数(membership)表示隶属度，隶属度就是衡量这个点同下边缘点是否属于同一个物体。实际上M函数就是2^x-1，但M函数的取值范围在(-1,1]，且bottom点取到最大值1.小于0的点属于背景，大于0的点属于物体。

1.为什么是(-1,1]且在bottom点最大？

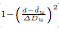首先2^x-1的取值范围是(-1，正无穷),那就看x的取值范围，x的取值范围是(负无穷,1).为什么是(负无穷,1)？ 的最小值是0，最大值是正无穷，所以 是(负无穷,1)。

2.为什么要除以delta(Du)？

当d-du的差值大于了delta(Du) ，整个 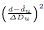 大于1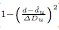， 也就小于0，同理当d-du的差值小于了delta(Du), 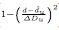大于0，当d =  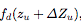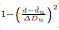， 等于0。

当d越小，d-du的差值也就越大(绝对值)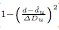， 也就更接近-1，由深度与disparity关系公式 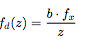得，d越小，深度z就越大，离物体也就越远，越远的话就越可能是背景。

除以delta(Du)就有了一个衡量disparity的隶属度的程度，也就是说假定depth在5米以内为物体的概率高，depth大于5米以外的概率小。为什么这么说？因为在后面的cost函数中，相当于是负值减去正值，最后的cost越小就越可能是上边缘点。通过delta(Du)，大于5米外的都是负值，小于5米内的都是正值

3.为什么用平方？

平方的话，可以放大差异，让大的值更大。

4.小于0不一定属于背景，大于0也不一定属于物体！

比如从上到下依次是(-0.5,0,0.1,-0.3,0.2,0)，用cost算出来是-0.3是上边缘点

为什么要用cost函数来求上边缘点？直接用membership为0的点不就好了吗？

首先membership为0的点，可能有很多。

为什么不直接弄成depth的陡变，而要转换为隶属度函数？

其实是把depth转换成概率问题

转化成隶属度问题，隶属度变化最大就为上边缘点，其实不是depth的陡变，而是以depth来衡量隶属度的概率，然后转化为求隶属度变化最大。那为什么要加上上面所有的值？

隶属度函数相当于把概率锁定在了-1，1

通过隶属度函数衡量点是否属于物体(越靠近下边缘点，隶属度越高)，然后通过cost代价函数找到边缘点(每个像素点所有的上部的隶属度减去下部的隶属度，说白了就是求一个整体的隶属度变化，然后获得极小值。其实可以发现，越往上走，隶属度负的越多，因为depth越大，disparity越小，那个隶属函数是判断与bottom点的差值，越往上越大)，然后通过动态规划找到上边缘曲线，同时如果两个bin之间有阶跃，会有惩罚函数。