Machine Learning笔记整理 ------ （四）线性模型

1. 线性模型

基本形式：给定由d个属性描述的样本 x = (x₁; x₂; ......; x_d)，其中，x_i是x在第i个属性上的取值，则有：

f(x) = w₁x₁ + w₂x₂ + ...... + w_dx_d + b

令w=(w₁; w₂; ......; w_d)，x = (x₁; x₂; ......; x_d)，使用矩阵乘法写为向量形式：

f(x) = w^Tx + b

在w和b的值确定后（w=(w₁; w₂; ......; w_d)），整个模型就得以确定，其中，权重向量w可以直观表达各个属性的重要性。

2. 单一变量线性回归（Single Variable Linear Regression）

给定数据集 D = {(x₁, y₁), (x₂, y₂), (x₃, y₃), ......, (x_m, y_m)}，其中 x_i = (x_i1, x_i2, x_i3, ......, x_id)，y_i ∈ R，线性回归想要学到一个线性模型，以尽可能准确地预测实值输出标记。

首先考虑最简单的情况：输入的属性数目为1

目标：

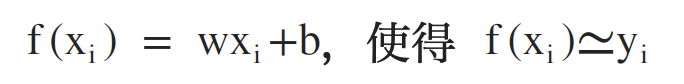
误差函数（均方误差）：

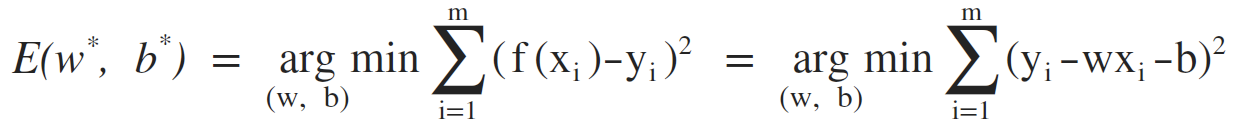
基于均方误差最小化进行模型求解的方法称之为：最小二乘法。

所以，求解w和b的值，使得E(w, b)最小化的过程，称之为线性回归的最小二乘参数估计，将E(w, b) 分别对w和b进行求导：

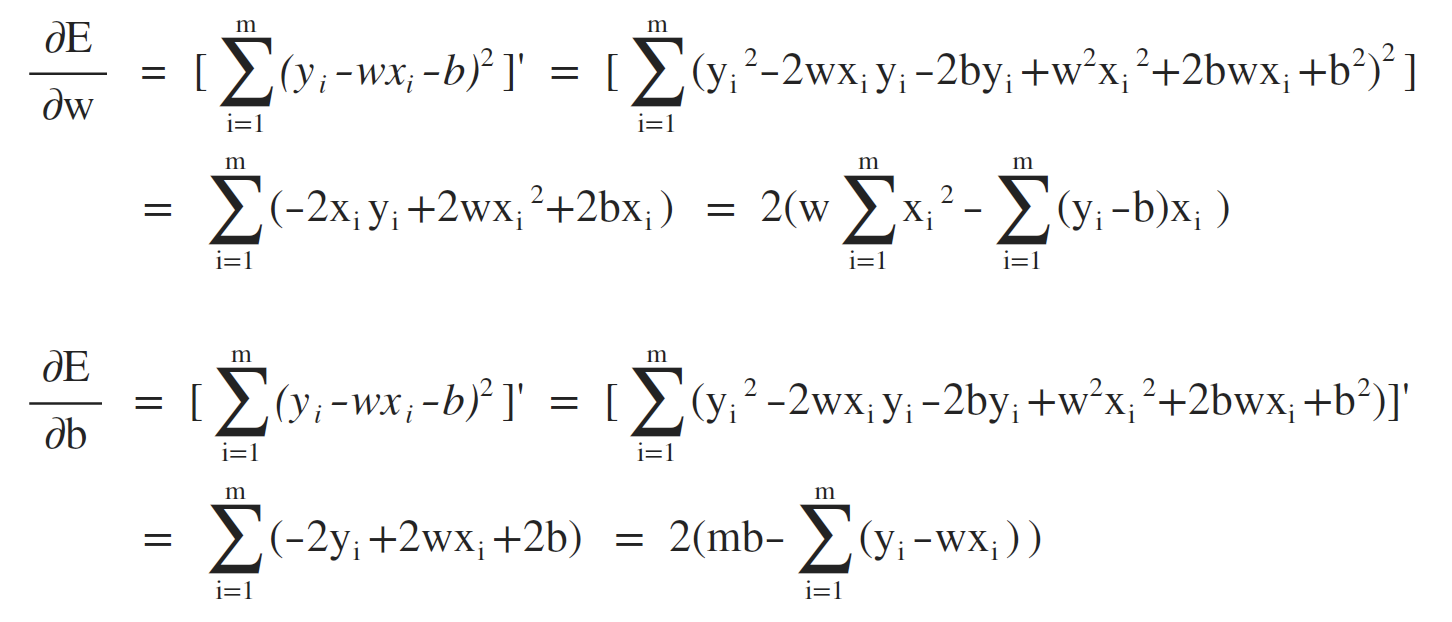
故w和b的最优闭式解为：

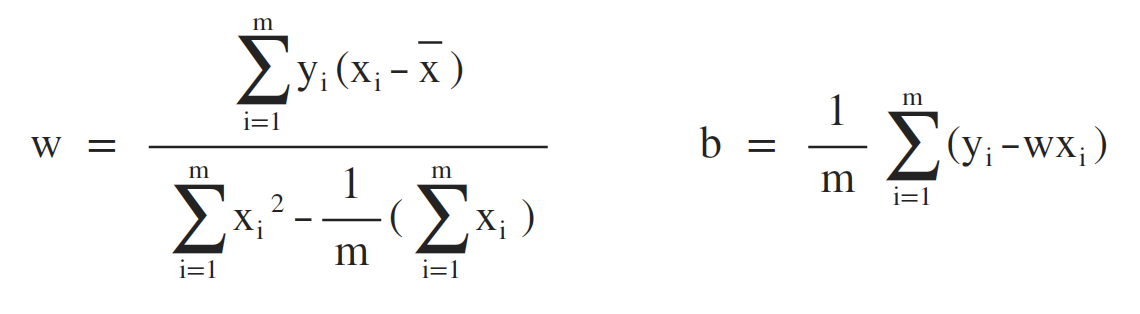
附：对于离散属性，可以对其进行连续化处理，例如，[0, 1] 表示从低到高，则可以使用 [0, 0.5, 1] 来分别表示低、中、高。如果离散属性间属于无序关系，假定有k个属性，则可以转化为K维向量，例如，白人、黑人、黄人对应 (0, 0, 1)、(0, 1, 0)、(1, 0, 0)。

3. 多元线性回归（Multivariate Linear Regression）

从单一变量线性回归推广至更一般的情形：数据集D中的样本由d个属性描述，即：多元变量线性回归。

目标：

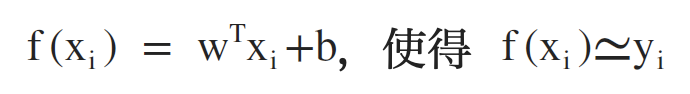
令 w = (w; b)，将数据集D表示为一个 m * (d+1) 的矩阵X，最后一个元素恒置为1，故有：

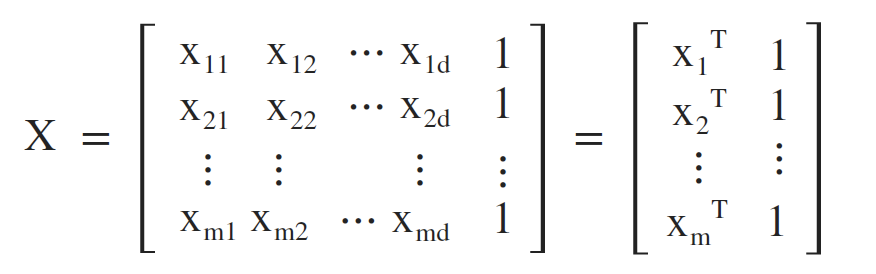
令标记为向量形式 y = (y_1; y_2; ......; y_m)，则有：

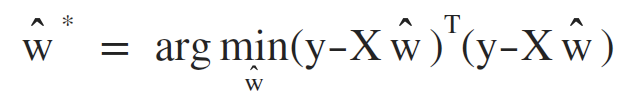
故令：

求导：

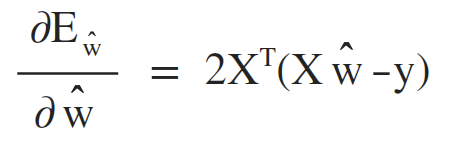
最后求得的多元线性回归模型为：

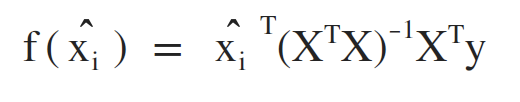
4. 对数几率回归 (Logistic Regression)

阶跃函数 (Unit-step Function)：

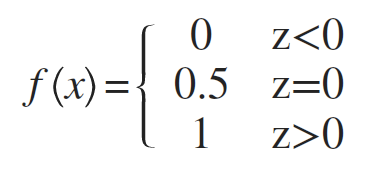
然而阶跃函数不连续，无法作为替代函数使用，所以选择使用Sigmoid函数来代替阶跃函数：

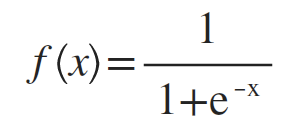
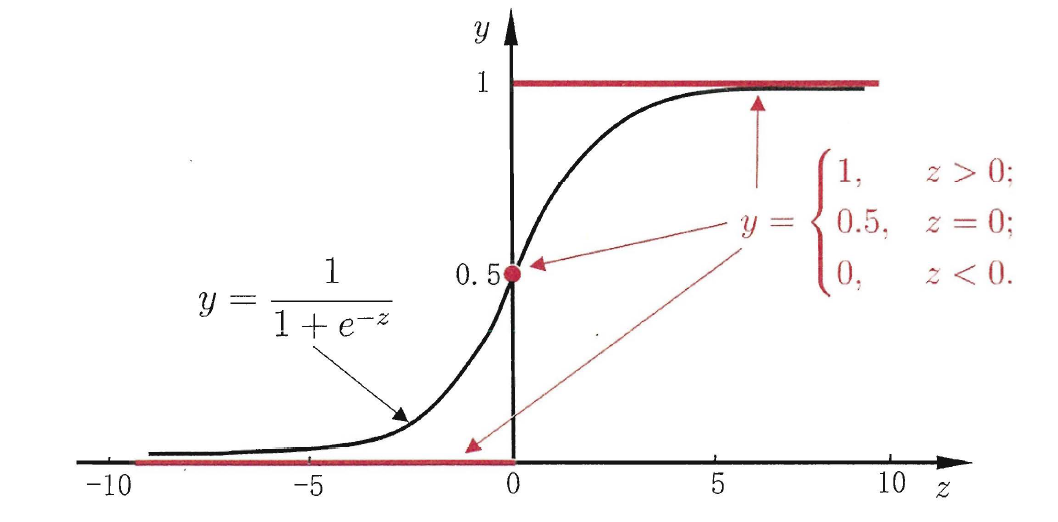
将 f(x)=w^Tx+b 代入Sigmoid函数：

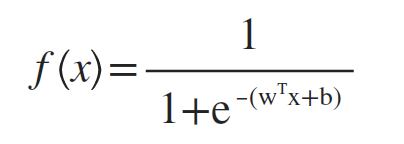
可以推出：

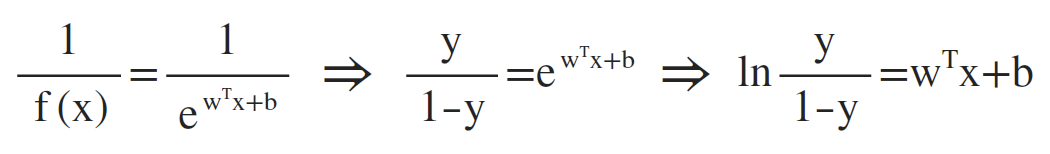
从上面推导的最终结果可以看出，y为输入量x被模型预测为正例的可能性，相应的，1-y则是被预测为反例的可能性，所以 ln(y/1-y) 被称之为对数几率（log odds, logit），所以该模型称为对数几率回归，虽然基于回归，但是实现的功能却是分类，同线性回归一样，当w和b的值确定，模型就得以确定。

特点：

1. 直接对分类结果可能性进行建模，无需事先假设数据分布；
2. 不仅预测类别，还可以得到近似概率预测；
3. logit函数时任意阶可导的凸函数，数学性质优良，很多数值优化算法可以直接用于求取最优解。