Gradient Optimization

Gradient Optimization

Gradient Descent

• Batch Gradient Descent
• Mini-Batch Gradient Descent
• Stochastic Gradient Descent

Mini-Batch Gradient Descent

• 参数
  • Mini-Batch Size: 一个Batch样本所含的样本数
• 参数效果
  • 通过设置Mini-Batch Size可以将Mini-Batch转为Stochastic Gradient Descent和Bath Gradient Descent
  • 当Mini-Batch Size == m时, Mini-Batch Gradient Descent为Batch Gradient Descent; 当Mini-Batch Size == 1时, Mini-Batch Gradient Descent为Stochastic Gradient Descent; 一般Mini-Batch Size的大小为2的幂次方, 主要考虑到与计算机内存对齐, 一般Mini-Batch Size设置在64-512
• 特点对比
  • Batch Gradient Descent: 当数据量大的时候程序运行很慢
  • Stochastic Gradient Descent: 一般不采用此方法, 因为此Gradient Descent方法每迭代一个样本就会更新参数\(W\)和\(b\), 在梯度下降的时候有很多噪音; 但是它可以应用到在线学习上
  • Mini-Batch Gradient Descent: 当数据量较大的时候可以加快收敛速度, 但是当在梯度下降的时候, 容易产生震荡(oscillate), 如图

  

  • 其中, +表示\(J_{min}\), 在使用Mini-Batch Gradient Descent的时候, 容易在数值方向产生震荡, 我们期望的是缩小竖直方向上的震荡, 在水平方向上加快收敛的速率, 对于这个问题, 解决方案是在Update Parameters的时候, 采用Momentum, RMSProp或者Adam的方法更新参数\(W\)和\(b\), 在下面就会提到

处理震荡

• 指数权重均值(Exponentially Weighted Average, 简称EMA), 后面的Momentum, RMSProp和Adam都需要EMA
  • 以一年的中所有天数的温度为例, 如图

  

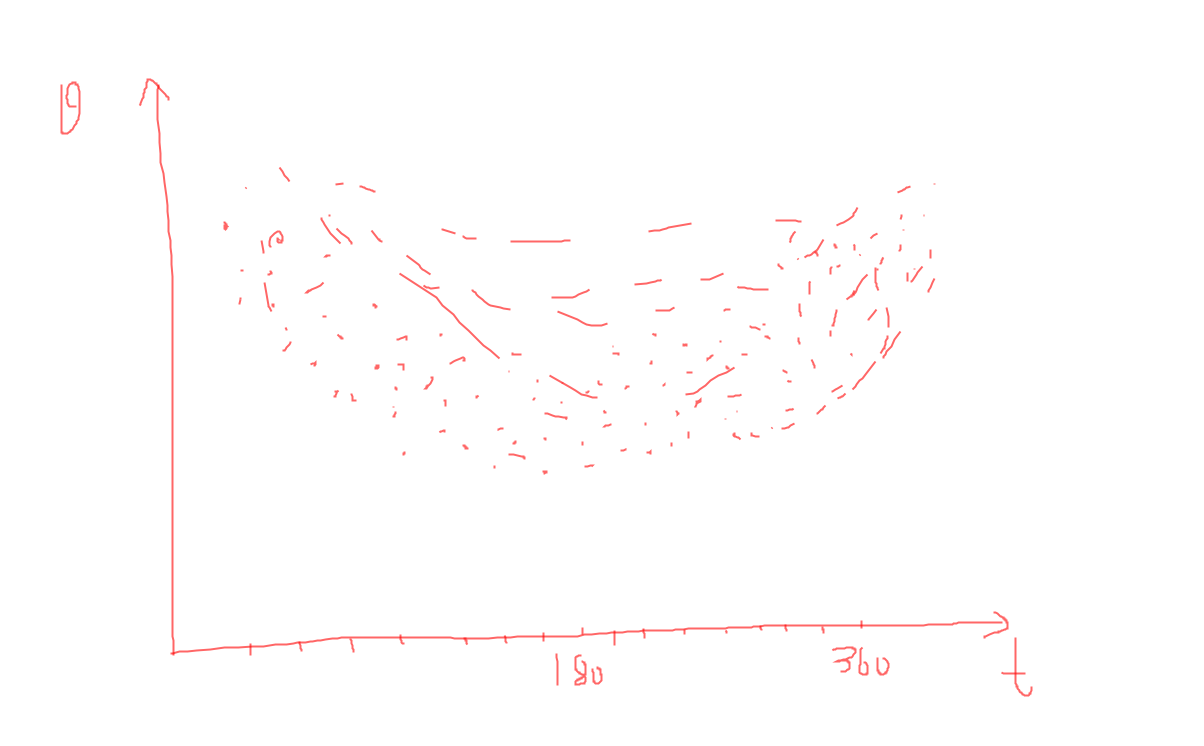
  • 由上图可知, \(\theta\)为气温, \(t\)为天数, 总体来说中间时刻气温低一点, 两侧高一点
  • 定义
    • \(v_t=\beta{v_{t-1}}+(1-\beta)\theta_t\), 其中\(\beta\)为EMA中的一个参数, 一般他的取值范围在\(0.9\le \beta \le 0.99\); \(v_t\)表示的就是EMA; \(\theta_t\)为第\(t\)天的气温; \(\beta{v_t}\)表示的是前\(t\)天的关注度, 后面的\((1-\beta)\theta_t\)是对当前天气温的关注度, 最左侧的\(v_t\)才是我们对当前天的EMA; EMA公式有递归的感觉

• Momentum

  • 公式
    • \(v_{dW^{[l]}}=\beta{v_{dW^{[l]}}}+(1-\beta)dW^{[l]}\), 其中, \(dW^{[l]}\)是第\(l\)层的梯度矩阵, 其他与EMA中的是一样的
    • 返现与EMA中不同的是这里的\(\beta{v_{dW^{[l]}}}\)不是\(\beta{v_{dW^{[l-1]}}}\), 因为我们在实现该算法的时候采用先默认赋予0值, 再在每一次迭代时累加, 下面的RMSProp和Adam也是如此
  • 更新参数
    • \(W^{[l]}=W^{[l]}-\alpha{v_{dW^{[l]}}}\)

• RMSProp

  • 公式
    • \(s_{dW^{[l]}}=\beta{v_{dW^{[l]}}}+(1-\beta)(dW^{[l]})^2\), 其中, 与Momentum不同的就是此处\((dW^{[l]})^2\)
  • 更新参数
    • \(W^{[l]}=W^{[l]}-\alpha{dW^{[l]}\over{\sqrt{s_{dW^{[l]}}+\epsilon}}}\), 其中\(\epsilon \approx 10^{-8}\)

• Adam

  • Adam算法是Momentum与RMSProp的结合
  • 公式
    • \(v_{dW^{[l]}}=\beta_1{v_{dW^{[l]}}}+(1-\beta_1)dW^{[l]}\)
    • \(v^{correct}_{dW^{[l]}}={v_{dW^{[l]}}\over{1-(\beta_1)^t}}\), 其中t表示深度学习算法迭代到第t次, 这一步是\(v_{dW^{[l]}}\)的修正, 在后面即使使用\(v^{correct}_{dW^{[l]}}\)
    • \(s_{dW^{[l]}}=\beta_2{v_dW^{[l]}}+(1-\beta_1)(dW^{[l]})^2\)
    • \(s^{correct}_{dW^{[l]}}={s_{dW^{[l]}}}\over{1-(\beta_2)^t}\),其中t表示深度学习算法迭代到第t次, 这一步是\(s_{dW^{[l]}}\)的修正, 在后面即使使用\(s^{correct}_{dW^{[l]}}\)
  • Adam结合了之前的Momentum与RMSProp算法, 同时增加了校正EMA的步骤, 因为在Momentum和RMSProp算法都有\(\beta\)和\(s\), 所有在这里为了区分, 使用了\(v\)与\(s\), \(\beta_1\)与\(\beta_2\)
  • 更新参数
    • \(W^{[l]}=W^{[l]}-\alpha{v_{dW^{[l]}}^{[l]}\over{\sqrt{s_{dW^{[l]}}+\epsilon}}}\), 其中\(\epsilon \approx 10^{-8}\)

使用代码实现的大致思路

• 选择Mini-Batch Gradient Descent
• Shuffle原始数据
• 选择Mini-Batch Size进行Gradient Descent
• 在迭代Update Parameters时, 先为Momentum, RMSProp或者Adam需要的\(v\), \(s\)变量赋予0值, 维度与对应的\(dW\)一致
• 迭代即可

学习率\(\alpha\)的衰减

• 一般来说我们只需要直接固定\(\alpha\)的值, 随后根据结果进行调整, 但是在数据量很大的时候就会比较浪费时间, 于是使用到了\(alpha\)的衰减
• 定义
  • \(\alpha={1\over{1+decay\_rate\times{epoch}}}\alpha_0\)