堆排序（python实现）

　堆排序是利用最大最或最小堆，废话不多说：

先给出几个概念：

二叉树：二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”

完全二叉树：除最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干结点。

满二叉树： 除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。

堆：堆是一种数据结构，类似树根结构，如图，但是不一定是二叉树。

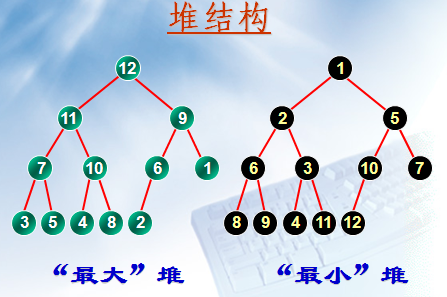
二叉堆：二叉堆是一种特殊的堆，二叉堆是完全二元树（二叉树）或者是近似完全二元树（二叉树），包括最大堆和最小堆。

最大堆：父结点的键值总是大于或等于任何一个子节点的键值，即根节点为最大数字

最小堆：父结点的键值总是大于或等于任何一个子节点的键值，即根节点为最小数字

堆排序步骤：

1.将数据构建成堆，这里的堆指完全二叉树（不一定是满二叉树）

2.将堆调整为最小堆或最大堆

3.此时堆顶已经为最大数或最小数，可以对下面的分支堆再进行调堆即可，此处采用的是将堆顶数取出，再调堆

本人愚钝，网上代码不慎明了，根据自己的思路写了一下，不足之处，请多多指教

1.首先实现将数组按照堆打印

 def PrintArrayTree(arr):
     frontRowSum=1 #Number of digits in front of n-1 rows
     row=1      #row n(start from 1)
     for i in range(0,len(arr)):
         if i==frontRowSum:
             frontRowSum=frontRowSum+2**row #Number of digits in front of n rows
             print("\n")#the next row
             row=row+1
         print (arr[i],end="  ") #print digits
     print("Over")

 arr=[10,9,8,7,6,5,4,3,2,1,234,562,452,23623,565,5,26]
 PrintArrayTree(arr)

运行结果如下：

10

9 8

7 6 5 4

3 2 1 234 562 452 23623 565

5 26
print Over

2.构建完了堆，我想实现在堆内任意查找，找到他的子节点和父节点，代码如下：

 def FindNode(arr,row,cloumn):

     if row<1 or cloumn<1:
         print("the number of row and column must be greater than 1")
         return
     if cloumn>2**(row-1):
         print("this row just ",2**(row-1),"numbers")
         return

     frontRowSum=0
     CurrentRowSum=0
     for index in range(0,row-1):
         CurrentRowSum=2**index  #the number of  digits in current row
         frontRowSum=frontRowSum+CurrentRowSum #the number of  digits of all rows
     NodeIndex=frontRowSum+cloumn-1   #find the location of the node in the array by row and cloumn

     if NodeIndex>len(arr)-1:
         print("out of this array")
         return

     currentNode=arr[NodeIndex]

     childIndex=NodeIndex*2+1

     print("Current Node:",currentNode)

     if row==1:              #row 1 have no parent node
         print("no parent node!")
     else:                   #the parent node ofcurrent node
         parentIndex=int((NodeIndex-1)/2)
         parentNode=arr[parentIndex]
         print("Parent Node:",parentNode)

     if childIndex+1>len(arr):   #print leftChild node
         print("no left child node!")
     else:
         leftChild=arr[childIndex]
         print("Left Child Node:",leftChild)

     if childIndex+1+1>len(arr):     #print rightChild node
         print("no left right node!")
     else:
         rightChild=arr[childIndex+1]
         print("Right Child Node:",rightChild)

     print("\n")

 arr=[10,9,8,7,6,5,4,3,2,1,234,562,452,23623,565,5,26]
 FindNode(arr,1,1)
 FindNode(arr,2,2)
 FindNode(arr,4,1)

代码运行结果如下：

Current Node: 10
no parent node!
Left Child Node: 9
Right Child Node: 8

Current Node: 8
Parent Node: 10
Left Child Node: 5
Right Child Node: 4

Current Node: 3
Parent Node: 7
Left Child Node: 5
Right Child Node: 26

此代码在堆排序中没有直接用到，但是提供了一些思路

3.按照堆排序步骤，建堆之后需要进行堆调整，接下来进行堆调整，先实现单个叉（某个节点及其子孩子）的进行排序，直接借鉴FindNode里面的代码，将当前节点分别与其左右孩子比较就行了，本文意在实现最小堆，即将小的节点作为父节点

def MinSort(arr,row,cloumn):

    if row<1 or cloumn<1:
        print("the number of row and column must be greater than 1")
        return
    if cloumn>2**(row-1):
        print("this row just ",2**(row-1),"numbers")
        return

    frontRowSum=0
    CurrentRowSum=0
    for index in range(0,row-1):
        CurrentRowSum=2**index  #the number of  digits in current row
        frontRowSum=frontRowSum+CurrentRowSum  #the number of  digits of all rows
    NodeIndex=frontRowSum+cloumn-1 #find the location of the node in the array by row and cloumn

    if NodeIndex>len(arr)-1:
        print("out of this array")
        return

    currentNode=arr[NodeIndex]

    childIndex=NodeIndex*2+1

    print("Current Node:",currentNode)

    if row==1:
        print("no parent node!")
    else:
        parentIndex=int((NodeIndex-1)/2)
        parentNode=arr[parentIndex]
        print("Parent Node:",parentNode)

    if childIndex+1>len(arr):
        print("no left child node!")
    else:
        leftChild=arr[childIndex]
        print("Left Child Node:",leftChild)

        if currentNode>leftChild:
            print("swap currentNode and leftChild")
            temp=currentNode
            currentNode=leftChild
            leftChild=temp
            arr[childIndex]=leftChild

    if childIndex+1>=len(arr):
        print("no right child node!")
    else:
        rightChild=arr[childIndex+1]    

        print("Right Chile Node:",rightChild)

        if currentNode>rightChild:
            print("swap rightCild and leftChild")
            temp=rightChild
            rightChild=currentNode
            currentNode=temp
            arr[childIndex+1]=rightChild

    arr[NodeIndex]=currentNode 

arr=[10,9,8,7,6,5,4,3,2,1,234,562,452,23623,565,5,26]
print("initial array:",arr)
MinSort(arr,1,1)
print("result array:",arr)

运行结果如下，可以看出对于第一个节点，其自孩子为9，8，已经实现将节点与最小的自孩子进行交换，保证父节点小于任何一个子孩子

initial array: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 234, 562, 452, 23623, 565, 5, 26]
Current Node: 10
no parent node!
Left Child Node: 9
swap currentNode and leftChild
Right Chile Node: 8
swap rightCild and leftChild
result array: [8, 10, 9, 7, 6, 5, 4, 3, 2, 1, 234, 562, 452, 23623, 565, 5, 26]

4.已经实现对单个节点和子孩子进行比较，保证父节点小于孩子，将堆内所有拥有孩子的节点进行排序，即可调整为最小堆，代码如下：

def MinHeap(arr):

    frontRowSum=1
    row=1
    for i in range(0,len(arr)):
        if i==frontRowSum:
            frontRowSum=frontRowSum+2**row #the number of  digits of all rows
            print("\n") # next row
            row=row+1
        print (arr[i],end="  ")
    print("row",row)

    rowIndex=row-1    #the last row have no child node
    print("rowIndex",rowIndex)

    column=2**(rowIndex-1)  #the number of digits of current row

    print("column",column)

    number=len(arr)

    while rowIndex>0:   #sort the nodes that have child nodes from the last number to the first number
        if number<=2**(rowIndex-1):
            rowIndex=rowIndex-1
            column=2**(rowIndex-1)

        print("sort",rowIndex,column)
        MinSort(arr,rowIndex,column)

        number=number-1

        column=column-1

arr=[10,9,8,7,6,5,4,3,2,1,234,562,452,23623,565,5,26]
print("initial array:",arr)
PrintArrayTree(arr)
MinHeap(arr)
print("result array:",arr)
PrintArrayTree(arr)

运行结果如下，可以看到最小数字已经位于顶端，实现最小堆

initial array: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 234, 562, 452, 23623, 565, 5, 26]

10

9 8

7 6 5 4

3 2 1 234 562 452 23623 565

5 26
print Over

.......
result array: [1, 10, 4, 9, 2, 8, 5, 7, 3, 6, 234, 562, 452, 23623, 565, 5, 26]

1

10 4

9 2 8 5

7 3 6 234 562 452 23623 565

5 26
print Over

4.最小值已经到顶端，将最小值依次取出，然后再调整堆，再取出，就完成堆排序。代码如下：

 def HeapSort(arr):
     arr2=[]
     for i in range(0,len(arr)):
         MinHeap(arr)
         arr2.append(arr[0])
         del arr[0]
     return arr2

 arr=[10,9,8,7,6,5,4,3,2,1,234,562,452,23623,565,5,26]
 print("initial array:",arr)
 PrintArrayTree(arr)
 resultArr=HeapSort(arr)
 print("result array:",resultArr)
 PrintArrayTree(resultArr)

运行结果如下：

initial array: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 234, 562, 452, 23623, 565, 5, 26]
10

9 8

7 6 5 4

3 2 1 234 562 452 23623 565

5 26
print Over

10

9 8

7 6 5 4

3 2 1 234 562 452 23623 565

5 26

.........

result array: [1, 2, 3, 4, 5, 5, 6, 7, 8, 9, 10, 26, 234, 452, 562, 565, 23623]
1

2 3

4 5 5 6

7 8 9 10 26 234 452 562

565 23623
print Over

5.后续工作：

1)代码需要优化

2）感觉堆排序有点类似冒泡排序

3）需要检查代码的健壮性

4）后续需要计算分析代码的复杂度

1)优化之后的程序如下：写法还能再优化，但继续优化会影响可读性

 def MinSort(arr,start,end):
     import math
     arrHeight=0
     for index in range(0,end-start):
         if index==2**(arrHeight+1)-1:
             arrHeight=arrHeight+1

     for NodeIndex in range(2**(arrHeight)-2,-1,-1):
         currentNode=arr[NodeIndex+start]
         childIndex=NodeIndex*2+1+start

         if childIndex+1>len(arr):
             continue
         else:
             leftChild=arr[childIndex]            

             if currentNode>leftChild:
                 temp=currentNode
                 currentNode=leftChild
                 leftChild=temp
                 arr[childIndex]=leftChild
                 arr[NodeIndex+start]=currentNode 

         if childIndex+1>=len(arr):
             continue
         else:
             rightChild=arr[childIndex+1]
             if currentNode>rightChild:

                 temp=rightChild
                 rightChild=currentNode
                 currentNode=temp
                 arr[childIndex+1]=rightChild
                 arr[NodeIndex+start]=currentNode 

 def HeapSort(arr):
     for i in range(0,len(arr)-1):
         MinSort(arr,i,len(arr))

 arr=[10,9,8,7,6,5,4,3,2,1,234,562,452,23623,565,5,26]       

 print("Initial array:\n",arr)
 HeapSort(arr)
 print("Result array:\n",arr)

运行结果：

Initial array:
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 234, 562, 452, 23623, 565, 5, 26]
Result array:
[1, 2, 3, 4, 5, 5, 6, 7, 8, 9, 10, 26, 234, 452, 562, 565, 23623]