3Sum探讨（Java）

探讨一下leetcode上的3Sum：

Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Note: The solution set must not contain duplicate triplets.

For example, given array S = [-1, 0, 1, 2, -1, -4],

A solution set is:
[
  [-1, 0, 1],
  [-1, -1, 2]
]

1.暴力解法
时间复杂度高达O(n^3)

public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> lists =new ArrayList<List<Integer>>();
        for(int i=0;i<nums.length-2;i++) {
            for (int j = i + 1; j < nums.length-1; j++) {
                for(int z=j+1;z<nums.length;z++){
                    if(nums[i]+nums[j]+nums[z]==0){
                        List<Integer> list =new ArrayList<Integer>();
                        list.add(nums[i]);
                        list.add(nums[j]);
                        list.add(nums[z]);
                        lists.add(list);
                    }
                }
            }
        }
        return lists;
    }

运行结果：

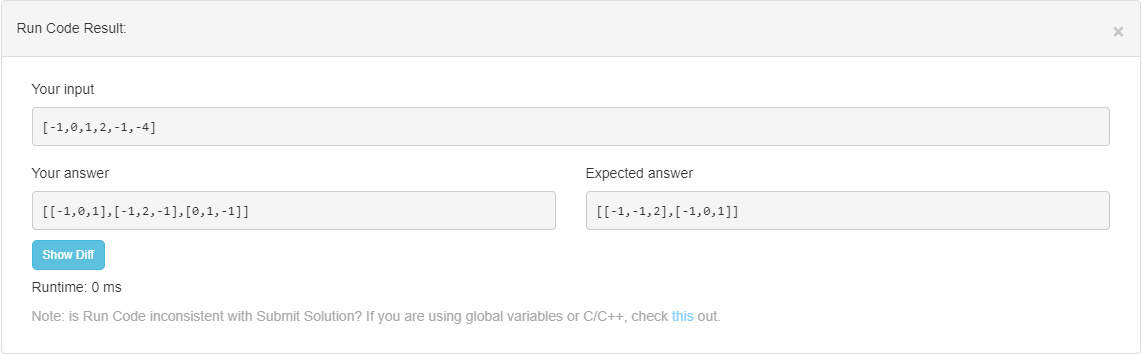
结果不尽人意，有个重复的。我想过如果使用list排重的话。必然先要对list进行排序，然后对比是否相等，如果相等，再剔除掉一样的。代码如下：

    public static List<List<Integer>> three(int[] nums){
        List<List<Integer>> lists =new ArrayList<List<Integer>>();
        for(int i=0;i<nums.length-2;i++) {
            for (int j = i + 1; j < nums.length-1; j++) {
                for(int z=j+1;z<nums.length;z++){
                    if(nums[i]+nums[j]+nums[z]==0){
                        List<Integer> list =new ArrayList<Integer>();
                        boolean flag = true;
                        list.add(nums[i]);
                        list.add(nums[j]);
                        list.add(nums[z]);
                        Collections.sort(list);
                        for(int k=0;i<lists.size();i++){
                            if(list.equals(lists.get(i))){
                                flag = false;
                            }
                        }
                        if(flag){
                        lists.add(list);
                        }
                    }
                }
            }
        }
        return lists;
    }

运行结果：

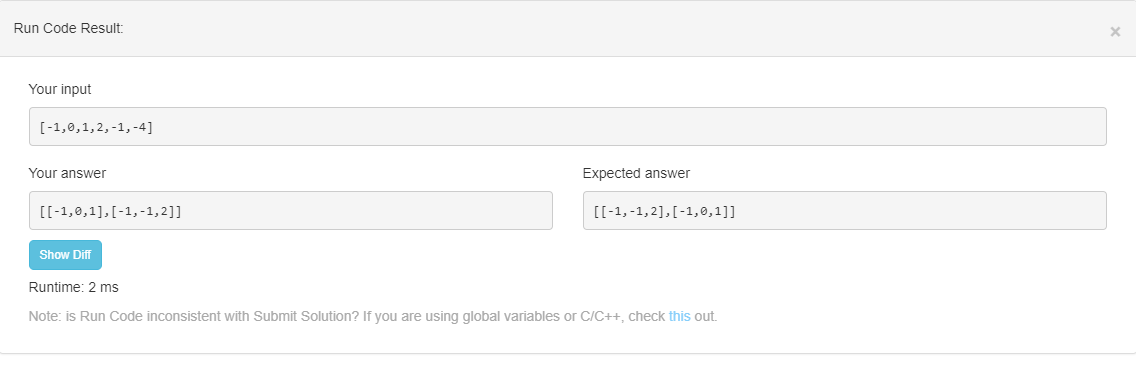
看着貌似问题解决了，但是Runtime=2ms，时间有点长，时间复杂度太高了。

上交的时候爆出来一个错误：

既然结果都能运行出来，为什么还爆数组越界呢？我也看不出来什么毛病。

2.使用map

时间复杂度为O(n+n^2)，即O(n^2)

    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> lists =new ArrayList<List<Integer>>();
        Map<Integer,Integer> map =new HashMap<Integer,Integer>();
        for(int i=0;i<nums.length;i++){
            map.put(num[i],i);
        }
        for(int i=0;i<nums.length;i++){
            for(int j=i+1;j<nums.length;j++) {
                int res=0-nums[i]-nums[j];
                if(map.containsKey(res)&&map.get(res)!=i&&map.get(res)!=j){
                    List<Integer> list =new ArrayList<Integer>();
                    list.add(res);
                    list.add(nums[i]);
                    list.add(nums[j]);
                    lists.add(list);
                }
            }
        }
        return lists;
    }

这个的运行结果让人头疼。

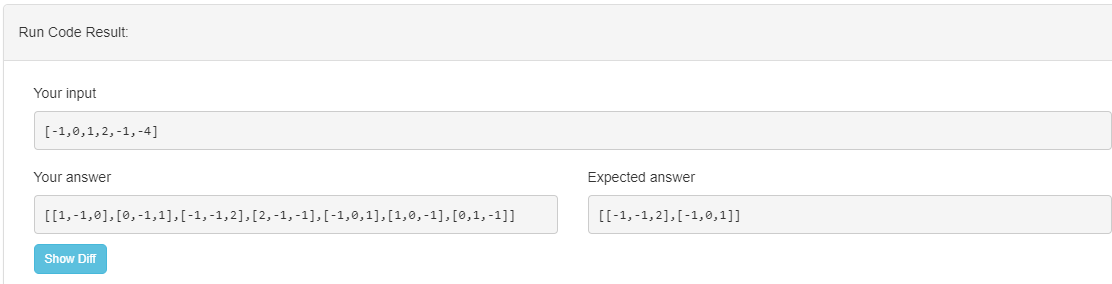
有没有好的办法可以排重，如果这样的话，时间复杂度是O(n^2)：

    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> lists =new ArrayList<List<Integer>>();
        Map<Integer,Integer> map =new HashMap<Integer,Integer>();
        for(int i=0;i<nums.length;i++){
            for(int j=i+1;j<nums.length;j++) {
                int res=0-nums[i]-nums[j];
                if(map.containsKey(res)){
                    List<Integer> list =new ArrayList<Integer>();
                    list.add(res);
                    list.add(nums[i]);
                    list.add(nums[j]);
                    lists.add(list);
                }
            }
            map.put(nums[i],i);
        }
        return lists;
    }

运行结果：

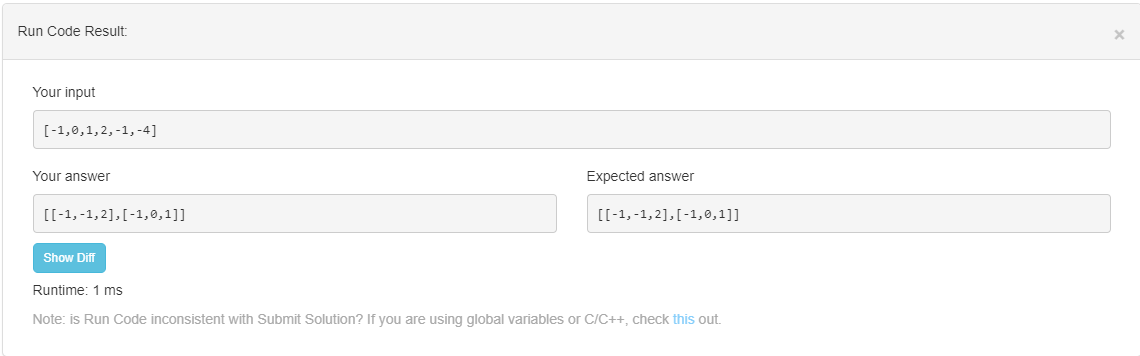
这下结果正确了，提交一下：

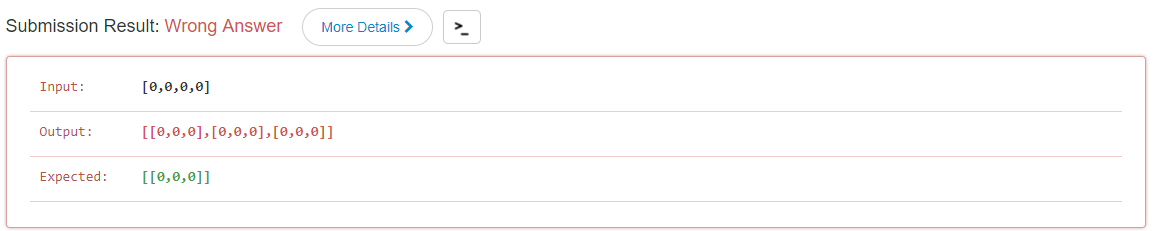
对于上面的数组，算法是不成立的。我把上面的list排重写进里面，但是就是解决不了问题。请高手帮我解决问题，共同学习。

附上leetcode这个问题的地址：

15. 3Sum