拓扑排序&关键路径

拓扑排序：AOV网

概念

example：选课问题:AOV网

顶点活动（Activity On Vertex）网是指用顶点表示活动，而用边集表示活动关系的有向图。
在这个例子中，课程为结点，而有向边表示着课程的依赖关系。

算法

1.定义一个队列Q，并把所有入度为0的结点加入队列。

2.取队首结点，输出（存储）。然后删去所有从它出发的边（非必要），并令这些边达到的顶点的入度减1，如果某个顶点的入度减为0，则将其加入队列。

3.反复进行步骤2，直到队列为空。如果此时入队次数恰好为N，说明排序成功，G为有向无环图；否则，拓扑排序失败，G有环。
(PS:如果要求有多个度为0的节点时，输出编号最小的点，可以使用优先队列）

关键路径：AOE网

边活动（Activity On Edge）网是指带权的边集表示活动，而用顶点表示事件的有向图，其中边权表示完成活动所需要的时间。

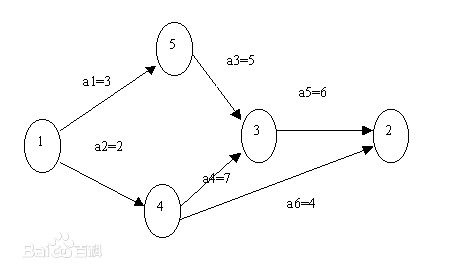
在上图中，每个顶点代表先前的事件已完成，可以进行下一个事件。

一般来说，AOE网用来表示一个工程的进行过程，AOE网中同样不能有环。
对于一个工程来说，多个子进程可以同时进行。

AOE网中入度为0的点名为源点（上图1），出度为0的点名为汇点上图2）。从所有源点出发，到达所有汇点所需的时间即为完成工程的总时间，也即为到达所有顶点所需的时间。

求解这个时间，即是要求解AOE网的最长路径，也叫作关键路径，关键路径上的活动就叫作关键活动。

拓扑排序就是其中一种可以解决该问题的算法。只需对AOV的算法稍加修改即可：
增加一个最早到达各顶点时间的数组。
在步骤2中，遍历一个顶点u指向的所有下一个顶点v时：
若：
\[
time[u]+weight_{uv}>time[v]
\]
则：
\[
time[v]：=time[u]+weight_{uv}
\]