LeetCode 62.不同路径（C++）

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

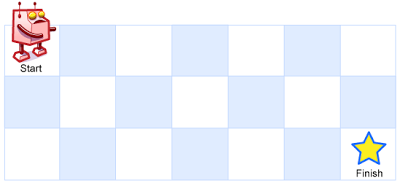
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

可以观察规律，矩阵中数字表示起点到这个地方有多少条路。

1	1	1	1	1
1	2	3	4	5
1	3	6	10	15

发现坐标(i,j)路的条数，可以通过关系式：way[i][j] = way[i - 1][j] + way[i][j - 1];计算

#include <iostream>
#include <vector>
#include <algorithm>
#include <memory>
#include <numeric>

using namespace std;

static int x = []() {std::ios::sync_with_stdio(false); cin.tie(); return ; }();

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int> > way(m, vector<int>(n, ));

        for (int i = ; i < m; ++i) {
            for (int j = ; j < n; ++j) {
                way[i][j] = way[i - ][j] + way[i][j - ];
            }
        }

        return way[m - ][n - ];
    }
};

int main()
{
    Solution A;
    int m = , n = ;

    cout << A.uniquePaths(m, n);

    system("PAUSE");
    return ;
}

注意：memset()是按字节赋值，只能够赋值-1或0。

当我们赋值1时，1转换为二进制00000001，占1字节，int型为4字节，因此实际上赋值的是：0000 0001,0000 0001,0000 0001,0000 0001

也就是16843009

int ptr** = new int*[m];
for(int i = ; i < m; ++i)
{
    ptr[m] = new int[n];
}

....

for(int i = ; i < m;++i)
    delete[] ptr[m];
}
delete []ptr;