【CodeForces - 1034B】Little C Loves 3 II

@中文题意@

n*m的矩阵，当两个点(x1, y1)与(x2, y2)曼哈顿距离为3时可以将两个点匹配。每个点只能够与一个点匹配。求最多能可以匹配多少个点。
n,m <= 10^9

(xi,yi) and (xj,yj) is defined as |xi−xj|+|yi−yj|.

@分析@

【这种题也只能够手算小数据来找规律……】
首先弄清楚一个上界：对于任意的n∗mn∗m n*mn∗m矩阵，如果n与m都为奇数，则答案最大为nm-1；否则答案最大为nm。
不妨假设n <= m。
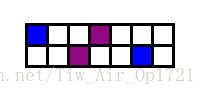
当 n = 1 的时候，我们只能横着进行匹配。我们手算几组数据，可以用如下图的方法可以把1∗61∗6 1*61∗6所有点都匹配。

再手算几组，我们发现这样一个规律：对于任意一个1∗m1∗m 1*m1∗m，如果m%6<=3，则能匹配的点数为m-m%6；否则能匹配的点数为m-6+m%6。
【具体的证明应该可以用归纳法证明，请容许我偷一下懒qwq】

当 n = 2 的时候。2∗22∗2 2*22∗2显然无解，2∗32∗3 2*32∗3的矩阵中间那一列的元素没有任何元素能跟它们匹配，所以最大匹配点数也只能为4。2∗42∗4 2*42∗4，2∗52∗5 2*52∗5可以采用下列所示的方法全部匹配完。

2∗62∗6 2*62∗6矩阵可以把它拆成两个1∗61∗6 1*61∗6的矩阵，每个矩阵内部可以全部匹配完。
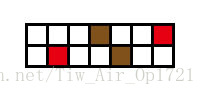
然后！学长们就是被2∗72∗7 2*72∗7的矩阵卡掉了。实际上2∗72∗7 2*72∗7不能构造出全部匹配的情况的。如图：两个蓝色块只能与两个紫色块匹配，所以紫色块只能与蓝色块匹配。同理，两个红色块只能与两个棕色块匹配，所以棕色块只能与红色块匹配。然后有一个块既要和蓝色块匹配又要和棕色块匹配，所以不可能~

所以2∗72∗7 2*72∗7最多只能配对12个点。
然后，最关键的来了。对于一个2∗m2∗m 2*m2∗m（m>=7），如果m为偶数，我们可以把m拆成若干个4与6的和，即将原矩阵拆成若干个2∗42∗4 2*42∗4矩阵与2∗62∗6 2*62∗6矩阵。对于这些矩阵我们可以把所有点匹配完，所以我们自然也就可以匹配完2∗m2∗m 2*m2∗m的所有点；反之，如果m为奇数，我们可以先将2∗m2∗m 2*m2∗m分成2∗52∗5 2*52∗5与2∗(m−5)2∗(m−5) 2*(m-5)2∗(m−5)两个部分，2∗52∗5 2*52∗5可以匹配完。又因m-5是个偶数，所以奇数也可以得到相似的结论。
即：2∗m（m>=7）2∗m（m>=7） 2*m（m&gt;= 7）2∗m（m>=7）的矩阵，答案总可以达到上界2∗m2∗m 2*m2∗m

下一步，当n = 3的时候。
3∗33∗3 3*33∗3，3∗43∗4 3*43∗4，3∗53∗5 3*53∗5的构造如下：

3∗63∗6 3*63∗6就可以分成3个1∗61∗6 1*61∗6拼出，就不画图了。
于是，对于一个3∗m3∗m 3*m3∗m的矩阵，一样地，如果m是偶数，就将m拆成若干个4与6的和；否则就拆成(m-3)与3。所以，3∗m（m>=3）3∗m（m>=3） 3*m（m&gt;=3）3∗m（m>=3）的答案也总是可以达到上界

对于n = 4，我们已知4∗24∗2 4*24∗2，4∗34∗3 4*34∗3可以构造出来。4∗44∗4 4*44∗4可以拆成两个4∗24∗2 4*24∗2。类似的推理，4∗m（m>=4）4∗m（m>=4） 4*m（m&gt;=4）4∗m（m>=4）的答案总可以达到上界。

对于n = 5，我们已知5∗25∗2 5*25∗2，5∗35∗3 5*35∗3，5∗45∗4 5*45∗4可以构造出来。因此5∗m（m>=5）5∗m（m>=5） 5*m（m&gt;=5）5∗m（m>=5）的答案总可以达到上界。

对于n = 6，我们已知6∗16∗1 6*16∗1可以构造出来。因此6∗m（m>=6）6∗m（m>=6） 6*m（m&gt;=6）6∗m（m>=6）的答案总可以达到上界。

然后，对于n>6。如果n为偶数，可以把n拆成若干个4与6的和；否则如果m为偶数，可以把n拆成若干个4与6的和；否则，可以把n拆成(n-3)与3，然后重复上面的推理。因此n∗m（n>6,m>n）n∗m（n>6,m>n） n*m（n&gt;6, m&gt;n）n∗m（n>6,m>n）的答案总可以达到上界。

至此，本题就Over了。

@代码@

#include<cstdio>
#include<algorithm>
using namespace std;
int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    if( n > m ) swap(n, m);
    if( n ==  ) {
        if( m %  ==  )
            printf("%d\n", m);
        else if( m %  <=  )
            printf("%d\n", m-(m%));
        else printf("%d\n", m-(-m%));
    }
    else if( n ==  && m ==  )
        printf("%d\n", );
    else if( n ==  && m ==  )
        printf("%d\n", );
    else if( n ==  && m ==  )
        printf("%d\n", );
    else {
        if( n %  ==  && m %  ==  )
            printf("%I64d\n", 1LL*n*m-);
        else printf("%I64d\n", 1LL*n*m);
    }
}

另外解法：

这道题…

可以说是打表吧

首先我们可以观察到，对于任意一个1∗61∗6 1*61∗6或者2∗42∗4 2*42∗4的格子，都是可以填满的，

那也就说如果有一边长能被6或者4给整除，那就是可以填满的

然后对于5*5以下的了，我们可以直接打表预处理出来（因为有一些特殊情况吧）

#include<bits/stdc++.h>

using namespace std ;
int D[][]={ {,,,,},
               {,,,,},
               {,,,,},
               {,,,,},
               {,,,,}};
int main( )
{
    int n,m;
    scanf("%d%d",&n,&m);
    if(n<m)
    swap(n,m);
    long long ans=;
    if(m==)
    {
        ans+=n/*;
        n=n%;
        ans+=D[][n-];
    }
    else if(n%== || m%==)
    ans=(long long )n*m;
    else if(n%== || m%==)
    ans=(long long )n*m;
    else if(n==&&m==)
    ans=;
    else if(n<=&&m<=)
    ans=D[n-][m-];
    else
        ans=(long long )n*m/*;
    printf("%I64d\n",ans);
    return ;
}