NOIP 模拟赛

思路：求 n , m 的 gcd，然后用 n , m 分别除以 gcd；若 n 或 m 为偶数，则输出 1/2.

　　特别的，当 n = m = 1 时，应输出 1/1

  1. #include <algorithm>
  2. #include <iostream>
  3. #include <cstring>
  4. #include <cstdio>
  5. using namespace std;
  6. typedef long long LL;
  7. LL n, m;
  8.  
  9. LL gcd(LL x, LL y) {
  10.     return y ==  ? x : gcd(y, x % y);
  11. }
  12.  
  13. int main() {
  14.     freopen("line.in","r",stdin);
  15.     freopen("line.out","w",stdout);
  16.     cin >> n >> m;
  17.     if (n == m && m == ) return printf("1/1\n"), ;
  18.     LL tmp = gcd(n, m);
  19.     n /= tmp; m /= tmp;
  20.     if (!(n & ) || !(m & )) return printf("1/2\n"), ;
  21.  
  22.     fclose(stdin); fclose(stdout);
  23.     return ;
  24. }

考场代码

正解：题目要求的是比值，故当 m 与 n 不互质时，我们可以求出 m 和 n 的最大公约数 d，并将 m /= d, n /= d，并不影响结果。故我们现在假定 m 和 n 互质。若m 和 n 中有一个为偶数， 那么根据对称性， 答案就是 1/2。 如果 m 和 n 均为奇数，那么答案就是(n*m+1) / (2*m*n）。

  1. #include<iostream>
  2. #include<cstring>
  3. #include<cstdlib>
  4. #include<cstdio>
  5. #include<cmath>
  6. using namespace std;
  7. typedef long long LL;
  8. LL n, m, d;
  9.  
  10. LL gcd(LL x, LL y) {
  11.     return x % y ? gcd(y, x % y) : y;
  12. }
  13.  
  14. int main() {
  15.     freopen("line.in","r",stdin);
  16.     freopen("line.out","w",stdout);
  17.     cin >> n >> m;
  18.     d = gcd(n, m);
  19.     n /= d, m /= d;
  20.     if ((n + m) & ) cout << "1/2" << endl;
  21.     else cout << (n * m + ) /  << "/" << n * m << endl;
  22.     return ;
  23. }

正解

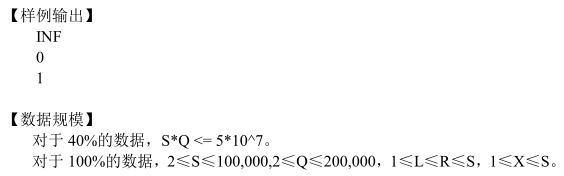
思路：线段树维护是否有浓雾。一开始都没有，建树时每个位置的值都赋为 1；若进行 1 或 2 操作，用 flag 标记，因为是区间直接赋值，所以两种操作只需要一个标记即可。查询写错了，导致100 -> 10，对题意理解稍有偏差。

  1. #include <algorithm>
  2. #include <cstring>
  3. #include <cstdio>
  4. using namespace std;
  5. const int N = ;
  6. int n, m, k, x, y;
  7. struct nond {
  8.     int ll, rr;
  9.     int sum;
  10.     int flag;
  11. } tree[N << ];
  12.  
  13. inline void update(int now) {
  14.     tree[now].sum = tree[now << ].sum + tree[now <<  | ].sum;
  15. }
  16.  
  17. inline void down(int now) {
  18.     if (tree[now].flag == ) {
  19.         tree[now << ].flag = ;
  20.         tree[now <<  | ].flag = ;
  21.         tree[now << ].sum = tree[now << ].rr - tree[now << ].ll + ;
  22.         tree[now <<  | ].sum = tree[now <<  | ].rr - tree[now <<  | ].ll + ;
  23.     }
  24.     else {
  25.         tree[now << ].flag = -;
  26.         tree[now <<  | ].flag = -;
  27.         tree[now << ].sum = ;
  28.         tree[now <<  | ].sum = ;
  29.     }
  30.     tree[now].flag = ;
  31.     return ;
  32. }
  33.  
  34. inline void build(int now, int l, int r) {
  35.     tree[now].ll = l; tree[now].rr = r;
  36.     tree[now].flag = ; tree[now].sum = ;
  37.     if (l == r) return ;
  38.     int mid = (l + r) >> ;
  39.     build(now << , l, mid);
  40.     build(now <<  | , mid + , r);
  41.     update(now);
  42. }
  43.  
  44. inline void change(int now, int l, int r) {
  45.     if (tree[now].ll == l && tree[now].rr == r) {
  46.         tree[now].flag = -;
  47.         tree[now].sum = ;
  48.         return ;
  49.     }
  50.     if (tree[now].flag != ) down(now);
  51.     int mid = (tree[now].ll + tree[now].rr) >> ;
  52.     if (l <= mid && mid < r) change(now << , l, mid), change(now <<  | , mid + , r);
  53.     else if (r <= mid) change(now << , l, r);
  54.     else change(now <<  | , l, r);
  55.     update(now);
  56. }
  57.  
  58. inline void become(int now, int l, int r) {
  59.     if (tree[now].ll == l && tree[now].rr == r) {
  60.         tree[now].flag = ;
  61.         tree[now].sum = tree[now].rr - tree[now].ll + ;
  62.         return ;
  63.     }
  64.     if (tree[now].flag != ) down(now);
  65.     int mid = (tree[now].ll + tree[now].rr) >> ;
  66.     if (l <= mid && mid < r) become(now << , l, mid), become(now <<  | , mid + , r);
  67.     else if (r <= mid) become(now << , l, r);
  68.     else become(now <<  | , l, r);
  69.     update(now);
  70. }
  71.  
  72. inline int query(int now, int l, int r) {
  73.     if (tree[now].ll == l && tree[now].rr == r)
  74.         return tree[now].sum;
  75.     if (tree[now].flag != ) down(now);
  76.     int mid = (tree[now].ll + tree[now].rr) >> ;
  77.     if (l <= mid && mid < r) return query(now << , l, mid) + query(now <<  | , mid + , r);
  78.     else if (r <= mid) return query(now << , l, r);
  79.     else return query(now <<  | , l, r);
  80. }
  81.  
  82. int main() {
  83.     freopen("explore.in","r",stdin);
  84.     freopen("explore.out","w",stdout);
  85.     scanf("%d%d", &n, &m);
  86.     build(, , n);
  87.     for (int i = ; i <= m; ++i) {
  88.         scanf("%d%d", &k, &x);
  89.         if (k == ) { scanf("%d", &y); change(, x, y); }
  90.         else if (k == ) { scanf("%d", &y); become(, x, y); }
  91.         else {
  92.             if (query(, x, x) == ) printf("0\n");
  93.             else {
  94.                 if (query(, , x) == x || query(, x, n) == n - x + )
  95.                     printf("INF\n");
  96.                 else for (int j = ; j <= (n >> ); ++j) {
  97.                     int tmp = query(, x - j, x + j);
  98.                     if (tmp != j <<  | ) { printf("%d\n", tmp); break; }
  99.                 }
  100.             }
  101.         }
  102.     }
  103.     fclose(stdin); fclose(stdout);
  104.     return ;
  105. }

考场代码

  1. #include<iostream>
  2. #include<algorithm>
  3. #include<cstdio>
  4. #include<cstdlib>
  5. #define fortodo(i, f, t) for (i = f; i <= t; i++)
  6. using namespace std;
  7.  
  8. int lsd[], rsd[], lsid[], rsid[], cov[], segsize;
  9. bool emp[];
  10.  
  11. int SEG_Build(int L, int R) {
  12.     int Nid = ++segsize;
  13.     lsd[Nid] = L;
  14.     rsd[Nid] = R;
  15.     emp[Nid] = true;
  16.     cov[Nid] = ;
  17.     if (L == R) lsid[Nid] = rsid[Nid] = -;
  18.     else {
  19.         lsid[Nid] = SEG_Build(L, (L + R) / );
  20.         rsid[Nid] = SEG_Build((L + R) /  + , R);
  21.     };
  22.     return Nid;
  23. };
  24.  
  25. bool SEG_Empty(int Nid) {
  26.     if (cov[Nid] == ) return true;
  27.     if (cov[Nid] == ) return false;
  28.     return emp[Nid];
  29. };
  30.  
  31. void SEG_Reemp(int Nid) {
  32.     emp[Nid] = SEG_Empty(lsid[Nid]) && SEG_Empty(rsid[Nid]);
  33. };
  34.  
  35. void SEG_Inherit(int Nid) {
  36.     if (cov[Nid] == -) return;
  37.     if (lsd[Nid] == rsd[Nid]) return;
  38.     cov[lsid[Nid]] = cov[Nid];
  39.     cov[rsid[Nid]] = cov[Nid];
  40.     cov[Nid] = -;
  41.     SEG_Reemp(Nid);
  42. };
  43.  
  44. void SEG_Paint(int Nid, int L, int R, int Color) {
  45.     SEG_Inherit(Nid);
  46.     if ((L == lsd[Nid]) && (R == rsd[Nid])) {
  47.         cov[Nid] = Color;
  48.         return;
  49.     };
  50.     int Div = (lsd[Nid] + rsd[Nid]) / ;
  51.     if (L >  Div) SEG_Paint(rsid[Nid], L, R, Color);
  52.     if (R <= Div) SEG_Paint(lsid[Nid], L, R, Color);
  53.     if ((L <= Div) && (R > Div)) {
  54.         SEG_Paint(lsid[Nid], L, Div, Color);
  55.         SEG_Paint(rsid[Nid], Div + , R, Color);
  56.     };
  57.     SEG_Reemp(Nid);
  58. };
  59.  
  60. bool SEG_Query(int Nid, int L, int R) {
  61.     SEG_Inherit(Nid);
  62.     if (SEG_Empty(Nid)) return true;
  63.     if ((L == lsd[Nid]) && (R == rsd[Nid])) return SEG_Empty(Nid);
  64.     int Div = (lsd[Nid] + rsd[Nid]) / ;
  65.     if (L >  Div) return SEG_Query(rsid[Nid], L, R);
  66.     if (R <= Div) return SEG_Query(lsid[Nid], L, R);
  67.     return SEG_Query(lsid[Nid], L, Div) && SEG_Query(rsid[Nid], Div + , R);
  68. };
  69.  
  70. int S, Q;
  71. int i, j;
  72. int Opt, X, Y;
  73.  
  74. void Answer(int P) {
  75.     if (!SEG_Query(, P, P)) {
  76.         printf("0\n");
  77.         return;
  78.     };
  79.     if ((SEG_Query(, , P)) || (SEG_Query(, P, S))) {
  80.         printf("INF\n");
  81.         return;
  82.     };
  83.     int L, R, M, Ans[];
  84.     L = ; R = P;
  85.     while (L < R) {
  86.         M = (L + R) / ;
  87.         if (SEG_Query(, M, P)) R = M;
  88.         else L = M + ;
  89.     };
  90.     Ans[] = L;
  91.     L = P; R = S - ;
  92.     while (L < R) {
  93.         M = (L + R + ) / ;
  94.         if (SEG_Query(, P, M))
  95.             L = M;
  96.         else
  97.             R = M - ;
  98.     };
  99.     Ans[] = L;
  100.     printf("%d\n", Ans[] - Ans[] + );
  101. };
  102.  
  103. int main() {
  104.     freopen("explore.in", "r", stdin);
  105.     freopen("explore.out", "w", stdout);
  106.     scanf("%d%d", &S, &Q);
  107.     segsize = ;
  108.     SEG_Build(, S);
  109.     fortodo(i, , Q) {
  110.         scanf("%d%d", &Opt, &X);
  111.         if (Opt != ) scanf("%d", &Y);
  112.         if (Opt == ) SEG_Paint(, X, Y, );
  113.         if (Opt == ) SEG_Paint(, X, Y, );
  114.         if (Opt == ) Answer(X);
  115.     };
  116.     return ;
  117. };

正解

思路：

　　1.暴搜  写挂了，样例都过不了

　　2.树形DP  不会写 后来讲题时发现自己想法是错的

　　3.并查集  将直接连接两个有苹果的节点的边打上标记，记录边权和，但仍会存在多个苹果间接相连的情况，没有想到解决办法

然后我就交了唯一一个过了样例但是最不靠谱的 3

然后就暴零了 T^T。。。

  1. #include <algorithm>
  2. #include <iostream>
  3. #include <cstring>
  4. #include <cstdio>
  5. using namespace std;
  6. const int M = ;
  7. int n, m, tot;
  8. int t[M], fc[M];
  9. int fa[M], f[M];
  10. struct nond {
  11.     int u, v, w;
  12.     int flag;
  13. }e[M];
  14.  
  15. int find(int x) {
  16.     return fa[x] == x ? x : fa[x] = find(fa[x]);
  17. }
  18.  
  19. bool flag = false;
  20. inline void dfs(int now) {  //可以明显看到没写完 因为不会写了 qwq
  21.     if (f[now] == ) flag = ;
  22.  
  23. }
  24.  
  25. long long ans;
  26. int main() {
  27.     freopen("apple.in","r",stdin);
  28.     freopen("apple.out","w",stdout);
  29.     scanf("%d%d", &n, &m);
  30.     for (int i = ; i < n; ++i) fa[i] = i;
  31.     for (int i = ; i < n; ++i) {
  32.         scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
  33.         e[i].flag = ;
  34.     }
  35.     for (int i = ; i <= m; ++i) {
  36.         scanf("%d", &t[i]);
  37.         f[t[i]] = ;
  38.     }
  39.     for (int i = ; i < n; ++i) {
  40.         if (f[e[i].u] ==  && f[e[i].v] == ) {
  41.             e[i].flag = ;
  42.             ans += e[i].w;
  43.             ++tot;
  44.             continue;
  45.         }
  46.         int x = find(e[i].u), y = find(e[i].v);
  47.         fa[x] = y;
  48.  
  49.     }
  50.     if (tot == m - ) cout << ans;
  51.     else {
  52.         for (int i = ; i < n; ++i)
  53.             ++fc[find(i)];
  54.         for (int i = ; i < n; ++i) {
  55.             if (fc[i] > ) dfs(i);
  56.             if (tot == m - ) break;
  57.         }
  58.         cout << ans;
  59.     }
  60.     fclose(stdin); fclose(stdout);
  61.     return ;
  62. }

考场代码

正解：

　　

  1. #include <algorithm>
  2. #include <iostream>
  3. #include <cstdlib>
  4. #include <cstring>
  5. #include <string>
  6. #include <cstdio>
  7. #include <cmath>
  8. #define REP(i, n) for (int i = 0; i < (n); ++i)
  9. #define FOR(i, a, b) for (int i = (a); i <= (b); ++i)
  10. #define ROF(i, a, b) for (int i = (a); i >= (b); --i)
  11. #define FEC(p, u) for (edge *p = G.head[u]; p; p = p->nxt)
  12. using namespace std;
  13. typedef long long LL;
  14. LL inf = 1LL<<;
  15.  
  16. int n, rt;
  17. bool a[];
  18. LL f[], g[];
  19.  
  20. struct edge {
  21.     int b, len;
  22.     edge *nxt;
  23. } e[], *le;
  24. struct graph {
  25.     edge *head[];
  26.     void init() {
  27.         le = e;
  28.         REP(i, n) head[i] = NULL;
  29.     }
  30.     void add(int x, int y, int z) {
  31.         le->b = y, le->len = z, le->nxt = head[x], head[x] = le++;
  32.     }
  33. } G;
  34.  
  35. int fa[];
  36. LL pre[];
  37. int q[];
  38. void init() {
  39.     int k, u, v, w;
  40.     scanf("%d%d", &n, &k);
  41.     G.init();
  42.     REP(i, n-) {
  43.         scanf("%d%d%d", &u, &v, &w);
  44.         G.add(u, v, w);
  45.         G.add(v, u, w);
  46.     }
  47.     while (k--) {
  48.         scanf("%d", &u);
  49.         a[u] = true;
  50.     }
  51.     rt = u;
  52. }
  53.  
  54. void bfs() {
  55.     int R = ;
  56.     q[] = rt;
  57.     REP(L, n)
  58.     FEC(p, q[L]) if (p->b != fa[q[L]]) {
  59.         fa[p->b] = q[L];
  60.         pre[p->b] = p->len;
  61.         q[++R] = p->b;
  62.     }
  63. }
  64.  
  65. void work() {
  66.     ROF(i, n - , ) {
  67.         int x = q[i];
  68.         if (a[x]) {
  69.             FEC(p, x) if (p->b != fa[x]) g[x] += f[p->b];
  70.             f[x] = g[x]+pre[x];
  71.         }
  72.         else {
  73.             FEC(p, x) if (p->b != fa[x])    f[x] += f[p->b];
  74.             g[x] = inf;
  75.             FEC(p, x) if (p->b != fa[x]) g[x] = min(g[x], f[x] - f[p->b] + g[p->b]);
  76.             f[x] = min(f[x], g[x]+pre[x]);
  77.         }
  78.     }
  79. }
  80.  
  81. int main() {
  82.     freopen("apple.in", "r", stdin);
  83.     freopen("apple.out", "w", stdout);
  84.     init();
  85.     bfs();
  86.     work();
  87.     cout << f[rt] << endl;
  88.     return ;
  89. }

正解

NOIP 模拟赛的更多相关文章

  1. NOIP模拟赛20161022

    NOIP模拟赛2016-10-22 题目名 东风谷早苗 西行寺幽幽子 琪露诺 上白泽慧音 源文件 robot.cpp/c/pas spring.cpp/c/pas iceroad.cpp/c/pas ...

  2. contesthunter暑假NOIP模拟赛第一场题解

    contesthunter暑假NOIP模拟赛#1题解: 第一题:杯具大派送 水题.枚举A,B的公约数即可. #include <algorithm> #include <cmath& ...

  3. NOIP模拟赛 by hzwer

    2015年10月04日NOIP模拟赛 by hzwer    (这是小奇=> 小奇挖矿2(mining) [题目背景] 小奇飞船的钻头开启了无限耐久+精准采集模式!这次它要将原矿运到泛光之源的矿 ...

  4. 大家AK杯 灰天飞雁NOIP模拟赛题解/数据/标程

    数据 http://files.cnblogs.com/htfy/data.zip 简要题解 桌球碰撞 纯模拟,注意一开始就在袋口和v=0的情况.v和坐标可以是小数.为保险起见最好用extended/ ...

  5. 队爷的讲学计划 CH Round #59 - OrzCC杯NOIP模拟赛day1

    题目:http://ch.ezoj.tk/contest/CH%20Round%20%2359%20-%20OrzCC杯NOIP模拟赛day1/队爷的讲学计划 题解:刚开始理解题意理解了好半天,然后发 ...

  6. 队爷的Au Plan CH Round #59 - OrzCC杯NOIP模拟赛day1

    题目:http://ch.ezoj.tk/contest/CH%20Round%20%2359%20-%20OrzCC杯NOIP模拟赛day1/队爷的Au%20Plan 题解:看了题之后觉得肯定是DP ...

  7. 队爷的新书 CH Round #59 - OrzCC杯NOIP模拟赛day1

    题目:http://ch.ezoj.tk/contest/CH%20Round%20%2359%20-%20OrzCC杯NOIP模拟赛day1/队爷的新书 题解:看到这题就想到了 poetize 的封 ...

  8. CH Round #58 - OrzCC杯noip模拟赛day2

    A:颜色问题 题目:http://ch.ezoj.tk/contest/CH%20Round%20%2358%20-%20OrzCC杯noip模拟赛day2/颜色问题 题解:算一下每个仆人到它的目的地 ...

  9. CH Round #52 - Thinking Bear #1 (NOIP模拟赛)

    A.拆地毯 题目:http://www.contesthunter.org/contest/CH%20Round%20%2352%20-%20Thinking%20Bear%20%231%20(NOI ...

  10. CH Round #49 - Streaming #4 (NOIP模拟赛Day2)

    A.二叉树的的根 题目:http://www.contesthunter.org/contest/CH%20Round%20%2349%20-%20Streaming%20%234%20(NOIP 模 ...

随机推荐

  1. 改动Android设备信息，如改动手机型号为iPhone7黄金土豪版！

    首先你的手机必需要有ROOT权限,误操作有风险需慎重 请先开启手机的USB调试,防止手机改动后无法启动时导致的无法修复 1.假设你是在手机上改动,直接使用RE文件管理器,编辑/system/build ...

  2. 【POJ 1845】 Sumdiv (整数唯分+约数和公式+二分等比数列前n项和+同余)

    [POJ 1845] Sumdiv 用的东西挺全 最主要通过这个题学了约数和公式跟二分求等比数列前n项和 另一种小优化的整数拆分  整数的唯一分解定理: 随意正整数都有且仅仅有一种方式写出其素因子的乘 ...

  3. 【android】解决Viewpager设置高度为wrap_content无效的方法

    今天发现设置viewpager高度为wrap_content时并没作用.stackoverflow给出了解决方式,就是自己定义viewpager,重写onMesure()方法: public clas ...

  4. emmet教程

    https://www.zfanw.com/blog/zencoding-vim-tutorial-chinese.html https://www.zfanw.com/blog/zencoding- ...

  5. nyoj--1184--为了肾六（动态规划+滚动数组）

    为了肾六 时间限制:4000 ms  |  内存限制:210535 KB 难度:2 描述 最近肾六很流行,goshawk看身边的朋友都用上了apple.自己还用着W年前的Samsung.于是决定去IT ...

  6. Strings are immutable

    It is tempting to use the [] operator on the left side of an assignment, with the intention of chang ...

  7. java9新特性-4-模块化系统: Jigsaw与Modularity

    1.官方Feature 200: The Modular JDK 201: Modular Source Code 220: Modular Run-Time Images 260: Encapsul ...

  8. 基于opencv的手写数字字符识别

    摘要 本程序主要参照论文,<基于OpenCV的脱机手写字符识别技术>实现了,对于手写阿拉伯数字的识别工作.识别工作分为三大步骤:预处理,特征提取,分类识别.预处理过程主要找到图像的ROI部 ...

  9. childNodes.length和form.length的不同

    我们知道,DOM里面提供了element.childNodes.length属性,childNodes 属性返回节点的子节点集合,以 NodeList 对象. 那么childNodes包含哪些节点呢? ...

  10. 因子问题 I - Ugly Numbers

    题目: Ugly numbers are numbers whose only prime factors are 2, 3 or 5 . The sequence 1, 2, 3, 4, 5, 6, ...