alg--分治法

分治--分而治之， 把大的问题分成n个小的问题，分别处理，然后汇总小问题的结果。

具体介绍可以参考这位大哥的blog:
　　https://www.cnblogs.com/steven_oyj/archive/2010/05/22/1741370.html

思考的地方，分治是思想还是算法，递归是思想还是什么？？

-- 个人理解分治是算法的思想，递归是一种实现的思想吧

example：

53. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

一般解法：

int maxSubArray(int* nums, int numsSize) {
    int                 i                   = ;
    int                 j                   = ;
    int                 iSum                = ;
    int                 iMax                = nums[];    

    for (; i < numsSize; iSum = , i++)
    {
        for (j = i; j< numsSize; j++)
        {
            iSum += nums[j];
            if (iMax < iSum) iMax = iSum;
        }
    }
    return iMax;
}

分治解法：

#define MAX_INT(a, b)  ((a > b) ? a : b)
int GetMidMax(int* nums, int iS, int iE)
{
    int                 iMid                = ;
    int                 iMax                = ;
    int                 iSum                = ;
    int                 i                   = ;

    iMid = (iS + iE) / ;
    iSum = iMax = nums[iMid] + nums[iMid + ];

    /* for pre */
    for (i = iMid - ; i >= ; i--)
    {
        iSum += nums[i];
        if (iSum > iMax) iMax = iSum;
    }

    /* for after */
    for (i = iMid + ; i <= iE; i++)
    {
        iSum += nums[i];
        if (iSum > iMax) iMax = iSum;
    }

    return iMax;
}

int GetMaxSubRe(int* nums, int iS, int iE)
{
    int                 iMaxLeft            = ;
    int                 iMaxRight           = ;
    int                 iMaxMid             = ;
    int                 iMid                = ;

    if (iS == iE)
    {
        return ((nums[iS] > ) ? nums[iS] : );
    }

    iMid = (iS + iE) / ; /* mid pos */

    iMaxLeft = GetMaxSubRe (nums, iS, iMid);
    iMaxRight = GetMaxSubRe (nums, iMid + , iE);
    iMaxMid = GetMidMax(nums, iS, iE);

    return MAX_INT(MAX_INT(iMaxRight, iMaxLeft), iMaxMid);

}

int maxSubArray(int* nums, int numsSize) {
    int                 iRet                = ;
    iRet = GetMaxSubRe(nums, , numsSize - );

    return iRet;
}

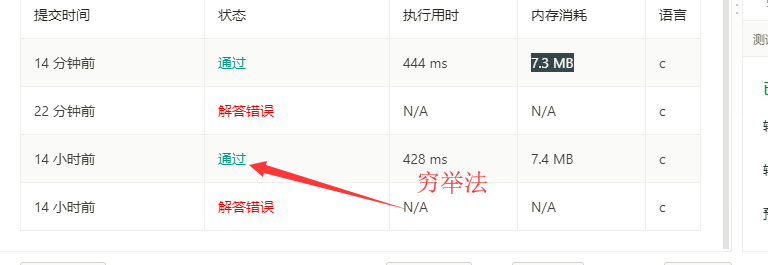
总结：
　　看了运行结果统计，效率没什么提升，和个人理解的不一样，应该是test case的原因。分治的时间效率应该比穷举法好，o(nlogn) < o(n^2)