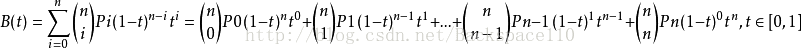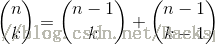n阶贝塞尔曲线绘制(C/C#)

原文:n阶贝塞尔曲线绘制(C/C#)

贝塞尔是很经典的东西，轮子应该有很多的。求n阶贝塞尔曲线用到了 德卡斯特里奥算法（De
Casteljau’s Algorithm）

需要拷贝代码请直接使用本文最后的例程，文章前面的大部分代码都不是最佳实践，是在编程过程中的摸索(走过的弯路)，不过这些示范对笔者今后写算法启发很大。

要完成的功能是根据起点，终点和控制点，绘制n阶贝塞尔曲线

首先看n阶贝塞尔曲线的公式

公式中用了组合数，大数组合数计算也有算法：

简言之就是把  大数乘以大数除以大数  这个过程 转为单纯的累加。

下面来说明一下这个组合数计算的优化过程：

100000 / 100 =  1000

500 + 500 = 1000

上面两个式子计算结果是相等的，但是如果编程实现，

第一个式子就必须使用至少一个Uint32 来存放100000;

但是第二个式子只需要Uint16类型就可以完成整个计算。

通过变换计算方式，可以通过计算机有限的数据大小计算尽可能大的结果。 

贝塞尔曲线也是一种插值算法， 根据起点和终点，通过中间的控制点，插值计算出整条路径

现代的x86，硬件计算浮点都是先转换为double的，所以用double会比float会更快，当然这里只针对英特尔家族复杂指令集产品。

为什么用float不用double是因为PointF是C#自带的结构体{float X;float Y;}，要改为double也是很简单的，全局替换一下数据类型即可

C#数组自带Length属性，但是为了方便移植到C，这里还是使用数组+数组长度作为入参，这样可以很容易的改写为C下面的数组指针+数组长度。

直接实现数学公式是比较简单的，直接贴代码：

public static class Bezier
{
    /// <summary>
    /// 绘制n阶贝塞尔曲线路径
    /// </summary>
    /// <param name="points">输入点</param>
    /// <param name="count">点数(n+1)</param>
    /// <param name="step">步长,步长越小，轨迹点越密集</param>
    /// <returns></returns>
    public static PointF[] draw_bezier_curves(PointF[] points, int count, float step)
    {
        List<PointF> bezier_curves_points = new List<PointF>();
        float t = 0F;
        do
        {
            PointF temp_point = bezier_interpolation_func(t, points, count);    // 计算插值点
            t += step;
            bezier_curves_points.Add(temp_point);
        }
        while (t <= 1 && count > 1);    // 一个点的情况直接跳出.
        return bezier_curves_points.ToArray();  // 曲线轨迹上的所有坐标点
    }
    /// <summary>
    /// n阶贝塞尔曲线插值计算函数
    /// 根据起点，n个控制点，终点 计算贝塞尔曲线插值
    /// </summary>
    /// <param name="t">当前插值位置0~1 ，0为起点，1为终点</param>
    /// <param name="points">起点，n-1个控制点，终点</param>
    /// <param name="count">n+1个点</param>
    /// <returns></returns>
    private static PointF bezier_interpolation_func(float t, PointF[] points, int count)
    {
        PointF PointF = new PointF();
        float[] part = new float[count];
        float sum_x = 0, sum_y = 0;
        for (int i = 0; i < count; i++)
        {
            ulong tmp;
            int n_order = count - 1;    // 阶数
            tmp = calc_combination_number(n_order, i);
            sum_x += (float)(tmp * points[i].X * Math.Pow((1 - t), n_order - i) * Math.Pow(t, i));
            sum_y += (float)(tmp * points[i].Y * Math.Pow((1 - t), n_order - i) * Math.Pow(t, i));
        }
        PointF.X = sum_x;
        PointF.Y = sum_y;
        return PointF;
    }
    /// <summary>
    /// 计算组合数公式
    /// </summary>
    /// <param name="n"></param>
    /// <param name="k"></param>
    /// <returns></returns>
    private static ulong calc_combination_number(int n, int k)
    {
        ulong[] result = new ulong[n + 1];
        for (int i = 1; i <= n; i++)
        {
            result[i] = 1;
            for (int j = i - 1; j >= 1; j--)
                result[j] += result[j - 1];
            result[0] = 1;
        }
        return result[k];
    }
}

使用方法:

// 第一个是起点，最后一个是终点，中间的都是控制点，贝赛尔曲线阶数 = 总点数-1
PointF[] pointList = new PointF[] { new PointF(1.3F, 2.4F), new PointF(2, 3), new PointF(12.3F, 13.2F) };

PointF[] aa = Bezier.draw_bezier_curves(pointList, pointList.Length, 0.001F); // 在起点和终点之间画1/0.001=1000个点
foreach (var item in aa)
{
    // 绘制曲线点
    // 下面是C#绘制到Panel画板控件上的代码
    // panel1.CreateGraphics().DrawEllipse(new Pen(Color.Green), new RectangleF(item, new SizeF(2, 2)));
}

可以很容易的改写成C/C++版，

PointF只是个结构体，{float X；float Y}；

C/C++中数组部分不需要new

Math.Pow()对应于C语言math.h头文件里的 pow()

List<PointF>在C++中可以通过vector实现

在C中可以换成malloc分配个数组，大小推荐使用 (1/step) + 1。

目前为止，只是从数学公式上实现了程序，这个程序有什么问题呢？

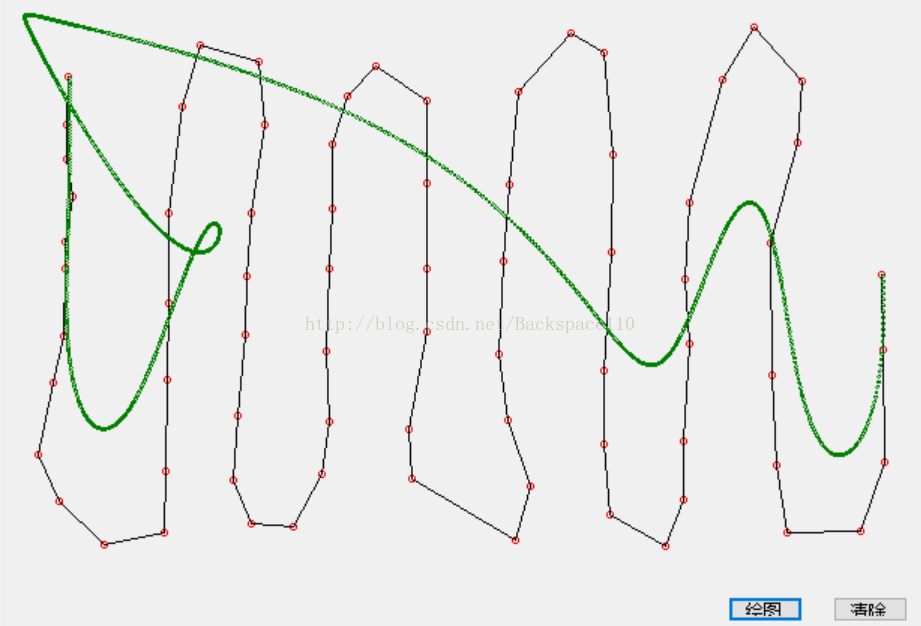
下面放两张图，分别是通过上面的代码计算出来的 4阶和 某n(n很大)阶的巴赛尔曲线，

可以看到阶数过多的时候计算出错了，原因就在于计算组合数函数那里，当阶数过多的时候，组合数中阶乘的计算结果溢出了。

其实仔细观察会发现阶乘计算结果在bezier_interpolation_func函数中又乘以 了一个小数，

这里就是可以改进的地方，阶乘的计算结果既然只是中间值，那么就可以通过某些算法来除掉这个中间值或者通过转化为累加的方式来解决，

就像文章开篇把组合数的 计算公式 n!/(k!*(n-k)!) 简化为 (n-1)!/(k!*(n-k-1)!) + (n-1)!/((k-1)!*(n-k+1)!)  的递归加法一样，bezier_interpolation_func函数也可以通过递归的方式来优化。

使它能够计算更高的阶数而不会溢出(如果有足够的内存空间..)。

下面来看一个改进版的程序

    public static PointF bezier_interpolation_func(float t, PointF[] points, int count)
    {
        if (points.Length < 1)  // 一个点都没有
            throw new ArgumentOutOfRangeException();

        if (count == 1)
            return points[0];
        else
        {
            PointF[] tmp_points = new PointF[count];
            for (int i = 1; i < count; i++)
            {
                tmp_points[i - 1].X = (float)(points[i - 1].X * t + points[i].X * (1 - t));
                tmp_points[i - 1].Y = (float)(points[i - 1].Y * t + points[i].Y * (1 - t));
            }
            return bezier_interpolation_func(t, tmp_points, count - 1);
        }
    }

可以看到将bezier_interpolation_func修改为递归的形式，同时去掉了求组合数的过程。

看一下结果

可以，实现了功能。

然后将递归改为循环，循环的方式有更好的兼容性和效率，特别是某些低端的嵌入式编译器不支持递归方式。

/// 参考: http://blog.csdn.net/Fioman/article/details/2578895
public static PointF bezier_interpolation_func(float t, PointF[] points, int count)
{
    if (points.Length < 1)  // 一个点都没有
        throw new ArgumentOutOfRangeException();

    PointF[] tmp_points = new PointF[count];
    for (int i = 1; i < count; ++i)
    {
        for (int j = 0; j < count - i; ++j)
        {
            if (i == 1) // 计算+搬运数据,在计算的时候不要污染源数据
            {
                tmp_points[j].X = (float)(points[j].X * (1 - t) + points[j + 1].X * t);
                tmp_points[j].Y = (float)(points[j].Y * (1 - t) + points[j + 1].Y * t);
                continue;
            }
            tmp_points[j].X = (float)(tmp_points[j].X * (1 - t) + tmp_points[j + 1].X * t);
            tmp_points[j].Y = (float)(tmp_points[j].Y * (1 - t) + tmp_points[j + 1].Y * t);
        }
    }
    return tmp_points[0];
}

下面是c语言的一个完整程序，不过是打印曲线点的坐标，不太直观。

 #include "stdio.h"
#include "math.h"
#include "assert.h"

typedef struct
{
	float X;
	float Y;
} PointF;

PointF bezier_interpolation_func(float t, PointF* points, int count)
{
	assert(count>0);

	PointF tmp_points[count];
	for (int i = 1; i < count; ++i)
	{
		for (int j = 0; j < count - i; ++j)
		{
			if (i == 1)
			{
				tmp_points[j].X = (float)(points[j].X * (1 - t) + points[j + 1].X * t);
				tmp_points[j].Y = (float)(points[j].Y * (1 - t) + points[j + 1].Y * t);
				continue;
			}
			tmp_points[j].X = (float)(tmp_points[j].X * (1 - t) + tmp_points[j + 1].X * t);
			tmp_points[j].Y = (float)(tmp_points[j].Y * (1 - t) + tmp_points[j + 1].Y * t);
		}
	}
	return tmp_points[0];
}

void draw_bezier_curves(PointF* points, int count, PointF* out_points,int out_count)
{
	float step = 1.0 / out_count;
	float t =0;
	for(int i=0; i<out_count; i++)
	{
		PointF temp_point = bezier_interpolation_func(t, points, count);    // 计算插值点
		t += step;
		out_points[i] = temp_point;
	}
}

int main(int argc, char **argv)
{
	PointF in[3] = {{100,100},{200,200},{300,100}}; // 输入点

	int num = 1000;     // 输出点数
	PointF out[num];    // 输出点数组

	draw_bezier_curves(in,3,out,num);// 二阶贝塞尔曲线

	for(int j=0; j<num; j++)    // 输出路径点
	{
		printf("%d\t X=%f \t Y=%f \r\n",j,out[j].X,out[j].Y);
	}
	return 0;
}

参考连接http://blog.csdn.net/Fioman/article/details/2578895

简介引用连接http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html