k近邻法(k-nearest neighbor, k-NN)

一种基本分类与回归方法

工作原理是：1、训练样本集+对应标签

　　　　　　2、输入没有标签的新数据，将新的数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本最相似数据(最近邻)的分类标签。

　　　　　　3、一般来说，我们只选择样本数据集中前k个最相似的数据。

　　　　　　4、选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

k-近邻算法没有进行数据的训练，直接使用未知的数据与已知的数据进行比较，得到结果。因此，可以说k-邻近算法不具有显式的学习过程。

距离度量：欧氏距离

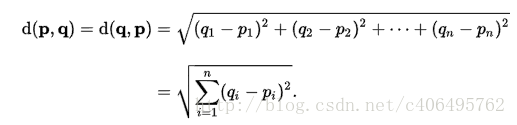
工作流程：

1. 收集数据：可以使用爬虫进行数据的收集，也可以使用第三方提供的免费或收费的数据。一般来讲，数据放在txt文本文件中，按照一定的格式进行存储，便于解析及处理。
2. 准备数据：使用Python解析、预处理数据。
3. 分析数据：可以使用很多方法对数据进行分析，例如使用Matplotlib将数据可视化。
4. 测试算法：计算错误率。
5. 使用算法：错误率在可接受范围内，就可以运行k-近邻算法进行分类。

KNN算法原理代码：

 import numpy as np
 import operator

 def classify0(inx,dataset,labels,k):  #定义一个分类函数，测试数据，数据集，标签集，k个
     datasetsize = dataset.shape[0]  #获取数据集的第一维个数，为了计算测试数据与数据集中每个数据的距离
     diffmat = np.tile(inx,(datasetsize,1)) - dataset #将测试数据在行上重复多次，列上重复一次，也就是不重复，
                                                      # 这样可以与每个数据计算距离
     sqdiffmat = diffmat**2 #距离的平方
     sqdistance = sqdiffmat.sum(axis=1) # 行里的所有元素都加起来，1是行，0是列
     distance = sqdistance**0.5  #距离的平方再开方
     sorteddisindeces = distance.argsort() #距离进行从小到大的排序，返回的是排序后的索引值
     classcount = {} #这个是用来记录取得前k个值后，进行排序的字典， 键：距离对应的标签，值：标签出现的次数
     for i in range(k):
         voteilabel = labels[sorteddisindeces[i]] #键 = 标签（前k个索引值）  键=前k个标签
         classcount[voteilabel] = classcount.get(voteilabel,0) + 1 #        #计算前k个便签出现的次数，次数就是值
     sortedclasscount = sorted(classcount.items(),key=operator.itemgetter(1),reverse=True) #key=operator.itemgetter(1)定义函数，获取对象1值
                                                                                           #按照值进行倒序排，元素格式是
                        #{ [标签，次数],[标签，次数].......}
     return sortedclasscount[0][0] #排完值后，将排行老一的也就是最近距离的标签

 def createDataSet():
     #四组二维特征
     group = np.array([[1,101],[5,89],[108,5],[115,8]])
     #四组特征的标签
     labels = ['爱情片','爱情片','动作片','动作片']
     return group, labels

 if __name__ == '__main__':
     #创建数据集
     group, labels = createDataSet()
     #测试集
     test = [101,20]
     #kNN分类
     test_class = classify0(test, group, labels, 3)
     #打印分类结果
     print(test_class)

使用sklearn运用KNN(鸢尾花数据集)

 from sklearn import datasets
 #导入内置的数据集
 from sklearn.neighbors import KNeighborsClassifier
 #导入sklearn.neighbors 里的KNN算法模块
 import numpy as np

 np.random.seed(0)
 #设置随机种子，这样每次调用随机模块时产生的随机数就是一样的了

 iris=datasets.load_iris()
 #导入鸢尾花数据集（data数据,target标签）

 iris_x=iris.data
 #获取样本数据    type:nadarry
 #是150*4二维数据，代表150个样本，
 # 一共三类花 Iris-Setosa 山鸢尾，Iris-Versicolour 变色鸢尾，Iris-Virginica 维吉尼亚鸢尾
 # 每类有50个样本，每个样本4个属性分别为花萼和花瓣的长、宽

 iris_y = iris.target
 #获取样本标签，是150*1的一维数组, type:nadarry

 indices = np.random.permutation(len(iris_x))
 #permutation接收一个数作为参数(150),产生一个0-149一维数组，只不过是随机打乱的，当然她也可以接收一个一维数组作为参数，结果是直接对这个数组打乱
 #函数shuffle与permutation都是对原来的数组进行重新洗牌（即随机打乱原来的元素顺序）；区别在于shuffle直接在原来的数组上进行操作，改变原来数组的顺序，无返回值。而permutation不直接在原来的数组上进行操作，而是返回一个新的打乱顺序的数组，并不改变原来的数组。
 #b=np.random.permutation(10) 返回的b是nadarry类型

 iris_x_train = iris_x[indices[:-10]]
 iris_y_train = iris_y[indices[:-10]]
 #选取140个数据和标签作为训练数据集和训练数据集的标签

 iris_x_test = iris_x[indices[-10:]]
 iris_y_test = iris_y[indices[-10:]]
 #最后十个作为测试数据集

 knn = KNeighborsClassifier()
 #定义了一个分类器对象
 knn.fit(iris_x_train,iris_y_train)
 #调用knn的训练方法，主要接受两个参数：训练数据集和其样本标签

 iris_y_predict = knn.predict(iris_x_test)
 #调用该对象的测试方法，主要接受一个参数：测试数据集

 probility = knn.predict_proba(iris_x_test)
 #计算各测试样本基于概率的预测

 #score = knn.score(iris_x_test,iris_y_test,sample_weight=None)
 #调用该对象的打分方法，计算出准确率

 print('iris_y_predict=')
 print(iris_y_predict)
 #测试结果

 print('iris_y_test=')
 print(iris_y_test)
 #真实的测试集的标签

 #print('accuracy:')
 #print(score)
 #正确率

 #print(neighborpoint)
 #临点
 print(probility)
 #概率预测

第一步：定义分类器对象

knn = KNeighborClassifier()

第二步：训练样本

knn.fit(x_train,y_train)

第三步：测试数据集

y_predict = knn.predict(x_test)

第四步：显示预测概率，显示测试数据集标签，显示预测数据集标签

probility = knn.predict_proba(x_test)

y_test

y_predict

方法解读：

np.tile（A,B）

 >>> import numpy
 >>> numpy.tile([0,0],5) #在列方向上重复[0,0]5次，默认行1次
 array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

 >>> numpy.tile([0,0],(1,3)) #行方向上重复1次，列方向上重复3次
 array([[0, 0, 0, 0, 0, 0]])

sum()函数

 #0：压缩为一行，每列的元素全都加起来
       第一维的元素，相应位置加起来
 >>> np.sum([[0, 1], [0, 5]], axis=0)
 array([0, 6])

 #1：压缩为一列，每一行的元素都加起来
       第二维的元素加起来
 >>> np.sum([[0, 1], [0, 5]], axis=1)
 array([1, 5])

argsort函数

argsort函数是Numpy模块中的函数，返回的是数组值从小到大的索引值。

#One dimensional array:一维数组
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)           #也可以 x.argsort()
array([1, 2, 0])

#Two-dimensional array:二维数组
>>> x = np.array([[0, 3], [2, 2]])
>>> x
array([[0, 3],
[2, 2]])

>>> np.argsort(x, axis=0) #按列排序
array([[0, 1],
[1, 0]])

>>> np.argsort(x, axis=1) #按行排序
array([[0, 1],
[0, 1]])

>>> x = np.array([3, 1, 2])
>>> np.argsort(x) #按升序排列
array([1, 2, 0])
>>> np.argsort(-x) #按降序排列
array([0, 2, 1])

字典的get()方法

dict.get(key, default=None)

>>>dict = {'A':1, 'B':2}
>>>print(dict.get('A'))
1
>>>print(dict.get('C'))
None
>>>print(dict.get('A', 0))  #A存在字典中时，返回对应值，不在时返回0
>>>1
>>>print(dict.get('C', 0))
>>>0

operator.itemgetter函数

operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为一些序号。要注意，operator.itemgetter函数获取的不是值，而是定义了一个函数，通过该函数作用到对象上才能获取值。

 a = [1,2,3]
 >>> b=operator.itemgetter(1)     //定义函数b，获取对象的第1个域的值
 >>> b(a)
 2
 >>> b=operator.itemgetter(1,0)   //定义函数b，获取对象的第1个域和第0个的值
 >>> b(a)
 (2, 1) 

sorted函数

Python内置的排序函数sorted可以对list或者iterator进行排序。

sorted(iterable[, cmp[, key[, reverse]]])

（1）iterable指定要排序的list或者iterable

（2）cmp为函数，指定排序时进行比较的函数，可以指定一个函数或者lambda函数，如：

      students = [('john', 'A', 15), ('jane', 'B', 12), ('dave', 'B', 10)]

      sorted(students, key=lambda student : student[2])

（3）key为函数，指定取待排序元素的哪一项进行排序，函数用上面的例子来说明，代码如下：

       sorted(students, key=lambda student : student[2]) 

       例如要通过student的第三个域排序，可以这么写：

　　sorted(students, key=operator.itemgetter(2)) 

　　sorted函数也可以进行多级排序，例如要根据第二个域和第三个域进行排序，可以这么写：

　　sorted(students, key=operator.itemgetter(1,2)) 

（4）reverse参数就不用多说了，是一个bool变量，默认为false（升序排列），定义为True时将按降序排列。

 

sklearn方法

KNeighborsClassifier是一个类，它集成了其他的NeighborsBase, KNeighborsMixin,SupervisedIntegerMixin, ClassifierMixin。

__init__()

初始化函数(构造函数) 它主要有一下几个参数：

n_neighbors=5           int 型参数，knn算法中指定以最近的几个最近邻样本具有投票权，默认参数为5

weights='uniform'       str参数，即每个拥有投票权的样本是按什么比重投票，'uniform'表示等比重投票，'distance'表示按距离反比投票，[callable]表示自己定义的一个函数， 这个函数接收一个距离数组，返回一个权值数组。默认参数为‘uniform’

algrithm='auto'           str参数，即内部采用什么算法实现。有以下几种选择参数：'ball_tree':球树、'kd_tree':kd树、'brute':暴力搜索、'auto':自动根据数据的类型和结构选择合适的算法。默认情况下是‘auto’。暴力搜索就不用说了大家都知道。具体前两种树型数据结构哪种好视情况而定。KD树是对依次对K维坐标轴，以中值切分构造的树,每一个节点是一个超矩形，在维数小于20时效率最高--可以参看《统计学习方法》第二章。ball tree 是为了克服KD树高维失效而发明的，其构造过程是以质心C和半径r分割样本空间，每一个节点是一个超球体。一般低维数据用kd_tree速度快，用ball_tree相对较慢。超过20维之后的高维数据用kd_tree效果反而不佳，而ball_tree效果要好，具体构造过程及优劣势的理论大家有兴趣可以去具体学习。

leaf_size=30               int参数，基于以上介绍的算法，此参数给出了kd_tree或者ball_tree叶节点规模，叶节点的不同规模会影响数的构造和搜索速度，同样会影响储树的内存的大小。具体最优规模是多少视情况而定。

matric='minkowski'     str或者距离度量对象，即怎样度量距离。默认是闵氏距离，闵氏距离不是一种具体的距离度量方法，它可以说包括了其他距离度量方式，是其他距离度量的推广，具体各种距离度量只是参数p的取值不同或者是否去极限的不同情况，具体大家可以参考这里，讲的非常详细。　　　　　　　　　　　　　　　　　　　　　　　　

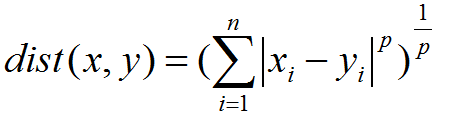
　　p=2                         int参数          就是以上闵氏距离各种不同的距离参数，默认为2，即欧氏距离。p=1代表曼哈顿距离等等

　　metric_params=None                距离度量函数的额外关键字参数，一般不用管，默认为None

　　n_jobs=1                int参数       指并行计算的线程数量，默认为1表示一个线程，为-1的话表示为CPU的内核数，也可以指定为其他数量的线程，这里不是很追求速度的话不用管，需要用到的话去看看多线程。

.fit(traindata，trainlabels)

训练函数，它是最主要的函数。参数：训练数据集和标签集，其实该函数并不是KNeighborsClassifier这个类的方法，而是它的父类SupervisedIntegerMixin继承下来的方法。

.predict(testdata)

预测函数   接收输入的数组类型测试样本，一般是二维数组，每一行是一个样本，每一列是一个属性返回数组类型的预测结果，如果每个样本只有一个输出，则输出为一个一维数组。如果每个样本的输出是多维的，则输出二维数组，每一行是一个样本，每一列是一维输出。

predict_prob(testdata)

基于概率的软判决，也是预测函数，只是并不是给出某一个样本的输出是哪一个值，而是给出该输出是各种可能值的概率各是多少接收参数和上面一样返回参数和上面类似，只是上面该是值的地方全部替换成概率，比如说输出结果又两种选择0或者1，上面的预测函数给出的是长为n的一维数组，代表各样本一次的输出是0还是1.而如果用概率预测函数的话，返回的是n*2的二维数组，每一行代表一个样本，每一行有两个数，分别是该样本输出为0的概率为多少，输出1的概率为多少。而各种可能的顺序是按字典顺序排列，比如先0后1，或者其他情况等等都是按字典顺序排列。

score(testdata，reallabel，weigh)

计算准确率的函数，接受参数有3个。 X:接收输入的数组类型测试样本，一般是二维数组，每一行是一个样本，每一列是一个属性。y:X这些预测样本的真实标签，一维数组或者二维数组。sample_weight=None,是一个和X第一位一样长的各样本对准确率影响的权重，一般默认为None.输出为一个float型数，表示准确率。内部计算是按照predict()函数计算的结果记性计算的。其实该函数并不是KNeighborsClassifier这个类的方法，而是它的父类KNeighborsMixin继承下来的方法。

kneighbors(目标样本，临近样本数量，是否返回距离值)

计算某些测试样本的最近的几个近邻训练样本。接收3个参数。X=None：需要寻找最近邻的目标样本。n_neighbors=None,表示需要寻找目标样本最近的几个最近邻样本，默认为None,需要调用时给出。return_distance=True:是否需要同时返回具体的距离值。返回最近邻的样本在训练样本中的序号。其实该函数并不是KNeighborsClassifier这个类的方法，而是它的父类KNeighborsMixin继承下来的方法。

sklearn有数据集，需要引入： from sklearn import datasets