信息在DNN马尔科夫链结构上的变化

一个经典的全连接神经网络，如下图所示，输入层可以看做T₀，输出层可以看做$\hat{\mathrm{Y}}$=T_L+1。

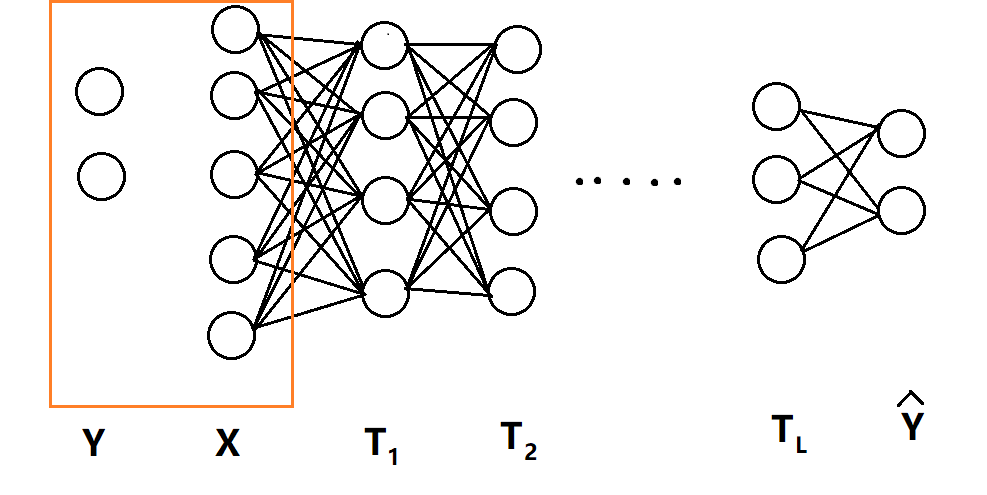
考虑每一层隐藏层T与X、Y的交互信息：I(X; T_i), I(T_i, Y)，交互信息部分的知识参见上一篇文章

在训练过程中每一轮把这两个交互信息画出来，横轴I(X; T_i)，纵轴I(T_i, Y)，同一颜色多个点代表同一层内多个神经元，不同颜色的点代表不同层数的神经元：

round 0-160：I(T_i, Y)快速上升，I(X; T_i)也随之增加

round 170-410: I(T_i, Y)继续上升，I(X; T_i)增加到一定程度之后，开始集体掉头减少。

round 420-1600：所有神经元开始集体往高I(T_i, Y)，低I(X; T_i)的左上角移动

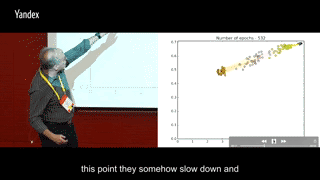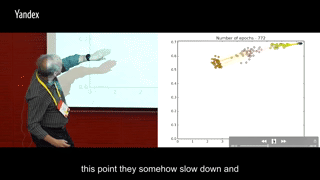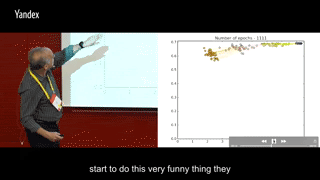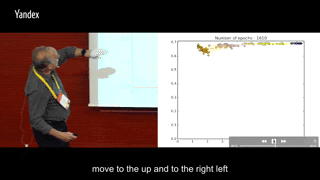
round 1600-5000：I(T_i, Y)保持稳定，训练到后面或许会有少许下滑，同时I(X; T_i)继续减少。

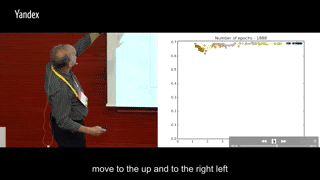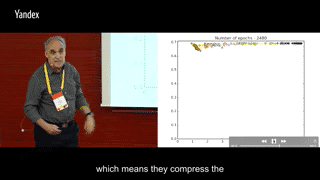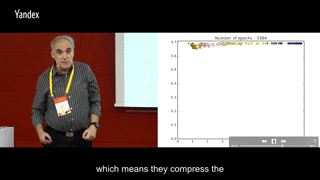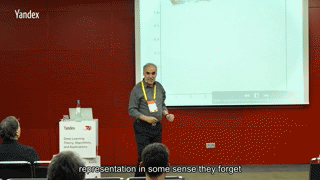
上面的交互信息变化是一个典型的全连接分类问题训练时画出的，而且并没有使用两层之间特征向量的交互信息，而是使用了两层之间神经元的交互信息，估计是向量的排列组合数远大于神经元的可能数值数量，不方便统计概率。所以转而使用两层之间神经元两两之间的交互信息，再以此近似两层特征向量之间的交互信息。

看图的时候，自动脑补同一颜色的所有点聚类之后得到的中心位置，就能想象出两层之间特征向量交互信息的移动轨迹了。

可以很明显地发现两个阶段：第一阶段I(T_i, Y)与I(X; T_i)一起上升，第二阶段I(T_i, Y)继续上升但I(X; T_i)下降。第一阶段很快就能走完，第二阶段要迭代比第一阶段多出很多次，才能最终完成收敛。

接下来要分析I(T_i, Y)增加的原因：

首先定义信息瓶颈扭曲(information bottleneck distortion)这个概念：

$d_{IB}(x,t)=D_{KL}\left(p(y\mid x)\parallel p(y\mid t)\right)=\sum\limits _{y}p(y\mid x)log\frac{p(y\mid x)}{p(y\mid t)}$

我们希望当训练完成之后，无论是用完整的网络输入x，还是把网络从中间砍开，在中间输入特征值t，二者最终输出的y都是接近的。因为不同层的特征值代表不同抽象等级的同一个输入，好比我们希望从矿石、橡胶等料经过全流程加工得到的汽车，与从轮胎、车架、座椅等中间件开始半路组装得到的汽车，最终产出是一致的。

考虑上式的预期值，并简化：

$E\left[d_{IB}\right]=\sum\limits _{x,t}p(x)p(t)d_{IB}(x,t)$

$=\sum\limits _{x,t,y}p(x)p(t)p(y\mid x)logp(y\mid x)-\sum\limits _{x,t,y}p(x)p(t)p(y|x)logp(y\mid t)$

使用$p(y\mid t)=\sum\limits _{x}p(y\mid x)p(x\mid t)$带入

$=-\sum\limits _{x,t}p(x)p(t)H(Y\mid x)-\sum\limits _{t,y}\frac{p(x)p(t)}{p(x\mid t)}p(y\mid t)logp(y\mid t)$

$=-\sum\limits _{x,{\color{red}t}}p(x){\color{red}{p(t)}}H(Y\mid x)+\sum\limits _{{\color{red}t}}\frac{{\color{red}{p(x)}}p(t)}{{\color{red}{p(x\mid t)}}}H(Y\mid t)$

$=-H(Y\mid X)+H(Y\mid T)$

使用交互信息$I(A;B)=H(A)-H(A\mid B)$

$E\left[d_{IB}\right]=I(X;Y)-I(T;Y)$

左边大于0，右边I(X;Y)是样本决定的，与网络结构无关，当做常量，所以要想让左边尽量小，需要让I(T;Y)尽量大。

所以我们会看到随着训练过程的进行，I(T;Y)基本上会一直增加，目的就是为了让神经网络结构无论从哪一层独立获得正确的输入时，输出都是一致的。

这里T选取的是任意一层隐藏层的特征值。在T₀=X层情况下，左边恒等0，I(T;Y)取最大值I(X;Y)。在T_L+1层情况下，I(T;Y)取值I($\hat{\mathrm{Y}}$;Y)。

在最初网络权重全部随机值的时候，I($\hat{\mathrm{Y}}$;Y)基本为0，随着层数i从0逐渐增加到L+1，I(T_i;Y)逐渐减少。我们可以从gif动图上最初round 0看出这个现象。

I(X; T_i)先增加再减小的原理有些复杂，一般把减小的过程叫做压缩，在一部分网络结构里会出现压缩现象，而在另一部分网络结构里，压缩现象并不明显。推测是与样本数量与使用的激活函数有关。

下一篇文章将会着重分析为什么会出现压缩，以及压缩的作用。