bzoj3283: 运算器

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 using namespace std;
 typedef long long int64;
 int Case;
 #define maxn 200005
 #define maxm 600005
 int now[maxn],prep[maxm];
 int64 val[maxm],pi,pk,t;
 int64 ksm(int64 x,int64 y,int64 p){
     if (y==) return %p;
     if (y==) return x%p;
     int64 d=ksm(x,y/,p);
     if (y%==) return d*d%p*x%p;
     else return d*d%p;
 }
 int64 exgcd(int64 a,int64 b,int64 &x,int64 &y){
     if (b==){
         x=,y=;
         return a;
     }
     int64 GCD=exgcd(b,a%b,x,y),temp;
     temp=x,x=y,y=temp-a/b*y;
     return GCD;
 }
 void insert(int x,int64 y){
     int pos=y%maxn;
     prep[x]=now[pos],now[pos]=x,val[x]=y;
 }
 int search(int64 x){
     int pos=x%maxn,ans=maxm*;
     for (int i=now[pos];i!=-;i=prep[i]){
         if (val[i]==x) ans=min(ans,i);
     }
     if (ans<maxm*) return ans;
     else return -;
 }
 int64 extanded_baby_step_gaint_step(int64 A,int64 B,int64 C){
     int64 tmp,temp=,x,y,D,R,cnt=; int pos;
     for (int i=;i<;i++){
         if (temp==B) return i;
         temp=temp*A%C;
     }
     D=;
     for (temp=exgcd(A,C,x,y);temp!=;cnt++,temp=exgcd(A,C,x,y)){
         if (B%temp) return -;
         C/=temp,B/=temp;
         D=D*(A/temp)%C;
     }
     memset(now,-,sizeof(now));
     R=; tmp=ceil(sqrt(C*1.0));
     for (int i=;i<tmp;i++){
         insert(i,R);
         R=R*A%C;
     }
     for (int i=;i<tmp;i++){
         temp=exgcd(D,C,x,y);
         x=(x%C*(B/temp)%C+C)%C;
         pos=search(x);
         if (pos!=-) return i*tmp+pos+cnt;
         D=D*R%C;
     }
     return -;
 }
 int64 inv(int64 X){
     int64 x,y;
     int64 temp=exgcd(X,pk,x,y);
     return (x%pk+pk)%pk;
 }
 int64 work(int64 n){
     if (n==) return 1LL%pk;
     int64 ans=;
     for (int i=;i<=pk;i++) if (i%pi) ans=ans*i%pk;
     ans=ksm(ans,n/pk,pk);
     int64 k=n%pk;
     for (int i=;i<=k;i++) if (i%pi) ans=ans*i%pk;
     return ans*work(n/pi)%pk;
 }
 int64 calc(int64 n,int64 m){
     int64 a,b,c; int64 k=;
     a=work(n),b=work(n-m),c=work(m);
     for (int i=n;i;i/=pi) k+=(i/pi);
     for (int i=n-m;i;i/=pi) k-=(i/pi);
     for (int i=m;i;i/=pi) k-=(i/pi);
     return 1LL*ksm(pi,k,pk)%pk*a%pk*inv(b)%pk*inv(c)%pk;
 }
 void work1(){
     int64 n,m,p;
     scanf("%lld%lld%lld",&n,&m,&p);
     printf("%lld\n",ksm(n,m,p)%p);
 }
 void work2(){
     int64 A,B,C,ans;
     scanf("%lld%lld%lld",&A,&B,&C);
     B%=C;
     ans=extanded_baby_step_gaint_step(A,B,C);
     if (ans==-) printf("Math Error\n");
     else printf("%lld\n",ans);
 }
 void work3(){
     int64 n,m,p,temp,x,y,tmp,ans=;
     scanf("%lld%lld%lld",&m,&n,&p);
     t=p;
     for (int i=;i<=sqrt(p);i++){
         if (t%i==){
             pi=i,pk=;
             while (t%i==){
                 pk=pk*i;
                 t/=i;
             }
             temp=exgcd(p/pk,pk,x,y);
             tmp=calc(n,m)/temp;
             x=x*tmp%p*(p/pk)%p;
             ans=(ans+x)%p;
         }
     }
     if (t>){
         pi=t,pk=t;
         temp=exgcd(p/pk,pk,x,y);
         tmp=calc(n,m)/temp;
         x=x*tmp%p*(p/pk)%p;
         ans=(ans+x)%p;
     }
     printf("%lld\n",(ans%p+p)%p);
 }
 int main(){
     scanf("%d",&Case);
     for (int type;Case;Case--){
         scanf("%d",&type);
         if (type==) work1();
         else if (type==) work2();
         else work3();
     }
     return ;
 }

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=3283

题目大意：

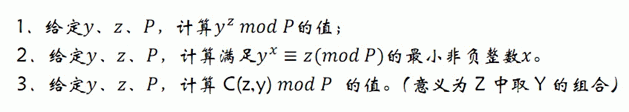
吐槽：HN2016省队集训原题，辣鸡出题人......

做法：对于操作1，没什么好说的，直接上快速幂即可。

对于操作2，如果p是质数，就是BSGS算法，否则，就用扩展BSGS算法；而实际上扩展BSGS可以解决p是质数，所以就不用分类讨论了。

对于（extended)baby_step_gaint_step算法，未完待续......

对于操作3，组合数取模，扩展lucas定理。

对于组合数取模，未完待续......