CF467C George and Job (DP)
Codeforces Round #267 (Div. 2)
|
C. George and Job
time limit per test
1 second memory limit per test
256 megabytes input
standard input output
standard output The new ITone 6 has been released recently and George got really keen to buy it. Unfortunately, he didn't have enough money, so George was going to work as a programmer. Now he faced the following problem at the work. Given a sequence of n integers p1, p2, ..., pn. You are to choose k pairs of integers: [l1, r1], [l2, r2], ..., [lk, rk] (1 ≤ l1 ≤ r1 < l2 ≤ r2 < ... < lk ≤ rk ≤ n; ri - li + 1 = m), in such a way that the value of sum Input
The first line contains three integers n, m and k (1 ≤ (m × k) ≤ n ≤ 5000). The second line contains n integers p1, p2, ..., pn (0 ≤ pi ≤ 109). Output
Print an integer in a single line — the maximum possible value of sum. Sample test(s)
Input
5 2 1 Output
9 Input
7 1 3 Output
61 |
题意:
给出n,m,k,给出由n个数组成的序列,在其中选出k组不重叠的连续m个数,使选择的数的和最大。
题解:
DP。
f[i][j],表示在[1,i]中选了j个区间得到的最大的和。
由于要经常求某连续m个数的和,可以先预处理出所有连续m个数的和,sum[i]表示以i为结尾的连续m个数的和。
最后结果为f[n][k]。
状态转移:
mf1(f);///全部置为-1
FOR(i,,n) f[i][]=;
FOR(i,,n){
FOR(j,,k){
f[i][j]=f[i-][j];
if(i-m>= && f[i-m][j-] != -) f[i][j]=max(f[i][j],f[i-m][j-]+sum[i]);
}
}
全代码:
//#pragma comment(linker, "/STACK:102400000,102400000")
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<set>
#include<stack>
#include<queue>
using namespace std;
#define ll long long
#define usll unsigned ll
#define mz(array) memset(array, 0, sizeof(array))
#define mf1(array) memset(array, -1, sizeof(array))
#define minf(array) memset(array, 0x3f, sizeof(array))
#define REP(i,n) for(i=0;i<(n);i++)
#define FOR(i,x,n) for(i=(x);i<=(n);i++)
#define RD(x) scanf("%d",&x)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define WN(x) printf("%d\n",x);
#define RE freopen("D.in","r",stdin)
#define WE freopen("1biao.out","w",stdout)
#define mp make_pair
#define pb push_back
const double eps=1e-;
const double pi=acos(-1.0);
int a[];
ll sum[];
ll f[][];///f[i][j],到i时选了j个区间
int n,m,k;
int main(){
int i,j;
RD3(n,m,k);
FOR(i,,n){
RD(a[i]);
}
ll sm=;
FOR(i,,n){
sm+=a[i];
if(i>=m){
sum[i]=sm;
sm-=a[i-m+];
}
}
mf1(f);///全部置为-1
FOR(i,,n) f[i][]=;
FOR(i,,n){
FOR(j,,k){
f[i][j]=f[i-][j];
if(i-m>= && f[i-m][j-] != -) f[i][j]=max(f[i][j],f[i-m][j-]+sum[i]);
}
}
printf("%I64d\n",f[n][k]);
return ;
}
CF467C George and Job (DP)的更多相关文章
- Codeforces Round #267 (Div. 2) C. George and Job (dp)
wa哭了,,t哭了,,还是看了题解... 8170436 2014-10-11 06:41:51 njczy2010 C - George and Jo ...
- Codeforces 467C George and Job(DP)
题目 Source http://codeforces.com/contest/467/problem/C Description The new ITone 6 has been released ...
- Codeforces Round #267 (Div. 2) C. George and Job(DP)补题
Codeforces Round #267 (Div. 2) C. George and Job题目链接请点击~ The new ITone 6 has been released recently ...
- codeforces #267 C George and Job(DP)
职务地址:http://codeforces.com/contest/467/problem/C 太弱了..这题当时都没做出来..思路是有的,可是自己出的几组数组总是过不去..今天又又一次写了一遍.才 ...
- 【Codeforces】CF 467 C George and Job(dp)
题目 传送门:QWQ 分析 dp基础题. $ dp[i][j] $表示前i个数分成j组的最大和. 转移显然. 吐槽:做cf题全靠洛谷翻译苟活. 代码 #include <bits/stdc++. ...
- LightOJ 1033 Generating Palindromes(dp)
LightOJ 1033 Generating Palindromes(dp) 题目链接:http://acm.hust.edu.cn/vjudge/contest/view.action?cid= ...
- lightOJ 1047 Neighbor House (DP)
lightOJ 1047 Neighbor House (DP) 题目链接:http://acm.hust.edu.cn/vjudge/contest/view.action?cid=87730# ...
- UVA11125 - Arrange Some Marbles(dp)
UVA11125 - Arrange Some Marbles(dp) option=com_onlinejudge&Itemid=8&category=24&page=sho ...
- 【POJ 3071】 Football(DP)
[POJ 3071] Football(DP) Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 4350 Accepted ...
随机推荐
- Leetcode 134 Gas Station
There are N gas stations along a circular route, where the amount of gas at station i is gas[i]. You ...
- kali 2.0 启动metasploit服务
kali 2.0 已经没有metasploit 这个服务了,所以service metasploit start 的方式不起作用. 在kali 2.0中启动带数据库支持的MSF方式如下: 首先启动po ...
- CVE-2015-1328 Ubuntu 12.04, 14.04, 14.10, 15.04 overlayfs Local Root
catalog . 引言 . Description . Effected Scope . Exploit Analysis . Principle Of Vulnerability . Patch ...
- luars232库中用到的一些C API for lua
代码就不贴了,这里只是梳理一下前两篇里面忽略的一些东西,作为读代码的记录吧. 1.头文件 #include <lauxlib.h> #include <lua.h> All A ...
- Python脚本运行出现语法错误:IndentationError: unindent does not match any outer indentation level
运行环境是win7 x64 sublime text2,百度发现是对齐问题. 具体来说是由于有的地方使用了4个空格,有的地方使用了tab键. 代码区直接全选就会看到有的地方是四个点有个地方是一个横线, ...
- oracle修改表字段名时报错:ORA-00054:资源正忙,但指定以NOWAIT方式获取资源,或者超时失效的问题
打开sql plus select session_id from v$locked_object;查询出oracle锁定的会话ID SELECT sid, serial#, username, os ...
- bootstrap学习总结-05 常用标签3
1 单选框,多选框 1)单选框 单选框(radio)用于从多个选项中只选择一个.设置了 disabled 属性的单选或多选框都能被赋予合适的样式.对于和多选或单选框联合使用的 <label> ...
- Rsync
转自:http://www.mike.org.cn/blog/index.php?load=read&id=639###pp=0 [rsync实现网站的备份,文件的同步,不同系统的文件的同步, ...
- java常用集合详解 contains
java集合是对常用数据集合的封装,差不多就是数组吧,验证某个元素是否在数据集合里,最原始的方法是,用个循环,"某个元素"与数据集合中的每个元素逐个进行比较. java 对常用的一 ...
- 数组Arrays
1.toString 方法 Arrays的toString方法可以方便的输出一个数组的字符串形式,方便查看,它有九个重载的方法,包括八种基本类型数组和一个对象类型数组,这里列举两个: public s ...

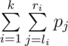 is maximal possible. Help George to cope with the task.
is maximal possible. Help George to cope with the task.