POJ 1905 Expanding Rods

                       Expanding Rods

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 10187		Accepted: 2593

Description

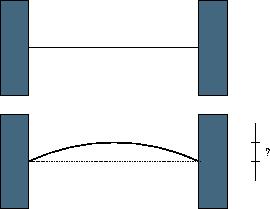
When a thin rod of length L is heated n degrees, it expands to a new length L'=(1+n*C)*L, where C is the coefficient of heat expansion. 
When a thin rod is mounted on two solid walls and then heated, it expands and takes the shape of a circular segment, the original rod being the chord of the segment.

Your task is to compute the distance by which the center of the rod is displaced.

Input

The input contains multiple lines. Each line of input contains three non-negative numbers: the initial lenth of the rod in millimeters, the temperature change in degrees and the coefficient of heat expansion of the material. Input data guarantee that no rod expands by more than one half of its original length. The last line of input contains three negative numbers and it should not be processed.

Output

For each line of input, output one line with the displacement of the center of the rod in millimeters with 3 digits of precision. 

Sample Input

1000 100 0.0001

15000 10 0.00006

10 0 0.001

-1 -1 -1

Sample Output

61.329
225.020
0.000

Source

Waterloo local 2004.06.12

我们要求的是下图中的b，显然b的取值范围是[0，L/2]。对于每一个b，我们可以求出在已知弦L的情况下的半径R，从而可以求出此半径R和弦L下对应的圆弧的长度L0。经过与公式计算出来的L1进行对比，调整b的大小。经过观察，发现b越大，L0也就越大。所以如果L0>L1，应使b减小（right=mid-e），以减少L0。相反，当L0<L1的时候，应该让b增大（left=mid+e），以增大L0。

附注：求半径的方法是根据a,b,d，先求出h，然后求出R。接着根据圆心角和半径，求出圆弧的长度。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>

 using namespace std;

 const double eps=1e-;

 double l,l0,l00;

 double get00(double b)
 {
     double a=l/.;
     double d=sqrt(a*a+b*b);
     double h=d*a/b;
     double R=sqrt(h*h+d*d)/.;
     double alpha=atan(b/a);
     return *alpha*R;
 }

 int main()
 {
     double n,c;
     while(cin>>l>>n>>c)
     {
         if(l<&&n<&&c<) break;
         l0=(.+n*c)*l;
         if(fabs(l0-l)<eps)
         {
             printf("0.000\n");
             continue;
         }
         double low=,high=l/.,mid,ans;
         while(low<high)
         {
             mid=(low+high)/.;
             l00=get00(mid);
             if(fabs(l00-l0)<eps)
             {
                 ans=mid; break;
             }
             else if(l00>l0)
                 high=mid;
             else
                 low=mid;
         }
         printf("%.3lf\n",ans);
     }
     return ;
 }