POJ 3164 Command Network 最小树形图 朱刘算法

=============== 分割线之下摘自Sasuke_SCUT的blog=============

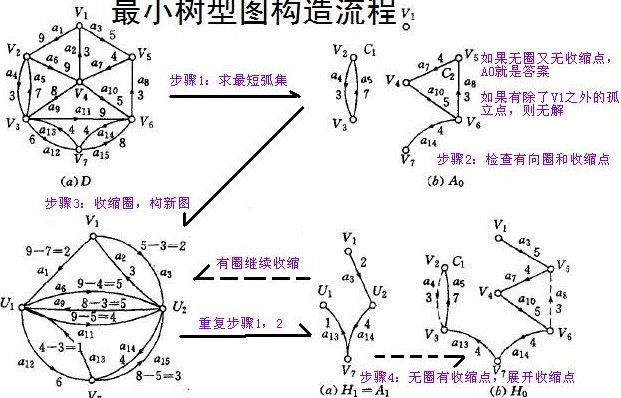
最 小树形图，就是给有向带权图中指定一个特殊的点root，求一棵以root为根的有向生成树T，并且T中所有边的总权值最小。最小树形图的第一个算法是 1965年朱永津和刘振宏提出的复杂度为O(VE)的算法。 判断是否存在树形图的方法很简单，只需要以v为根作一次图的遍历就可以了，所以下面的 算法中不再考虑树形图不存在的情况。 在所有操作开始之前，我们需要把图中所有的自环全都清除。很明显，自环是不可能在任何一个树形图上的。只有进 行了这步操作，总算法复杂度才真正能保证是O(VE)。 首先为除根之外的每个点选定一条入边，这条入边一定要是所有入边中最小的。现在所有的最小 入边都选择出来了，如果这个入边集不存在有向环的话，我们可以证明这个集合就是该图的最小树形图。这个证明并不是很难。如果存在有向环的话，我们就要将这 个有向环所称一个人工顶点，同时改变图中边的权。假设某点u在该环上，并设这个环中指向u的边权是in[u]，那么对于每条从u出发的边(u, i, w)，在新图中连接(new, i, w)的边，其中new为新加的人工顶点; 对于每条进入u的边(i, u, w)，在新图中建立边(i, new, w-in[u])的边。为什么入边的权要减去in[u]，这个后面会解释，在这里先给出算法的步骤。然后可以证明，新图中最小树形图的权加上旧图中被收缩 的那个环的权和，就是原图中最小树形图的权。 上面结论也不做证明了。现在依据上面的结论，说明一下为什么出边的权不变，入边的权要减去in [u]。对于新图中的最小树形图T，设指向人工节点的边为e。将人工节点展开以后，e指向了一个环。假设原先e是指向u的，这个时候我们将环上指向u的边 in[u]删除，这样就得到了原图中的一个树形图。我们会发现，如果新图中e的权w'(e)是原图中e的权w(e)减去in[u]权的话，那么在我们删除 掉in[u]，并且将e恢复为原图状态的时候，这个树形图的权仍然是新图树形图的权加环的权，而这个权值正是最小树形图的权值。所以在展开节点之后，我们 得到的仍然是最小树形图。逐步展开所有的人工节点，就会得到初始图的最小树形图了。 如果实现得很聪明的话，可以达到找最小入边O(E)，找环 O(V)，收缩O(E)，其中在找环O(V)这里需要一点技巧。这样每次收缩的复杂度是O(E)，然后最多会收缩几次呢？由于我们一开始已经拿掉了所有的 自环，我门可以知道每个环至少包含2个点，收缩成1个点之后，总点数减少了至少1。当整个图收缩到只有1个点的时候，最小树形图就不不用求了。所以我们最 多只会进行V-1次的收缩，所以总得复杂度自然是O(VE)了。由此可见，如果一开始不除去自环的话，理论复杂度会和自环的数目有关。

======================== 分割线之上摘自Sasuke_SCUT的blog=====================================================
下 面是朱刘算法的构造图

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn = 110;
const double inf = 1e10;
struct point{
    double x,y;
}arr[maxn];
struct node{
    int u,v;
    double cost;
}edge[maxn*maxn*10];
int vis[maxn],pre[maxn],ID[maxn];
double in[maxn];
int n,m;
double lenth(point a,point b){
    return sqrt(pow(a.x-b.x,2) + pow(a.y-b.y,2));
}
double zhu_liu(int root){
	int i,u,v;
    double ans = 0;
    while( 1 ){
        for( i = 0; i < n; i++)in[i] = inf;
        //1.找最小边
        for( i = 0; i < m; i++){
             u = edge[i].u;
             v = edge[i].v;
            if( edge[i].cost > in[v] || u == v)continue;
            in[v] = edge[i].cost;
            pre[v] = u;
        }
        for( i = 0; i < n; i++)//当存在除了根外还有不可达的点时，返回-1
            if( root != i &&  in[i] == inf)return -1;

        int cntnode = 0;
        memset(vis,-1,sizeof(vis));
        memset(ID,-1,sizeof(ID));
        in[root] = 0;
        //2.找环
        for( i = 0; i < n; i++){
            ans += in[i];
             v = i;
            while( vis[v] != i && ID[v] == -1 && v != root){
                vis[v] = i;
                v = pre[v];
            }
            if( v != root && ID[v] == -1){
                for( u = pre[v]; u != v; u = pre[u])
                ID[u] = cntnode;
                ID[v] = cntnode++;
            }
        }
        if( cntnode == 0)break;//不存在环，则结束循环
        //3.缩点和重标记
        for( i = 0; i < n; i++)
        if( ID[i] == -1)ID[i] = cntnode++;
        for( i = 0; i < m; i++){
           int u = edge[i].u,v = edge[i].v;
            edge[i].u = ID[u];
            edge[i].v = ID[v];
            if( edge[i].u != edge[i].v)
            edge[i].cost -= in[v];
        }
        n = cntnode;
        root = ID[root];
    }
    return ans;
}
int main(){
	int i;
    //freopen("in.txt","r",stdin);
    while(~scanf("%d%d",&n,&m)){
        for( i = 0; i < n; i++)
        scanf("%lf%lf",&arr[i].x,&arr[i].y);
        for( i = 0; i < m; i++){
            scanf("%d%d",&edge[i].u,&edge[i].v);
            edge[i].u--;edge[i].v--;
            if(edge[i].u == edge[i].v)
            edge[i].cost = inf;
            else edge[i].cost = lenth(arr[edge[i].u],arr[edge[i].v]);
        }
        double ans = zhu_liu(0);
        if( ans == -1)puts("poor snoopy");
        else printf("%.2lf\n",ans);
    }
    return 0;
}